So führen sie eine logistische regression in spss durch

Die logistische Regression ist eine Methode, mit der wir ein Regressionsmodell anpassen, wenn die Antwortvariable binär ist.

In diesem Tutorial wird erläutert, wie Sie eine logistische Regression in SPSS durchführen.

Beispiel: Logistische Regression in SPSS

Führen Sie die folgenden Schritte aus, um in SPSS eine logistische Regression für einen Datensatz durchzuführen, der angibt, ob College-Basketballspieler basierend auf ihrem GPA in die NBA eingezogen wurden (Draft: 0 = Nein, 1 = Ja). Punkte pro Spiel und ihre Divisionsstufe.

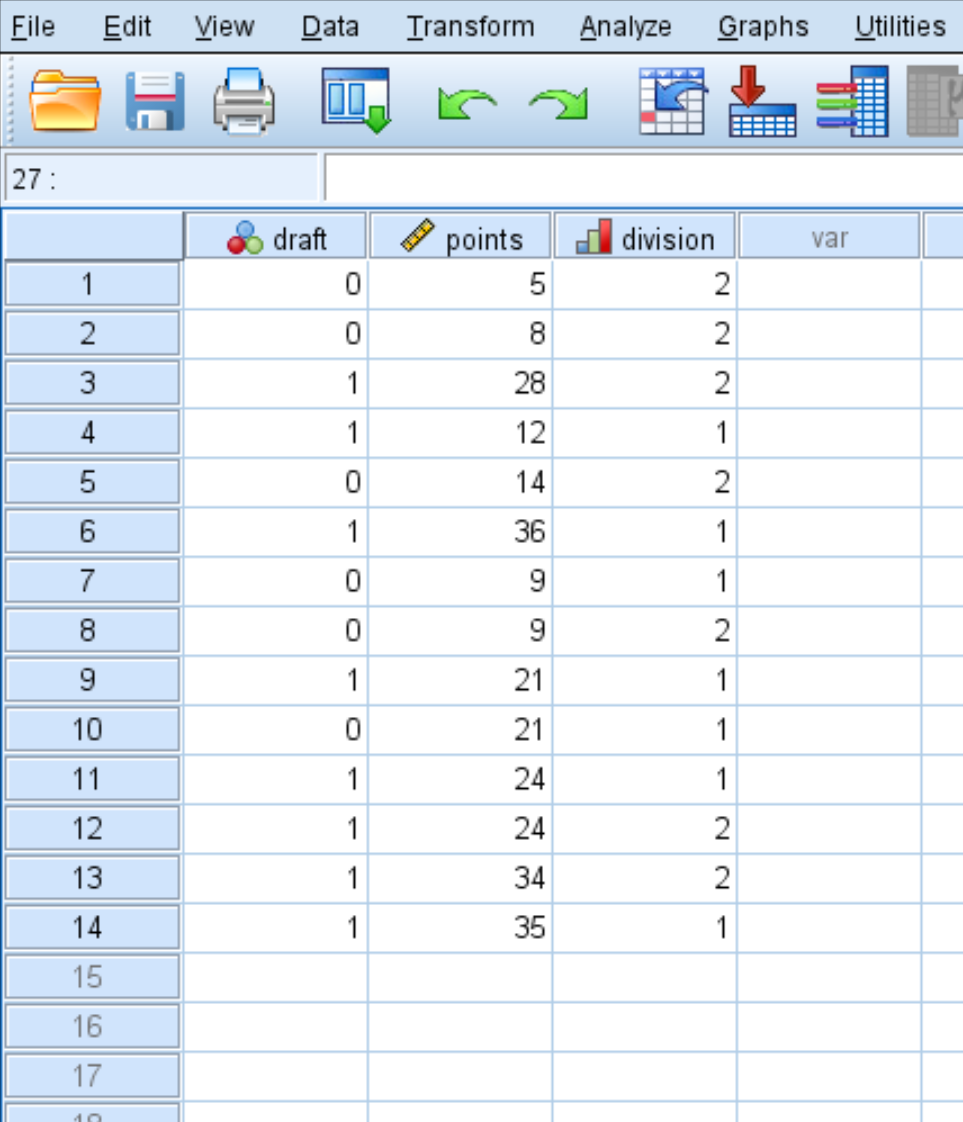
Schritt 1: Geben Sie die Daten ein.

Geben Sie zunächst folgende Daten ein:

Schritt 2: Führen Sie eine logistische Regression durch.

Klicken Sie auf die Registerkarte „Analysieren“ , dann auf „Regression“ und dann auf „Binary Logistic Regression“ :

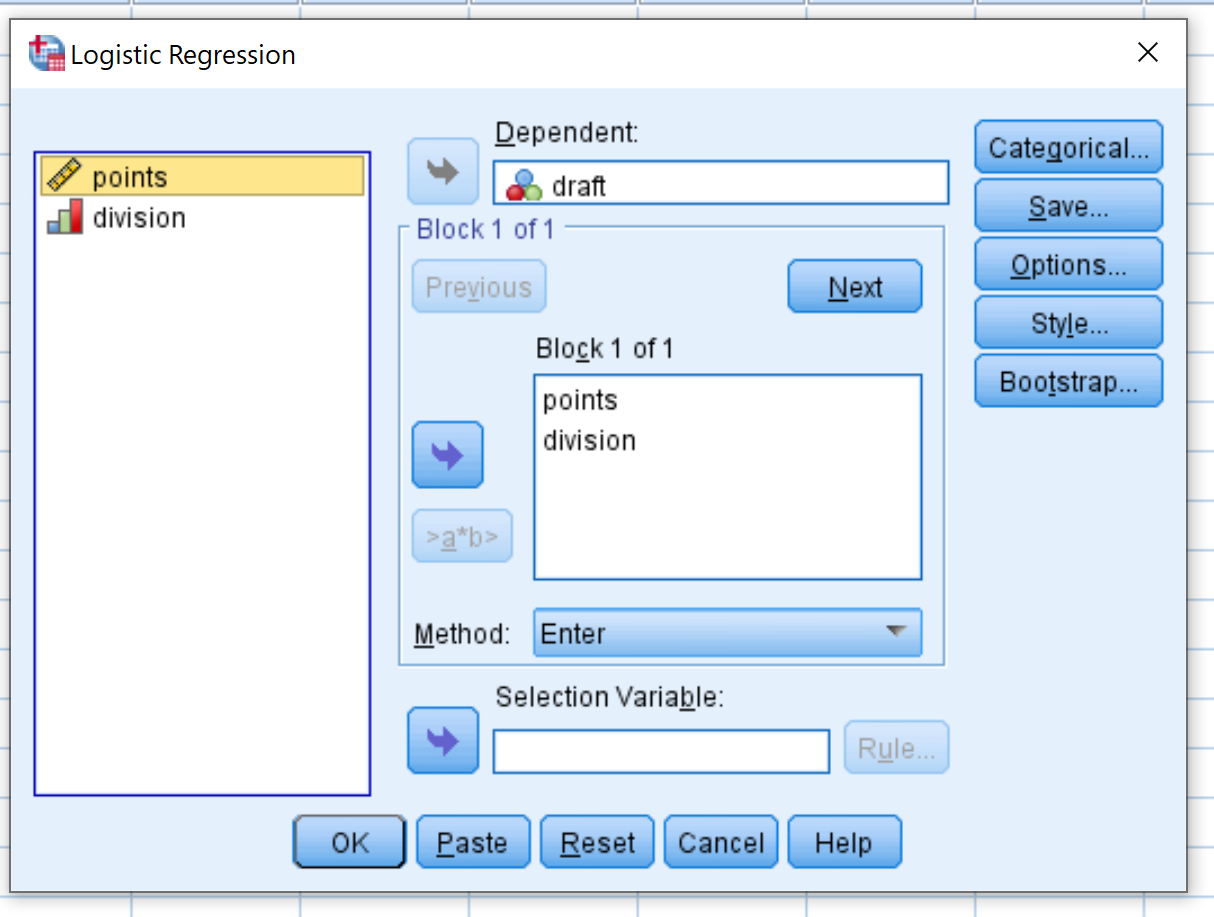
Ziehen Sie im neuen Fenster, das erscheint, das Projekt der binären Antwortvariablen in den Bereich mit der Bezeichnung „Abhängig“. Ziehen Sie dann den Doppelpunkt und die Division der Prädiktorvariablen in das Feld mit der Bezeichnung „Block 1 von 1“. Lassen Sie die Methode auf „Eingabe“ eingestellt. Klicken Sie dann auf OK .

Schritt 3. Interpretieren Sie das Ergebnis.

Sobald Sie auf OK klicken, wird das Ergebnis der logistischen Regression angezeigt:

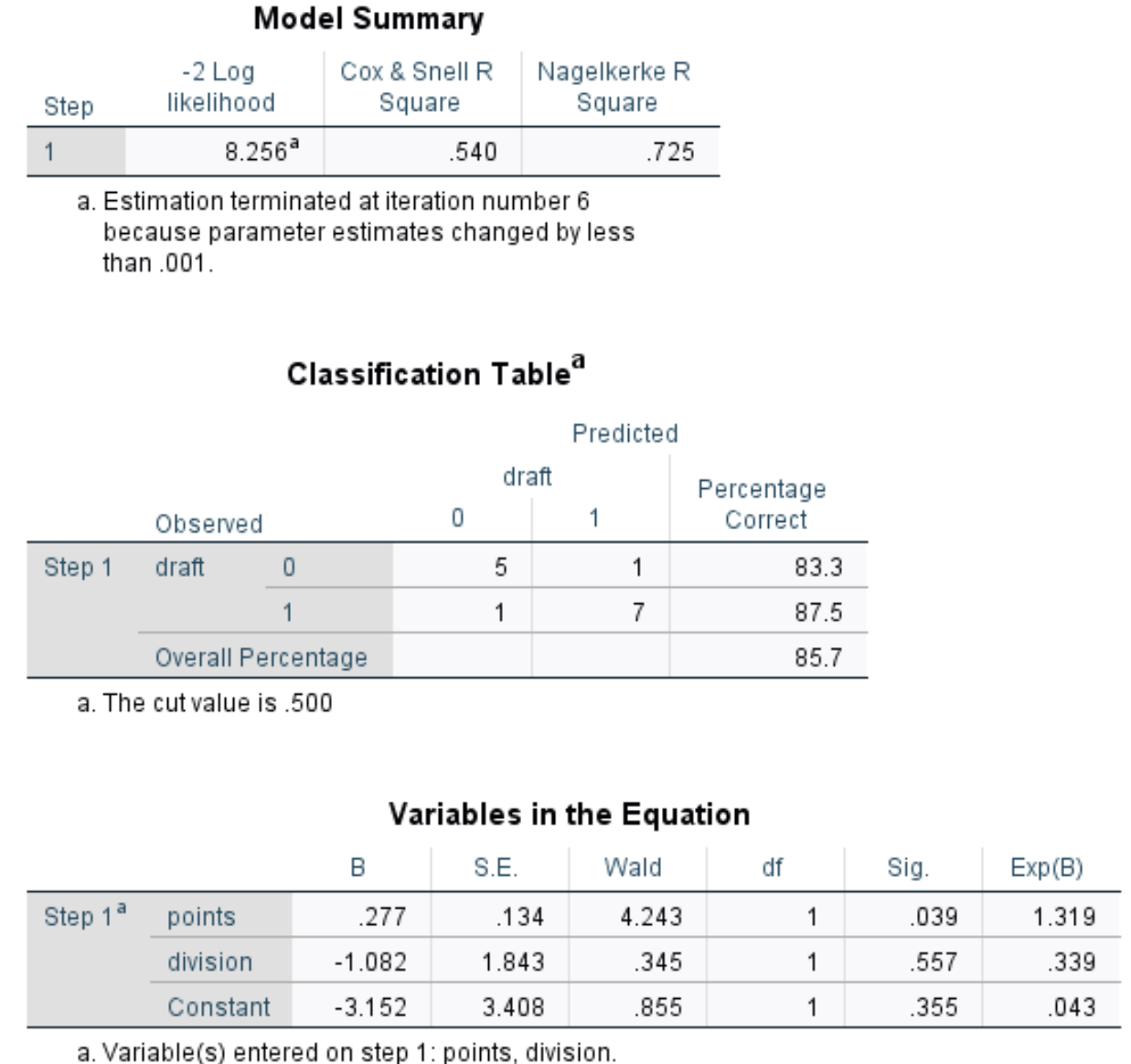
So interpretieren Sie das Ergebnis:

Modellzusammenfassung: Die nützlichste Metrik in dieser Tabelle ist das Nagelkerke-R-Quadrat, das uns den Prozentsatz der Variation in der Antwortvariablen angibt, der durch die Prädiktorvariablen erklärt werden kann. In diesem Fall können Punkte und Division 72,5 % der Entwurfsvariabilität erklären.

Klassifizierungstabelle: Die nützlichste Metrik in dieser Tabelle ist der Gesamtprozentsatz, der uns den Prozentsatz der Beobachtungen angibt, die das Modell korrekt klassifizieren konnte. In diesem Fall konnte das logistische Regressionsmodell das Draft-Ergebnis von 85,7 % der Spieler korrekt vorhersagen.

Variablen in der Gleichung: Diese letzte Tabelle liefert uns mehrere nützliche Messungen, darunter:

• Wald: Wald-Teststatistik für jede Prädiktorvariable, die verwendet wird, um zu bestimmen, ob jede Prädiktorvariable statistisch signifikant ist oder nicht.
• Sig: der p-Wert, der der Wald-Teststatistik für jede Prädiktorvariable entspricht. Wir sehen, dass der p-Wert für Punkte 0,039 und der p-Wert für Division 0,557 beträgt.
• Exp(B): das Quotenverhältnis für jede Prädiktorvariable. Daraus ersehen wir die Veränderung der Wahrscheinlichkeit, dass ein Spieler gedraftet wird, verbunden mit einem Anstieg einer bestimmten Prädiktorvariablen um eine Einheit. Beispielsweise beträgt die Wahrscheinlichkeit, dass ein Spieler der Division 2 gedraftet wird, nur 0,339 der Wahrscheinlichkeit, dass ein Spieler der Division 1 gedraftet wird. Ebenso ist jede zusätzliche Punkterhöhung pro Spiel mit einer Erhöhung der Chancen, dass ein Spieler gedraftet wird, um 1.319 verbunden.

Anschließend können wir die Koeffizienten (die Werte in der mit B gekennzeichneten Spalte) verwenden, um die Wahrscheinlichkeit vorherzusagen, dass ein bestimmter Spieler gedraftet wird, und zwar mithilfe der folgenden Formel:

Wahrscheinlichkeit = e ^{-3,152 + 0,277 (Punkte) – 1,082 (Teilung)} / (1+e ^{-3,152 + 0,277 (Punkte) – 1,082 (Teilung)} )

Beispielsweise kann die Wahrscheinlichkeit, dass ein Spieler, der durchschnittlich 20 Punkte pro Spiel erzielt und in der Division 1 spielt, gedraftet wird, wie folgt berechnet werden:

Wahrscheinlichkeit = e ^{-3,152 + 0,277(20) – 1,082(1)} / (1+e ^{-3,152 + 0,277(20) – 1,082(1)} ) = 0,787 .

Da diese Wahrscheinlichkeit größer als 0,5 ist, würden wir vorhersagen, dass dieser Spieler gedraftet wird.

Schritt 4. Melden Sie die Ergebnisse.

Abschließend möchten wir über die Ergebnisse unserer logistischen Regression berichten. Hier ist ein Beispiel dafür:

Eine logistische Regression wurde durchgeführt, um zu bestimmen, wie sich Punkte pro Spiel und Divisionsstufe auf die Wahrscheinlichkeit eines Basketballspielers auswirken, gedraftet zu werden. Insgesamt wurden 14 Spieler in die Analyse einbezogen.

Das Modell erklärte 72,5 % der Abweichungen im Projektergebnis und klassifizierte 85,7 % der Fälle korrekt.

Die Wahrscheinlichkeit, dass ein Spieler der Division 2 gedraftet wird, betrug nur 0,339 der Wahrscheinlichkeit, dass ein Spieler der Division 1 gedraftet wird.

Mit jeder zusätzlichen Punktsteigerung pro Spiel stiegen die Chancen, dass ein Spieler gedraftet wird, um 1.319.