Korrelationsmatrix

In diesem Artikel erfahren Sie, was eine Korrelationsmatrix ist, wie ihre Formel lautet und wie eine Korrelationsmatrix zu interpretieren ist. Darüber hinaus können Sie sich ein konkretes Beispiel für die Interpretation einer Korrelationsmatrix ansehen.

Was ist eine Korrelationsmatrix?

Die Korrelationsmatrix ist eine Matrix, die an der Stelle i,j den Korrelationskoeffizienten zwischen den Variablen i und j enthält.

Daher ist die Korrelationsmatrix eine quadratische Matrix, die auf der Hauptdiagonale mit Einsen gefüllt ist, und das Element der Zeile i und der Spalte j besteht aus dem Wert des Korrelationskoeffizienten zwischen der Variablen i und der Variablen j .

Die Formel für die Korrelationsmatrix lautet daher wie folgt:

Gold

ist der Korrelationskoeffizient zwischen den Variablen

Und

Um die Korrelationsmatrix eines Datensatzes zu finden, ist es daher wichtig zu wissen, wie der Korrelationskoeffizient berechnet wird. Falls Sie sich nicht erinnern, erfahren Sie unter folgendem Link, wie es mit einem Online-Rechner geht:

Eine Eigenschaft des Korrelationskoeffizienten besteht darin, dass die Reihenfolge der Variablen für seine Berechnung, also den Korrelationskoeffizienten, keine Rolle spielt

ist äquivalent zu

Daher ist die Korrelationsmatrix symmetrisch.

Damit eine Korrelationsmatrix aussagekräftig ist, muss der statistische Datensatz mehr als zwei Variablen enthalten. Andernfalls würde die Bestimmung eines einzelnen Korrelationskoeffizienten genügen und die Korrelationsmatrix wäre aussagekräftig.

So erstellen Sie eine Korrelationsmatrix

Sehen wir uns anhand der Definition der Korrelationsmatrix an, wie diese Art von statistischer Matrix erstellt wird:

1. Berechnen Sie den Korrelationskoeffizienten jedes Variablenpaares. Beachten Sie, dass die Reihenfolge der Variablen das Ergebnis nicht verändert, sodass es nur einmal für jedes Variablenpaar berechnet werden muss.
2. Erstellen Sie eine quadratische Matrix mit der gleichen Dimension wie die Anzahl der Variablen in der Datenreihe. Diese Matrix wird die Korrelationsmatrix sein.
3. Tragen Sie in jedes Element der Hauptdiagonale der Korrelationsmatrix eine 1 ein.
4. Setzen Sie den Korrelationskoeffizienten der Variablen i , j an die Positionen i , j und j , i .
5. Nachdem die Korrelationsmatrix erstellt wurde, müssen nur noch deren Werte interpretiert werden.

Bedenken Sie, dass es nicht ausreicht, einfach nur die Korrelationsmatrix auszuführen. Anschließend müssen Sie deren Werte interpretieren und verstehen, was sie bedeuten. Im folgenden Abschnitt wird erläutert, wie eine Korrelationsmatrix interpretiert wird.

Interpretation der Korrelationsmatrix

Um die Korrelationsmatrix richtig zu interpretieren, muss berücksichtigt werden, dass der Wert des Korrelationskoeffizienten zwischen -1 und +1 liegen kann:

• r=-1 : Die beiden Variablen weisen eine perfekte negative Korrelation auf, sodass wir eine Linie mit negativer Steigung zeichnen können, in der alle Punkte miteinander verbunden sind.
• -1<r<0 : Die Korrelation zwischen den beiden Variablen ist negativ. Wenn also eine Variable zunimmt, nimmt die andere ab. Je näher der Wert bei -1 liegt, desto negativer sind die Variablen miteinander verknüpft.
• r=0 : Die Korrelation zwischen den beiden Variablen ist sehr schwach, tatsächlich ist die lineare Beziehung zwischen ihnen Null. Dies bedeutet nicht, dass die Variablen unabhängig sind, da sie möglicherweise in einem nichtlinearen Zusammenhang stehen.
• 0<r<1 : Die Korrelation zwischen den beiden Variablen ist positiv. Je näher der Wert an +1 liegt, desto stärker ist die Beziehung zwischen den Variablen. In diesem Fall tendiert eine Variable dazu, ihren Wert zu erhöhen, wenn auch die andere zunimmt.
• r=1 : Die beiden Variablen haben eine perfekte positive Korrelation, das heißt, sie haben eine positive lineare Beziehung.

Um die Korrelationsmatrix zu interpretieren, ist es daher notwendig, jeden Korrelationskoeffizienten zu interpretieren und die verschiedenen Ergebnisse zu vergleichen.

Auf diese Weise können Sie sehen, welche Variablen am stärksten miteinander verbunden sind, welche Variablen am wichtigsten sind, welche Variablen praktisch keine Beziehung zueinander haben usw.

Beispiel einer Korrelationsmatrix

Um vollständig zu verstehen, woraus die Korrelationsmatrix besteht und wie sie interpretiert wird, analysieren wir in diesem Abschnitt ein Beispiel einer Korrelationsmatrix:

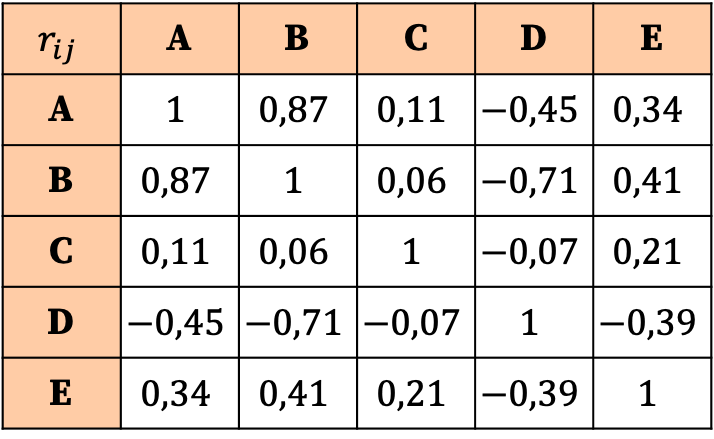
Die Interpretation der Korrelationsmatrix basiert auf den Werten der Koeffizienten. Somit können wir sehen, dass die stärkste Korrelation die Beziehung zwischen Variable A und Variable B ist, da ihr entsprechender Koeffizient am größten ist (0,87).

Andererseits hat die Variable C praktisch keine Korrelation mit irgendeiner Variablen, da alle ihre Koeffizienten sehr nahe bei Null liegen und daher sehr niedrig sind. Um die Analyse zu vereinfachen, könnten wir daher sogar in Betracht ziehen, diese Variable aus der statistischen Studie zu entfernen.

Ebenso sind alle Beziehungen der Variablen D zu anderen Variablen negativ, was bedeutet, dass die Korrelation zwischen der Variablen D und anderen Variablen umgekehrt ist. Dies bedeutet nicht, dass die Variable eliminiert werden sollte, sondern lediglich, dass die Variable D negativ korreliert ist.

Wie Sie sehen, ist die Korrelationsmatrix sehr nützlich, um die Daten zusammenzufassen und eine Gesamtanalyse der Beziehung zwischen verschiedenen Variablen im Datensatz durchzuführen.