So erstellen sie ein qq-diagramm in python

Ein QQ-Plot , kurz für „Quantil-Quantil“, wird häufig verwendet, um zu bewerten, ob ein Datensatz möglicherweise aus einer theoretischen Verteilung stammt oder nicht.

In den meisten Fällen wird dieser Diagrammtyp verwendet, um zu bestimmen, ob ein Datensatz einer Normalverteilung folgt oder nicht.

In diesem Tutorial wird erläutert, wie Sie in Python ein QQ-Diagramm für einen Datensatz erstellen.

Beispiel: QQ-Plot in Python

Angenommen, wir haben den folgenden Datensatz mit 100 Werten:

 import numpy as np

#create dataset with 100 values that follows a normal distribution
np.random.seed(0)
data = np.random.normal(0,1, 1000)

#view first 10 values
data[:10] 

array([ 1.76405235, 0.40015721, 0.97873798, 2.2408932 , 1.86755799,
       -0.97727788, 0.95008842, -0.15135721, -0.10321885, 0.4105985 ])

Um ein QQ-Diagramm für diesen Datensatz zu erstellen, können wir die Funktion qqplot() aus der Statsmodels-Bibliothek verwenden:

 import statsmodels.api as sm
import matplotlib.pyplot as plt

#create QQ plot with 45-degree line added to plot
fig = sm.qqplot(data, line='45')
plt.show()

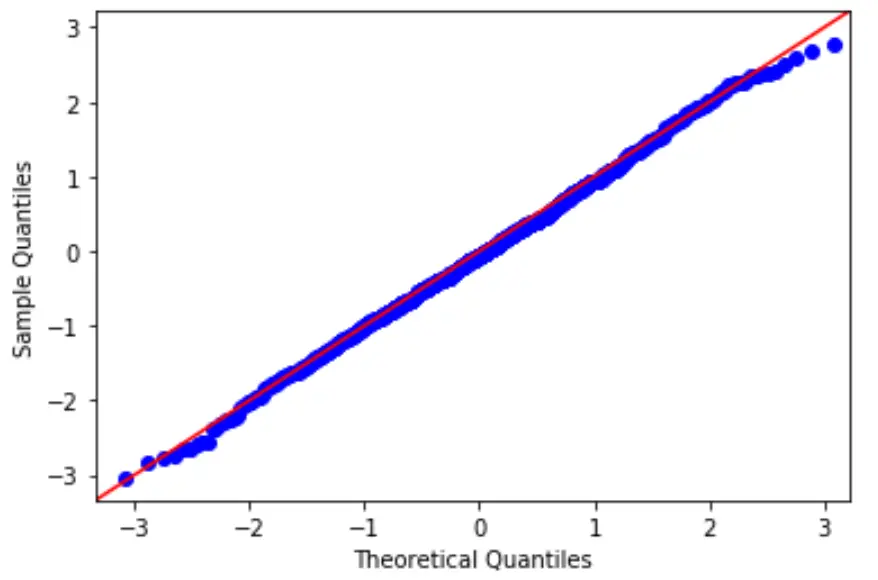
In einem QQ-Diagramm zeigt die x-Achse die theoretischen Quantile an. Das bedeutet, dass nicht Ihre tatsächlichen Daten angezeigt werden, sondern vielmehr, wo sich Ihre Daten befinden würden, wenn sie normalverteilt wären.

Die Y-Achse zeigt Ihre aktuellen Daten an. Das bedeutet, dass die Daten normalverteilt sind, wenn die Datenwerte einer annähernd geraden Linie im 45-Grad-Winkel folgen.

In unserem obigen QQ-Diagramm können wir sehen, dass die Datenwerte dazu neigen, eng an den 45-Grad-Winkel zu halten, was bedeutet, dass die Daten wahrscheinlich normalverteilt sind. Dies sollte nicht überraschen, da wir die 100 Datenwerte mit der Funktion numpy.random.normal() generiert haben.

Überlegen Sie stattdessen, ob wir einen Datensatz mit 100 gleichmäßig verteilten Werten generieren und ein QQ-Diagramm für diesen Datensatz erstellen würden:

 #create dataset of 100 uniformly distributed values
data = np.random.uniform(0,1, 1000)

#generate QQ plot for the dataset
fig = sm.qqplot(data, line='45')
plt.show()

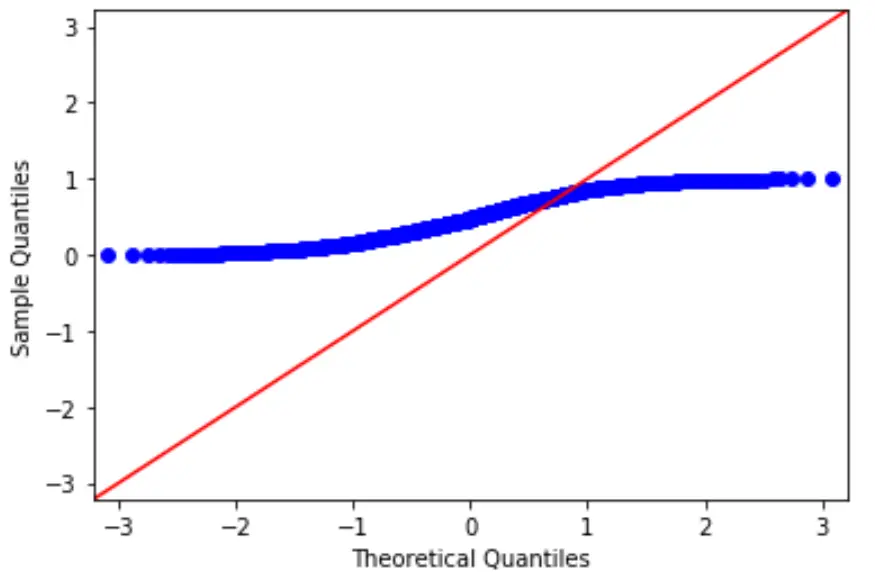
Die Datenwerte folgen eindeutig nicht der roten 45-Grad-Linie, was darauf hindeutet, dass sie keiner Normalverteilung folgen.

Hinweise zu QQ-Plots

Beachten Sie die folgenden Hinweise zu QQ-Diagrammen:

• Obwohl es sich bei einem QQ-Diagramm nicht um einen formalen statistischen Test handelt, bietet er eine einfache Möglichkeit, visuell zu überprüfen, ob ein Datensatz normalverteilt ist oder nicht.
• Achten Sie darauf, QQ-Plots nicht mit PP-Plots zu verwechseln, die seltener verwendet werden und weniger nützlich für die Analyse von Datenwerten sind, die am Ende der Verteilung liegen.

Weitere Python-Tutorials finden Sie hier .