So erstellen sie ein restdiagramm in python

Ein Residuendiagramm ist eine Art Diagramm, das angepasste Werte gegenüber den Residuen eines Regressionsmodells anzeigt.

Diese Art von Diagramm wird häufig verwendet, um zu bewerten, ob ein lineares Regressionsmodell für einen bestimmten Datensatz geeignet ist oder nicht, und um Residuen auf Heteroskedastizität zu prüfen.

In diesem Tutorial wird erläutert, wie Sie in Python ein Residuendiagramm für ein lineares Regressionsmodell erstellen.

Beispiel: Residuenplot in Python

Für dieses Beispiel verwenden wir einen Datensatz, der die Attribute von 10 Basketballspielern beschreibt:

 import numpy as np
import pandas as pd

#create dataset
df = pd.DataFrame({'rating': [90, 85, 82, 88, 94, 90, 76, 75, 87, 86],
                   'points': [25, 20, 14, 16, 27, 20, 12, 15, 14, 19],
                   'assists': [5, 7, 7, 8, 5, 7, 6, 9, 9, 5],
                   'rebounds': [11, 8, 10, 6, 6, 9, 6, 10, 10, 7]})

#view dataset
df

	rating points assists rebounds
0 90 25 5 11
1 85 20 7 8
2 82 14 7 10
3 88 16 8 6
4 94 27 5 6
5 90 20 7 9
6 76 12 6 6
7 75 15 9 10
8 87 14 9 10
9 86 19 5 7

Residuendiagramm für einfache lineare Regression

Angenommen, wir passen ein einfaches lineares Regressionsmodell an und verwenden dabei Punkte als Prädiktorvariable und Note als Antwortvariable:

 #import necessary libraries
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.formula.api import ols

#fit simple linear regression model
model = ols('rating ~ points', data=df). fit ()

#view model summary
print(model.summary())

Mit der Funktion plot_regress_exog() aus der Statsmodels-Bibliothek können wir ein Residuen- oder angepasstes Diagramm erstellen:

 #define figure size
fig = plt.figure(figsize=(12,8))

#produce regression plots
fig = sm.graphics.plot_regress_exog(model, ' points ', fig=fig)

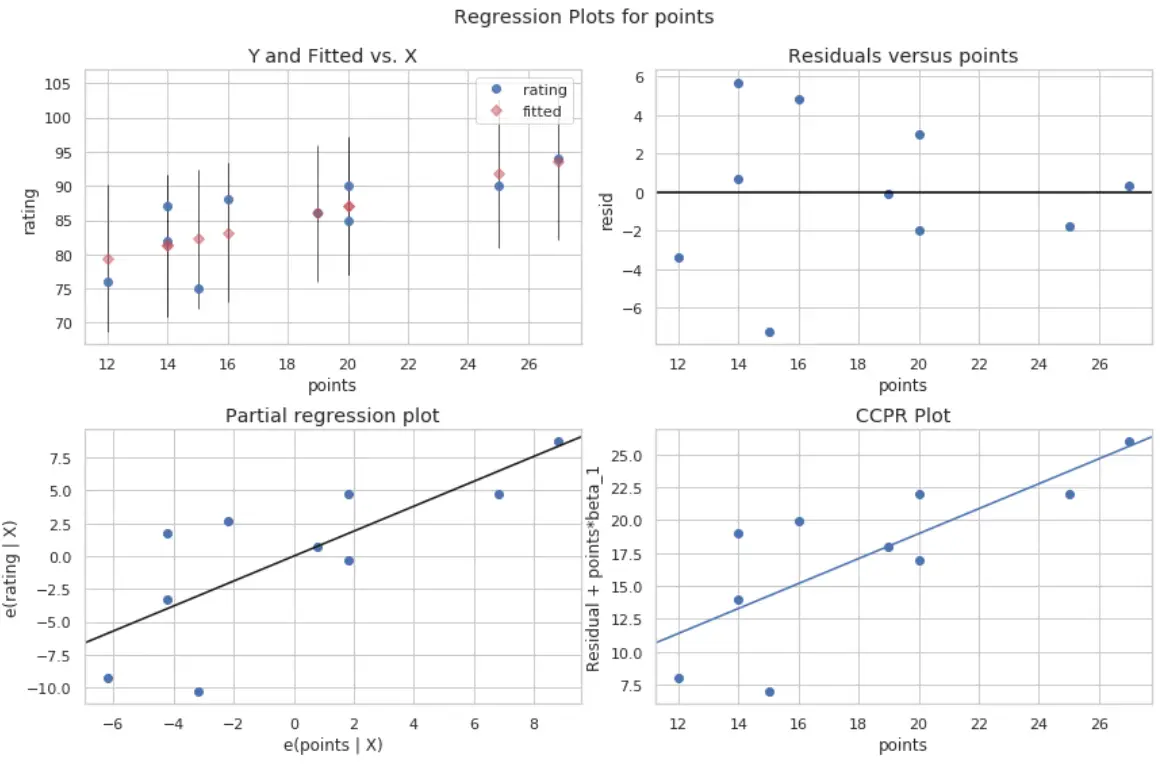
Es entstehen vier Parzellen. Das Bild in der oberen rechten Ecke ist das Residualdiagramm im Vergleich zum angepassten Diagramm. Die x-Achse in diesem Diagramm zeigt die tatsächlichen Werte der Prädiktorvariablenpunkte und die y-Achse zeigt das Residuum für diesen Wert.

Da die Residuen zufällig um Null herum verstreut zu sein scheinen, deutet dies darauf hin, dass Heteroskedastizität bei der Prädiktorvariablen kein Problem darstellt.

Residuendiagramme für multiple lineare Regression

Angenommen, wir passen stattdessen ein multiples lineares Regressionsmodell an, das Assists und Rebounds als Prädiktorvariable und die Bewertung als Antwortvariable verwendet:

 #fit multiple linear regression model
model = ols('rating ~ assists + rebounds', data=df). fit ()

#view model summary
print(model.summary())

Auch hier können wir mit der Funktion plot_regress_exog() aus der Statsmodels-Bibliothek ein Residuum-gegen-Prädiktor-Diagramm für jeden einzelnen Prädiktor erstellen.

So sieht beispielsweise das Residuen-/Prädiktordiagramm für Prädiktorvariablenunterstützungen aus:

 #create residual vs. predictor plot for 'assists'
fig = plt.figure(figsize=(12,8))
fig = sm.graphics.plot_regress_exog(model, ' assists ', fig=fig)

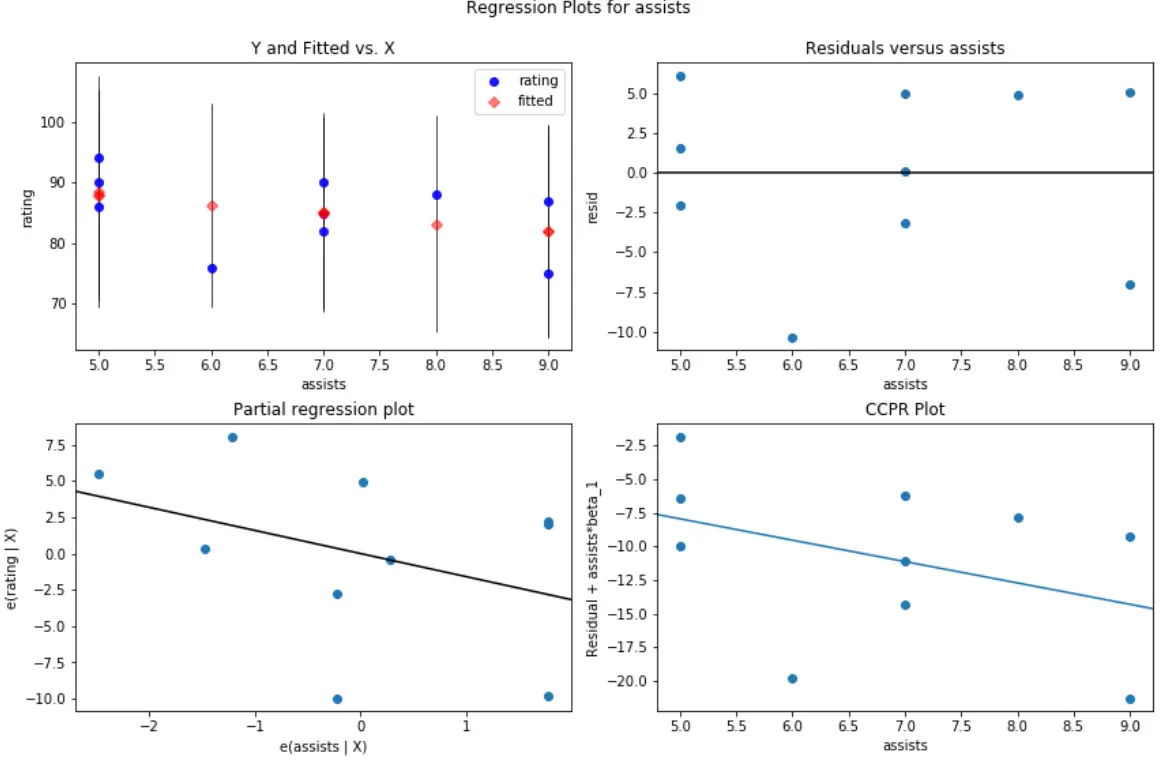
Und so sieht das Residuen-/Prädiktordiagramm für die Prädiktorvariablen- Bounces aus:

 #create residual vs. predictor plot for 'assists'
fig = plt.figure(figsize=(12,8))
fig = sm.graphics.plot_regress_exog(model, ' rebounds ', fig=fig)

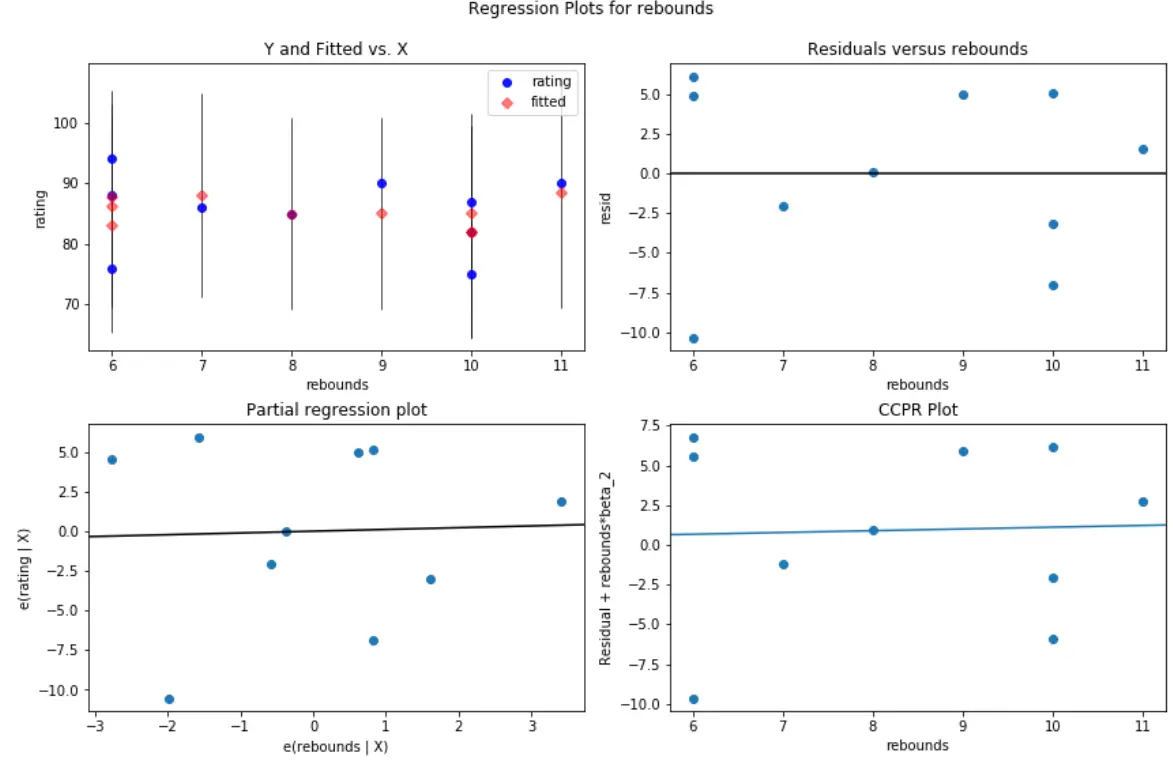
In beiden Diagrammen scheinen die Residuen zufällig um Null herum gestreut zu sein, was darauf hindeutet, dass Heteroskedastizität bei keiner der Prädiktorvariablen im Modell ein Problem darstellt.