Operationen auf mengen: vereinigung, schnittmenge, komplement und differenz

Eine Menge ist eine Sammlung von Elementen.

Wir bezeichnen eine Menge mit einem Großbuchstaben und definieren die Elemente der Menge mit geschweiften Klammern. Angenommen, wir haben eine Menge namens „A“ mit den Elementen 1, 2, 3. Wir würden dies wie folgt schreiben:

A = {1, 2, 3}

In diesem Tutorial werden die am häufigsten verwendeten Mengenoperationen in der Wahrscheinlichkeitsrechnung und Statistik erläutert.

Union

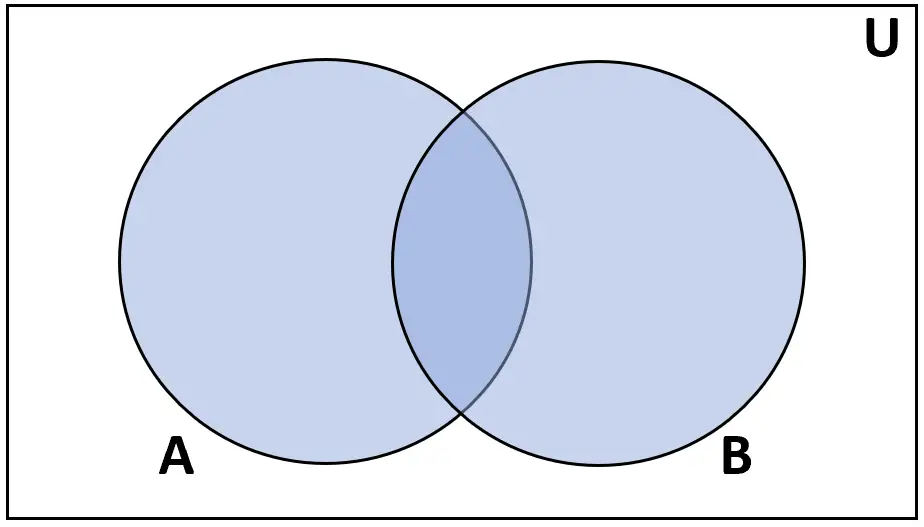
Definition: Die Vereinigung der Mengen A und B ist die Menge der Elemente, die entweder in A oder in B vorkommen.

Bewertung: A ∪ B

Beispiele:

• {1, 2, 3} ∪ {4, 5, 6} = {1, 2, 3, 4, 5, 6}
• {1, 2} ∪ {1, 2} = {1, 2}
• {1, 2, 3} ∪ {3, 4} = {1, 2, 3, 4}

Überschneidung

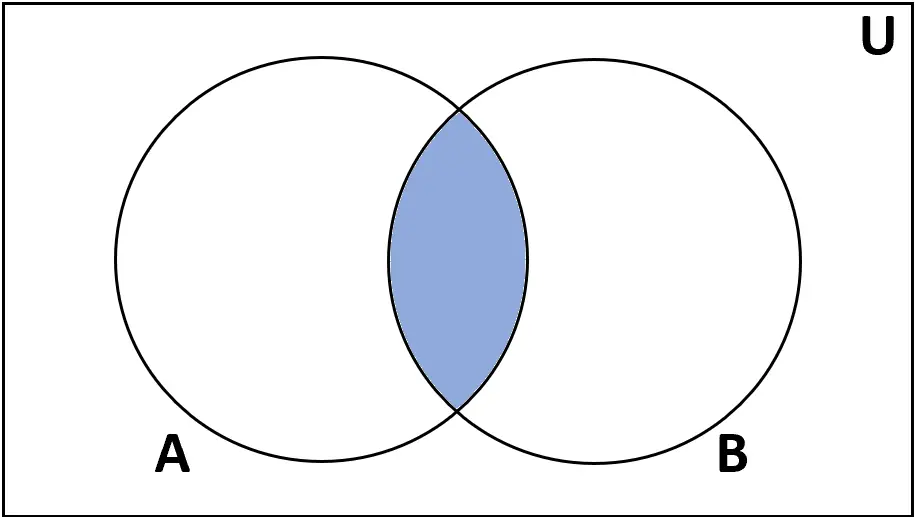
Definition: Der Schnittpunkt der Mengen A und B ist die Menge der Elemente, die sowohl in A als auch in B vorkommen.

Notation: A ∩ B

Beispiele:

• {1, 2, 3} ∩ {4, 5, 6} = {∅}
• {1, 2} ∩ {1, 2} = {1, 2}
• {1, 2, 3} ∩ {3, 4} = {3}

Ergänzen

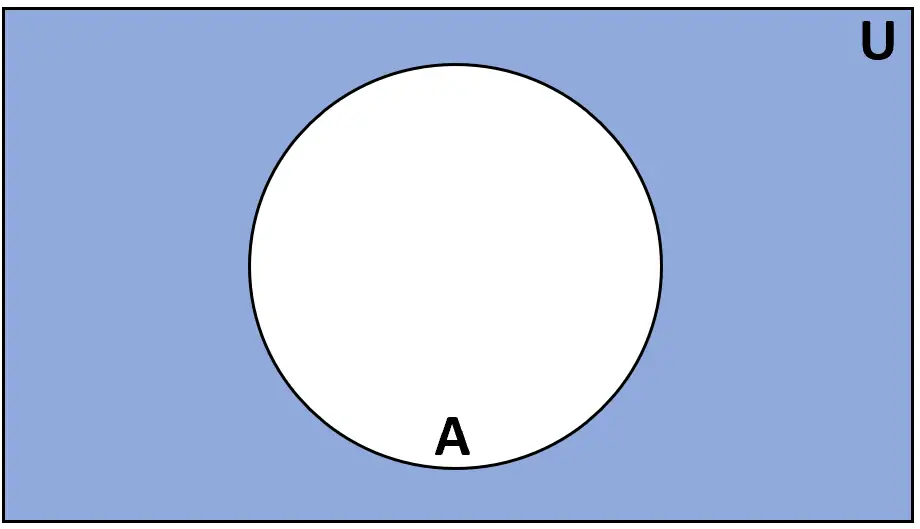
Definition: Das Komplement der Menge A ist die Menge der Elemente, die in der Universalmenge U, aber nicht in A enthalten sind.

Bewertung: A‘ oder ^Ac

Beispiele:

• Wenn U = {1, 2, 3, 4, 5, 6} und A = {1, 2}, dann A ^c = {3, 4, 5, 6}
• Wenn U = {1, 2, 3} und A = {1, 2}, dann A ^c = {3}

Unterschied

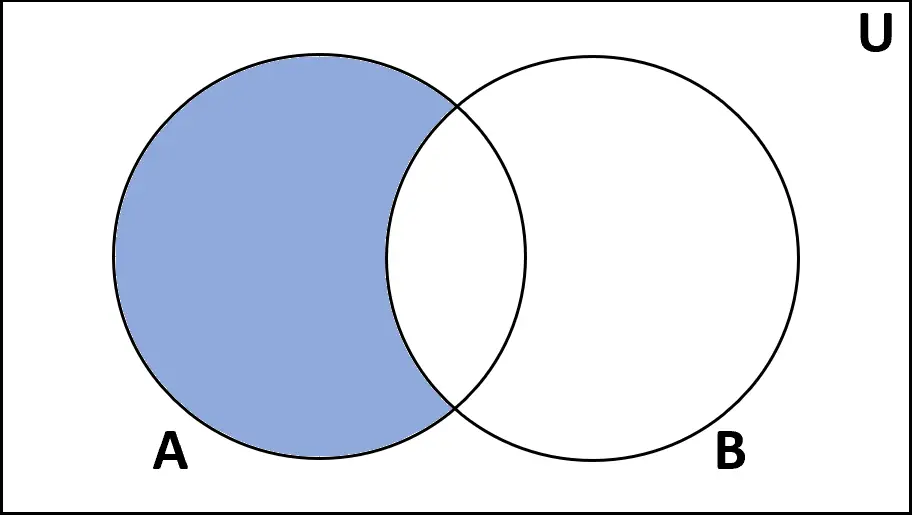
Definition: Der Unterschied zwischen den Mengen A und B ist die Menge der Elemente, die in A, aber nicht in B vorkommen.

Bewertungen: A–B

Beispiele:

• {1, 2, 3} – {2, 3, 4} = {1}
• {1, 2} – {1, 2} = {∅}
• {1, 2, 3} – {4, 5} = {1, 2, 3}

Symmetrischer Unterschied

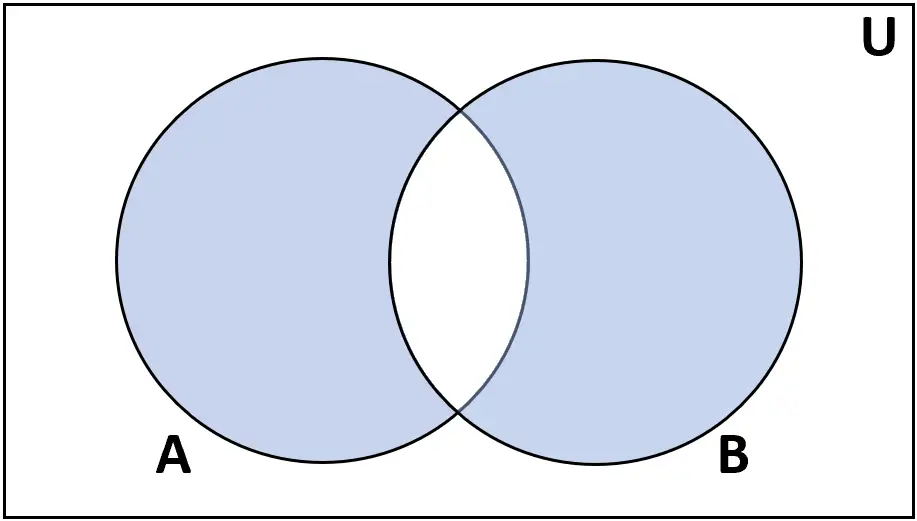
Definition: Die symmetrische Differenz der Mengen A und B ist die Menge der Elemente, die entweder in A oder B, aber nicht in beiden vorkommen.

Bewertung: AΔB

Beispiele:

• {1, 2, 3} Δ {2, 3, 4} = {1, 4}
• {1, 2} Δ {1, 2} = {∅}
• {1, 2, 3} Δ {4, 5} = {1, 2, 3, 4, 5}

kartesisches Produkt

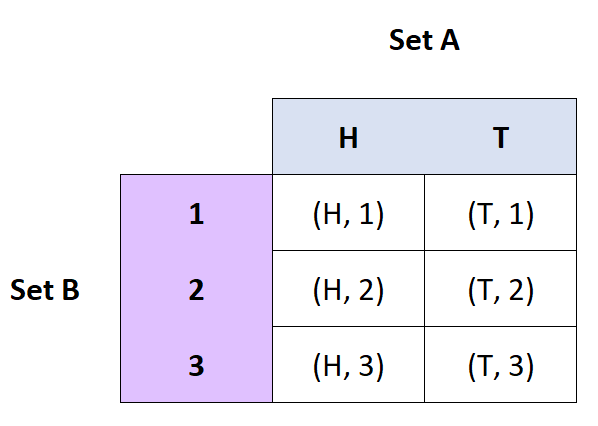
Definition: Das kartesische Produkt der Mengen A und B ist die Menge der geordneten Paare von A und B.

Bewertung: A x B

Beispiele:

• Wenn A = {H, T} und B = {1, 2, 3}, dann ist A x B = {(H, 1), (H, 2), (H, 3), (T, 1), ( T, 2), (T, 3)}
• Wenn A = {T, H} und B = {1, 2, 3}, dann ist A x B = {(T, 1), (T, 2), (T, 3), (H, 1), ( H, 2), (H, 3)}