So berechnen sie den standardfehler des mittelwerts in excel

Der Standardfehler des Mittelwerts ist eine Möglichkeit, die Verteilung von Werten in einem Datensatz zu messen. Es wird wie folgt berechnet:

Standardfehler = s / √n

Gold:

• s : Stichprobenstandardabweichung
• n : Stichprobengröße

Sie können den Standardfehler des Mittelwerts eines beliebigen Datensatzes in Excel mithilfe der folgenden Formel berechnen:

= STDEV (Wertebereich) / SQRT ( COUNT (Wertebereich))

Das folgende Beispiel zeigt, wie diese Formel verwendet wird.

Beispiel: Standardfehler in Excel

Angenommen, wir haben den folgenden Datensatz:

Der folgende Screenshot zeigt, wie der Standardfehler des Mittelwerts für diesen Datensatz berechnet wird:

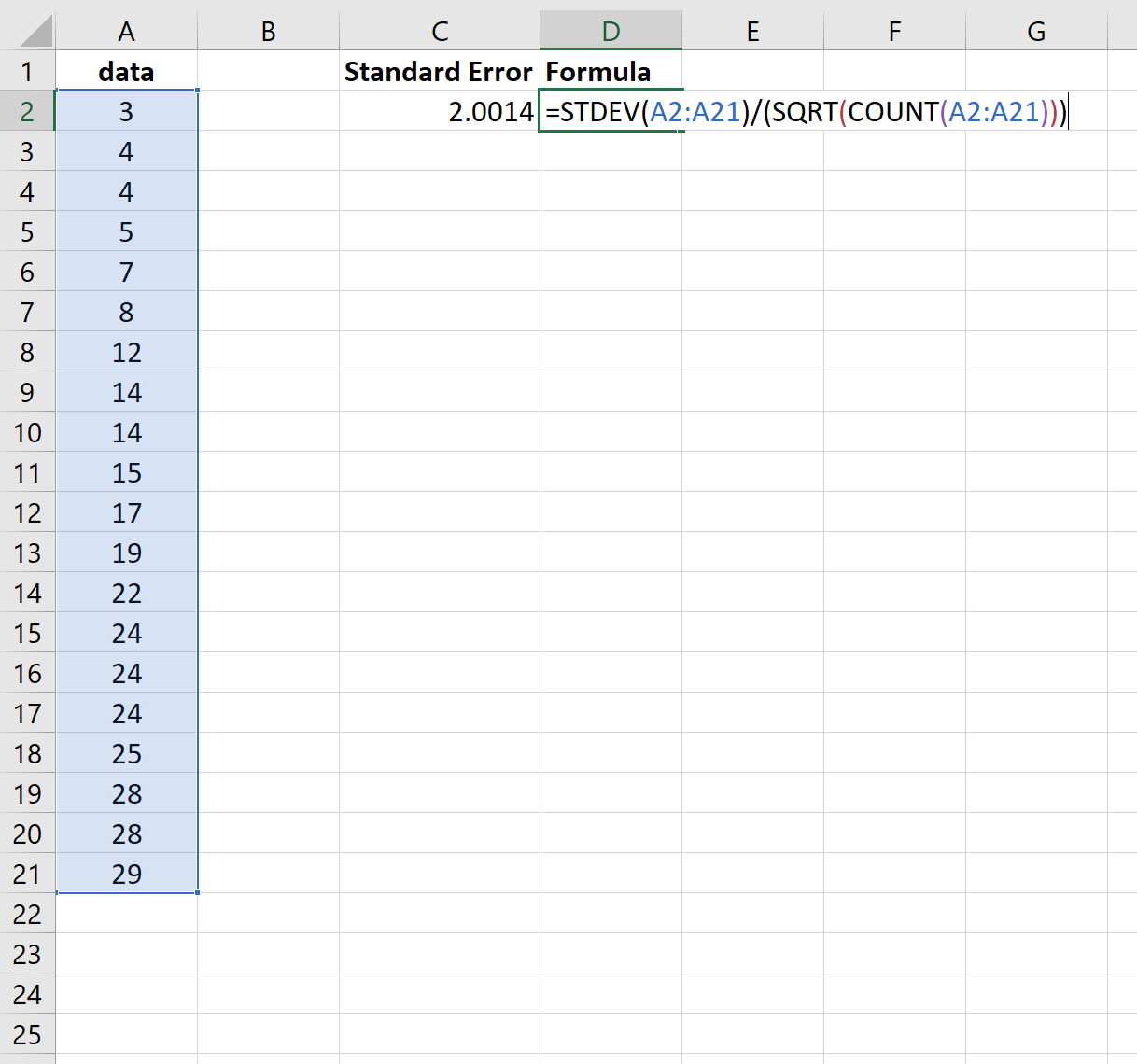
Der Standardfehler beträgt 2,0014 .

Beachten Sie, dass die Funktion =STDEV() den Stichprobenmittelwert berechnet, was der Funktion =STDEV.S() in Excel entspricht.

Wir hätten also die folgende Formel verwenden können, um die gleichen Ergebnisse zu erzielen:

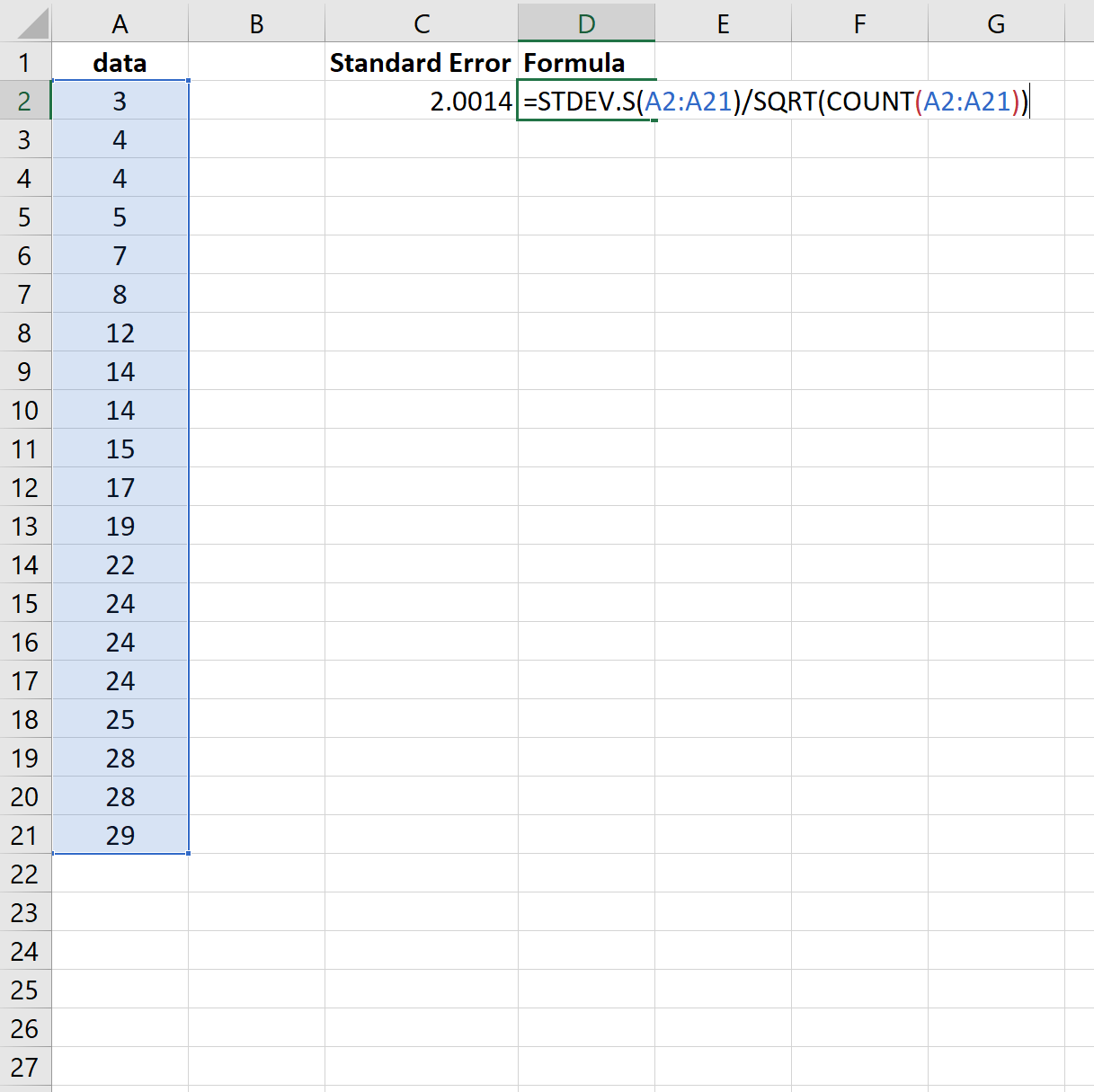
Auch hier stellt sich heraus, dass der Standardfehler 2,0014 beträgt.

So interpretieren Sie den Standardfehler des Mittelwerts

Der Standardfehler des Mittelwerts ist einfach ein Maß für die Streuung der Werte um den Mittelwert. Bei der Interpretation des Standardfehlers des Mittelwerts sind zwei Dinge zu beachten:

1. Je größer der Standardfehler des Mittelwerts ist, desto stärker streuen die Werte in einem Datensatz um den Mittelwert.

Um dies zu veranschaulichen, stellen wir uns vor, wir würden den letzten Wert des vorherigen Datensatzes um eine viel größere Zahl ändern:

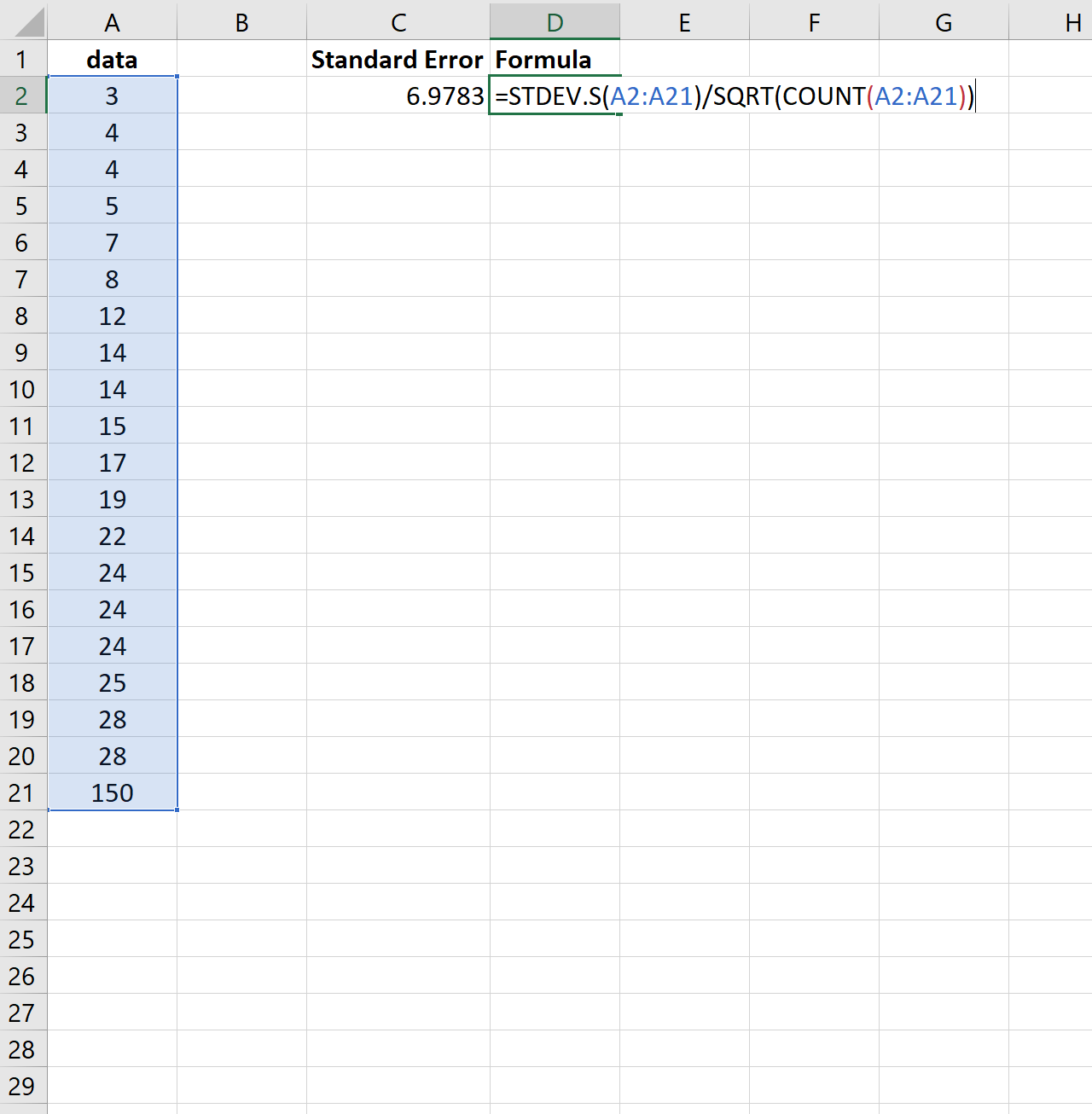
Beachten Sie, wie der Standardfehler von 2,0014 auf 6,9783 ansteigt. Dies weist darauf hin, dass die Werte in diesem Datensatz im Vergleich zum vorherigen Datensatz stärker um den Mittelwert verteilt sind.

2. Mit zunehmender Stichprobengröße nimmt der Standardfehler des Mittelwerts tendenziell ab.

Um dies zu veranschaulichen, betrachten Sie den Standardfehler des Mittelwerts für die folgenden zwei Datensätze:

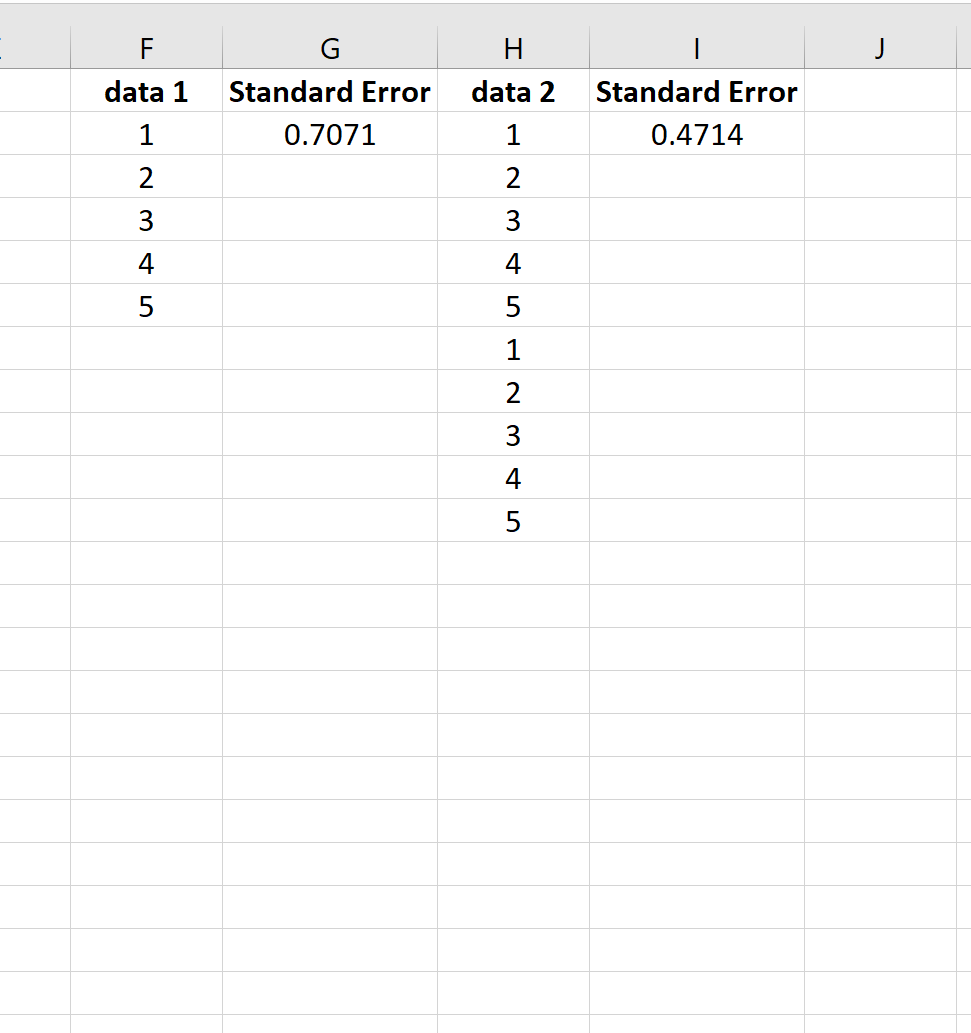
Der zweite Datensatz ist einfach der erste Datensatz, der zweimal wiederholt wird. Beide Datensätze haben also den gleichen Mittelwert, aber der zweite Datensatz hat eine größere Stichprobengröße und daher einen kleineren Standardfehler.