Kumulierte absolute häufigkeit
In diesem Artikel wird erklärt, was die akkumulierte absolute Frequenz ist und wofür sie verwendet wird. Sie finden also die Definition der kumulativen absoluten Häufigkeit, wie man die kumulative absolute Häufigkeit aus einem Datensatz ermittelt und außerdem zwei Übungen, die Schritt für Schritt gelöst werden.
Was ist die kumulative absolute Häufigkeit?
In der Statistik ist die kumulative absolute Häufigkeit die kumulative Summe der absoluten Häufigkeiten. Das heißt, die kumulative absolute Häufigkeit eines Werts ist gleich der absoluten Häufigkeit dieses Werts plus der absoluten Häufigkeit aller Werte, die kleiner als dieser sind.
Normalerweise wird in der Statistik der Großbuchstabe F mit dem tiefgestellten Index i verwendet, um die kumulative absolute Häufigkeit des Werts i darzustellen, daher ist das Symbol für die kumulative absolute Häufigkeit F i .
Um zu verstehen, was die akkumulierte absolute Häufigkeit bedeutet, müssen Sie sich logischerweise über das Konzept der absoluten Häufigkeit im Klaren sein. Daher wird empfohlen, den folgenden Artikel zu lesen, bevor Sie mit der Erklärung fortfahren.
So berechnen Sie die kumulative absolute Häufigkeit
Die Schritte zur Berechnung der kumulativen absoluten Häufigkeit sind wie folgt:
- Erstellen Sie eine Tabelle mit allen unterschiedlichen Werten, die im Datensatz erscheinen, d. h. platzieren Sie jeden unterschiedlichen Wert in einer Zeile einer Tabelle.
- Bestimmt die absolute Häufigkeit jedes Werts.
- Ermitteln Sie die kumulative absolute Häufigkeit jedes Werts. Sie wird berechnet, indem Sie die absolute Häufigkeit des Werts selbst plus die absoluten Häufigkeiten aller kleineren Werte addieren.
Beachten Sie, dass Sie bei kontinuierlichen Variablen oder vielen verschiedenen Werten zunächst die Daten in Intervallen gruppieren und dann die oben erläuterten Schritte anwenden müssen, um die kumulative absolute Häufigkeit zu ermitteln.
Beispiele für kumulative absolute Häufigkeit
Damit Sie sehen können, wie die kumulative absolute Häufigkeit berechnet wird, finden Sie im Folgenden Schritt für Schritt zwei Beispiele aus der Praxis. Im ersten Beispiel wurden die kumulierten absoluten Häufigkeiten einer diskreten Variablen und im zweiten Schritt einer kontinuierlichen Variablen berechnet.
Beispiel 1: diskrete Variable
- Die in der Statistik in einer Klasse mit 30 Schülern erzielten Noten lauten wie folgt. Wie groß ist die kumulative absolute Häufigkeit jeder Note?
![]()
![]()
![]()
Da alle Zahlen nur ganze Zahlen sein können, handelt es sich um eine diskrete Variable. Eine Gruppierung der Daten in Intervalle ist daher nicht erforderlich.
Um die kumulative absolute Häufigkeit zu bestimmen, müssen wir also zunächst die absolute Häufigkeit jedes Werts ermitteln, also die Häufigkeit, mit der jeder Wert in der statistischen Stichprobe vorkommt.

Da wir nun die absolute Häufigkeit kennen, können wir die kumulative absolute Häufigkeit berechnen. Dazu haben wir zwei Möglichkeiten: Entweder wir addieren die absolute Häufigkeit des Wertes plus alle absoluten Häufigkeiten der kleinsten Werte, oder im Gegenteil, wir addieren die absolute Häufigkeit des Werts plus die kumulative absolute Häufigkeit der vorherigen Werte . Wert.

Kurz gesagt sieht die Tabelle mit der absoluten kumulativen Trainingshäufigkeit wie folgt aus:

Beachten Sie, dass die kumulierte absolute Häufigkeit des letzten Werts immer der Gesamtzahl der Daten entspricht. Andernfalls liegt ein Fehler bei der Berechnung vor.
Beispiel 2: kontinuierliche Variable
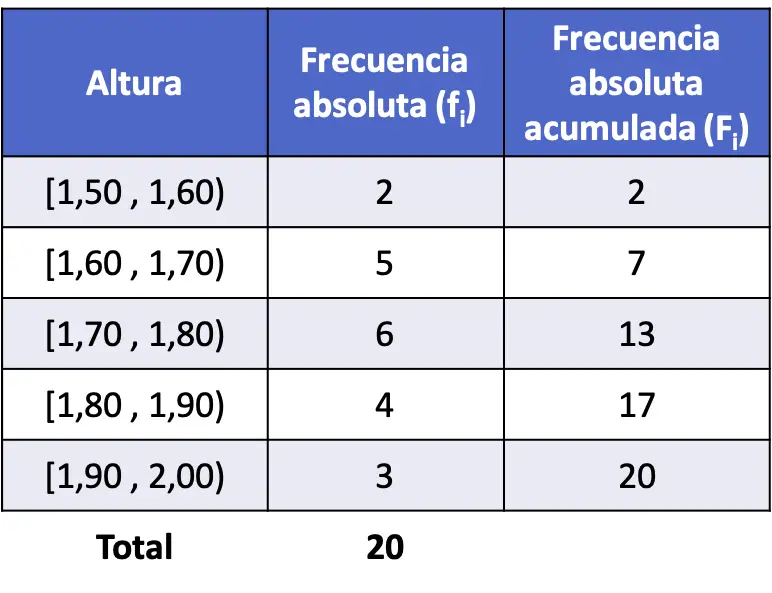
- Die Körpergröße von 20 Personen wurde gemessen und die unten gezeigten Ergebnisse erzielt. Zerlegt Daten in Intervalle und berechnet die kumulative absolute Häufigkeit für jedes Intervall.
![]()
![]()
Die Verteilung in diesem Beispiel ist kontinuierlich, da es Dezimalzahlen geben kann. Daher ist es am besten, die Daten in verschiedene Intervalle zu gruppieren.
Wir unterteilen die Daten also in Intervalle und zählen, wie oft eine Zahl in jedem Intervall vorkommt, um die absolute Häufigkeit zu erhalten:

Um dann die kumulative absolute Häufigkeit zu bestimmen, addieren Sie einfach die absoluten Häufigkeiten aller vorherigen Werte plus die absolute Häufigkeit des betreffenden Werts:
Kumulierte absolute Häufigkeit und kumulative relative Häufigkeit
Der Unterschied zwischen kumulativer absoluter Häufigkeit und kumulativer relativer Häufigkeit entspricht dem Typ der kumulativen Häufigkeit. Die akkumulierte absolute Häufigkeit ist gleich der Summe der absoluten Häufigkeiten der gleichen oder niedrigeren Werte, während die akkumulierte relative Häufigkeit den relativen Häufigkeiten der gleichen oder niedrigeren Werte entspricht.
Die kumulative absolute Häufigkeit wird also aus der absoluten Häufigkeit berechnet, während die kumulative relative Häufigkeit aus der relativen Häufigkeit berechnet wird.
Ein Beispiel für die Berechnung der kumulativen relativen Häufigkeit finden Sie hier: