Angepasstes quotenverhältnis: definition + beispiele

In der Statistik gibt uns ein Odds Ratio das Verhältnis zwischen der Wahrscheinlichkeit des Auftretens eines Ereignisses in einer Behandlungsgruppe und der Wahrscheinlichkeit des Auftretens eines Ereignisses in einer Kontrollgruppe an.

Quotenverhältnisse treten am häufigsten in der logistischen Regression auf. Hierbei handelt es sich um eine Methode, mit der wir ein Regressionsmodell anpassen, das über eine oder mehrere Prädiktorvariablen und eine binäre Antwortvariable verfügt.

Ein angepasstes Quotenverhältnis ist ein Quotenverhältnis, das für andere Prädiktorvariablen in einem Modell angepasst wurde.

Dies ist besonders nützlich, um zu verstehen, wie sich eine Prädiktorvariable auf die Wahrscheinlichkeit des Eintretens eines Ereignisses auswirkt, nachdem die Wirkung anderer Prädiktorvariablen berücksichtigt wurde.

Das folgende Beispiel veranschaulicht den Unterschied zwischen einem Quotenverhältnis und einem angepassten Quotenverhältnis.

Beispiel: Berechnung angepasster Quotenverhältnisse

Angenommen, wir möchten verstehen, ob das Alter einer Mutter die Wahrscheinlichkeit beeinflusst, ein Baby mit niedrigem Geburtsgewicht zu bekommen.

Um dies zu untersuchen, können wir eine logistische Regression durchführen, wobei wir das Alter als Prädiktorvariable und ein niedriges Geburtsgewicht (ja oder nein) als Antwortvariable verwenden.

Angenommen, wir sammeln Daten von 300 Müttern und passen ein logistisches Regressionsmodell an. Hier sind die Ergebnisse:

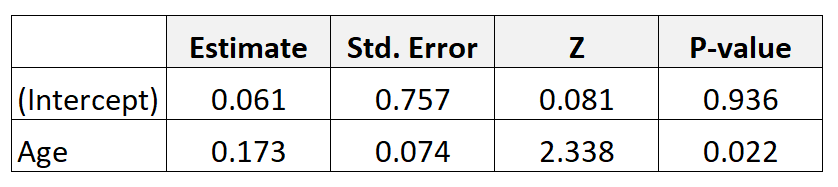
Um das Quotenverhältnis für das Alter zu erhalten, potenzieren Sie einfach die Koeffizientenschätzung aus der Tabelle: e ^0,173 = 1,189 .

Dies zeigt uns, dass ein Anstieg des Alters um ein Jahr mit einer um 1.189 höheren Wahrscheinlichkeit verbunden ist, dass ein Baby ein niedriges Geburtsgewicht hat. Mit anderen Worten: Die Wahrscheinlichkeit, ein Kind mit niedrigem Geburtsgewicht zu bekommen, steigt mit jedem weiteren jährlichen Altersanstieg um 18,9 % .

Dieses Quotenverhältnis wird als „rohes“ Quotenverhältnis oder „nicht angepasstes“ Quotenverhältnis bezeichnet, da es nicht für die anderen Prädiktorvariablen im Modell angepasst wurde, da es die einzige Prädiktorvariable im Modell ist.

Aber nehmen wir an, wir wollen verstehen, ob das Alter und die Rauchgewohnheiten einer Mutter die Wahrscheinlichkeit beeinflussen, ein Baby mit niedrigem Geburtsgewicht zu bekommen.

Um dies zu untersuchen, können wir eine logistische Regression durchführen, indem wir Alter und Rauchen (ja oder nein) als Prädiktorvariablen und niedriges Geburtsgewicht als Antwortvariable verwenden.

Angenommen, wir sammeln Daten von 300 Müttern und passen ein logistisches Regressionsmodell an. Hier sind die Ergebnisse:

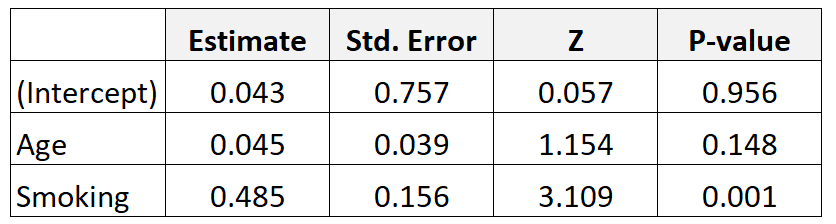
So interpretieren Sie die Ergebnisse:

Alter: Das altersbereinigte Odds Ratio wird wie folgt berechnet: e ^0,045 = 1,046 . Dies bedeutet, dass die Wahrscheinlichkeit, ein Kind mit niedrigem Geburtsgewicht zu bekommen, mit jedem weiteren jährlichen Altersanstieg um 4,6 % steigt, vorausgesetzt, die Rauchervariable bleibt konstant.

Angenommen, Mutter A und Mutter B rauchen beide. Wenn Mutter A ein Jahr älter als Mutter B ist, beträgt die Wahrscheinlichkeit, dass Mutter A ein Kind mit niedrigem Geburtsgewicht bekommt, das 1,046-fache der Wahrscheinlichkeit, dass Mutter B ein Kind mit niedrigem Geburtsgewicht bekommt.

Rauchen : Das angepasste Odds Ratio für Rauchen wird wie folgt berechnet: ^e.485 = 1.624 . Dies bedeutet, dass die Wahrscheinlichkeit, ein Kind mit niedrigem Geburtsgewicht zu bekommen, um 62,4 % steigt, wenn die Mutter raucht (im Vergleich zur Nichtraucherin), vorausgesetzt, die Altersvariable bleibt konstant.

Angenommen, Mutter A und Mutter B sind beide 30 Jahre alt. Wenn Mutter A während der Schwangerschaft raucht und Mutter B nicht raucht, ist die Wahrscheinlichkeit, dass Mutter A ein Kind mit niedrigem Geburtsgewicht bekommt, um 62,4 % höher als die Wahrscheinlichkeit, dass Mutter B ein Kind mit niedrigem Geburtsgewicht bekommt.

Beachten Sie, dass das altersbereinigte Quotenverhältnis niedriger ist als das nicht angepasste Quotenverhältnis aus dem vorherigen Beispiel. Dies liegt daran, dass, wenn andere Prädiktorvariablen die Wahrscheinlichkeit erhöhen, dass die Antwortvariable auftritt, das angepasste Quotenverhältnis für eine bereits im Modell vorhandene Prädiktorvariable immer sinkt.

Zusammenfassung: Quotenverhältnis im Vergleich zum angepassten Quotenverhältnis

Ein Quotenverhältnis (manchmal auch „rohes“ Quotenverhältnis genannt) ist nützlich, um uns zu sagen, wie sich Änderungen einer Prädiktorvariablen auf die Wahrscheinlichkeit des Auftretens einer Antwortvariablen auswirken.

Ein angepasstes Quotenverhältnis ist nützlich, um uns zu sagen, wie sich Änderungen einer Prädiktorvariablen auf die Wahrscheinlichkeit des Auftretens einer Antwortvariablen auswirken, nachdem andere Prädiktorvariablen in einem Modell berücksichtigt wurden.

Zusätzliche Ressourcen

Einführung in die logistische Regression
So führen Sie eine logistische Regression in R durch
So führen Sie eine logistische Regression in Python durch