Die hypothese der konstanten varianz: definition und beispiel

Die lineare Regression ist eine Technik, mit der wir die Beziehung zwischen einer oder mehreren Prädiktorvariablen und einer Antwortvariablen quantifizieren.

Eine der wichtigsten Annahmen der linearen Regression besteht darin, dass die Residuen auf jeder Ebene der Prädiktorvariablen eine konstante Varianz aufweisen.

Wenn diese Annahme nicht bestätigt wird, würden die Residuen unter Heteroskedastizität leiden. Wenn dies geschieht, werden die Schätzungen der Modellkoeffizienten unzuverlässig.

So bewerten Sie die konstante Varianz

Die gebräuchlichste Methode zur Bestimmung, ob die Residuen eines Regressionsmodells eine konstante Varianz aufweisen, besteht darin, ein Diagramm der angepassten Werte gegen die Residuen zu erstellen.

Dies ist eine Art Diagramm, das die angepassten Werte des Regressionsmodells entlang der x-Achse und die Residuen dieser angepassten Werte entlang der y-Achse anzeigt.

Wenn die Verteilung der Residuen auf jeder Ebene der angepassten Werte ungefähr gleich ist, sagen wir, dass die Annahme einer konstanten Varianz erfüllt ist.

Andernfalls wird diese Annahme wahrscheinlich verletzt, wenn die Streuung der Residuen systematisch zunimmt oder abnimmt.

Hinweis : Diese Art von Diagramm kann nur erstellt werden , nachdem ein Regressionsmodell an den Datensatz angepasst wurde.

Das folgende Diagramm zeigt ein Beispiel für ein Diagramm angepasster Werte gegenüber Residuen, das eine konstante Varianz anzeigt:

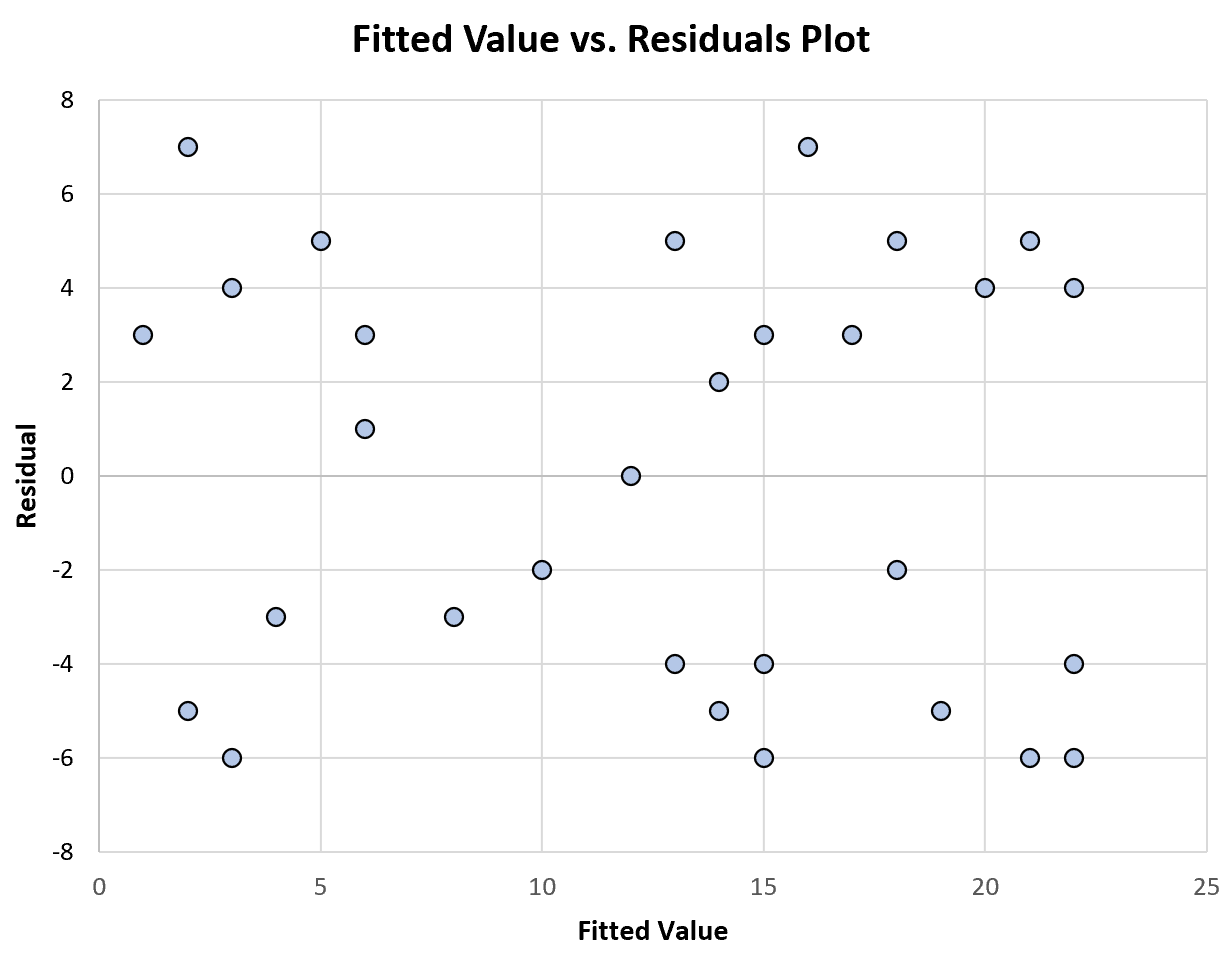
Beachten Sie, dass die Residuen in keinem bestimmten Muster zufällig um Null herum verstreut sind und auf jeder Ebene der angepassten Werte eine annähernd konstante Varianz aufweisen.

Das folgende Diagramm zeigt ein Beispiel für ein Diagramm angepasster Werte gegenüber Residuen, das eine nicht konstante Varianz anzeigt:

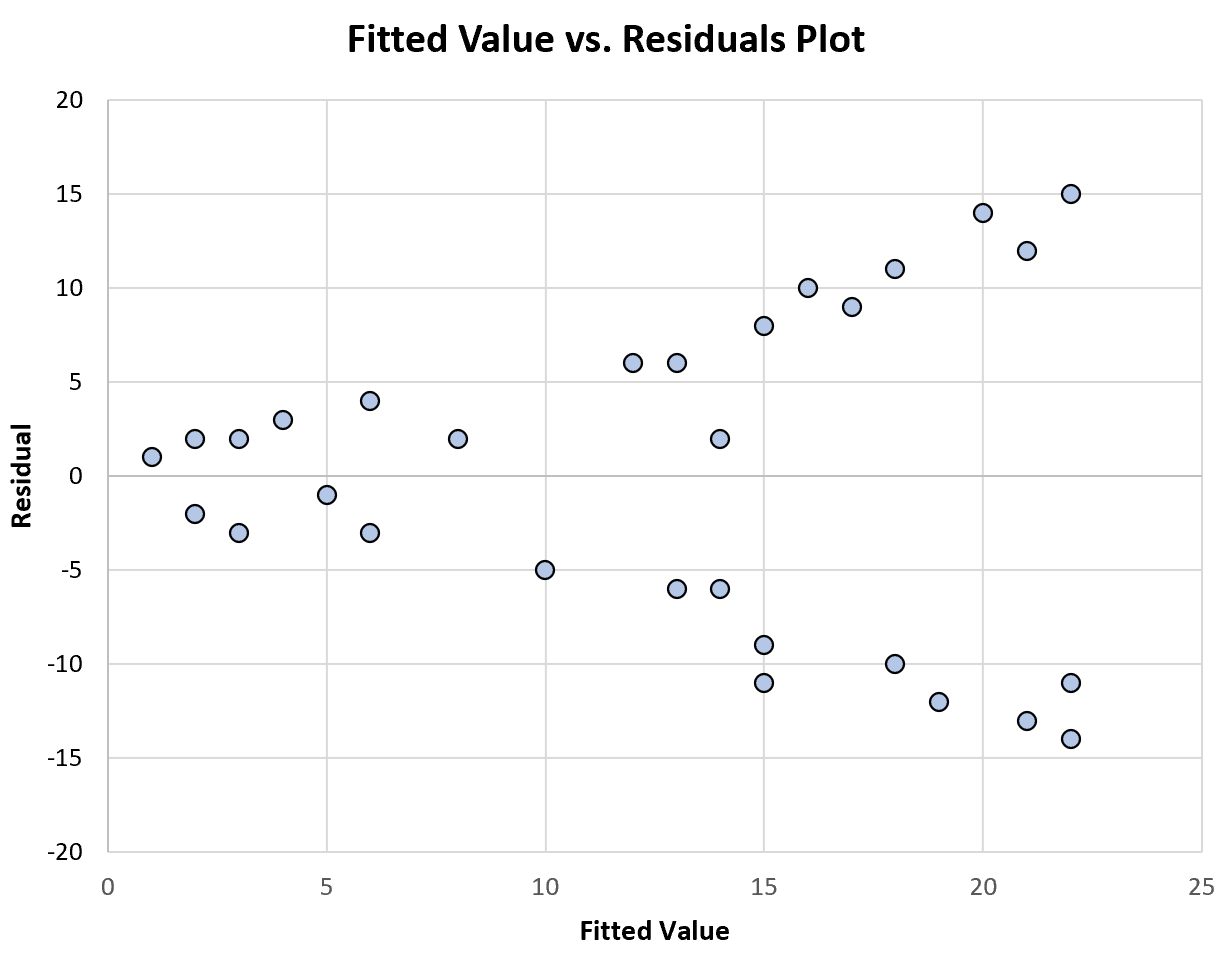
Beachten Sie, dass die Verteilung der Residuen mit zunehmenden angepassten Werten größer wird. Dies ist ein typisches Zeichen einer nicht konstanten Varianz.

Dies zeigt uns, dass unser Regressionsmodell unter einer nicht konstanten Varianz der Residuen leidet und dass die Schätzungen der Modellkoeffizienten daher unzuverlässig sind.

So beheben Sie einen Verstoß gegen die konstante Varianz

Wenn die Annahme einer konstanten Varianz verletzt wird, besteht die häufigste Lösung dieses Problems darin, die Antwortvariable mithilfe einer von drei Transformationen zu transformieren:

1. Log-Transformation: Transformieren Sie die Antwortvariable von y in log(y)

2. Quadratwurzeltransformation: Transformieren Sie die Antwortvariable von y in √y

3. Kubikwurzeltransformation: Transformieren Sie die Antwortvariable von y in y ^1/3

Durch die Durchführung dieser Transformationen verschwindet im Allgemeinen das Problem der nicht konstanten Varianz.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zur linearen Regression und Residuenanalyse:

Einführung in die einfache lineare Regression
Einführung in die multiple lineare Regression
Die vier Annahmen der linearen Regression
Was sind Residuen in der Statistik?