So führen sie eine verschachtelte anova in r durch (schritt für schritt)

Eine verschachtelte ANOVA ist eine Art ANOVA („Varianzanalyse“), bei der mindestens ein Faktor in einem anderen Faktor verschachtelt ist.

Angenommen, ein Forscher möchte wissen, ob drei verschiedene Düngemittel ein unterschiedliches Pflanzenwachstum bewirken.

Um dies zu testen, streuen drei verschiedene Techniker jeweils Dünger A auf vier Pflanzen, drei weitere Techniker streuen jeweils Dünger B auf vier Pflanzen und drei weitere Techniker streuen jeweils Dünger C auf vier Pflanzen.

In diesem Szenario ist die Reaktionsvariable das Pflanzenwachstum und die beiden Faktoren Technik und Dünger. Es stellt sich heraus, dass der Techniker im Dünger steckt :

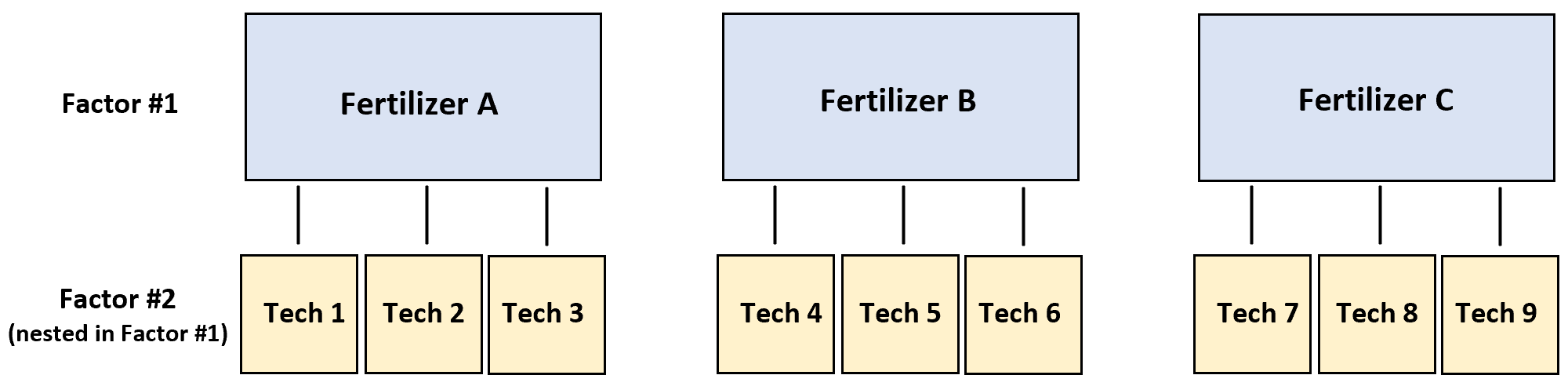
Das folgende Schritt-für-Schritt-Beispiel zeigt, wie diese verschachtelte ANOVA in R durchgeführt wird.

Schritt 1: Erstellen Sie die Daten

Erstellen wir zunächst einen Datenrahmen, um unsere Daten in R zu speichern:

 #create data
df <- data. frame (growth=c(13, 16, 16, 12, 15, 16, 19, 16, 15, 15, 12, 15,
                          19, 19, 20, 22, 23, 18, 16, 18, 19, 20, 21, 21,
                          21, 23, 24, 22, 25, 20, 20, 22, 24, 22, 25, 26),
                 fertilizer=c(rep(c(' A ', ' B ', ' C '), each= 12 )),
                 tech=c(rep(1:9, each= 4 )))

#view first six rows of data
head(df)

  growth fertilizer tech
1 13 A 1
2 16 A 1
3 16 A 1
4 12 A 1
5 15 A 2
6 16 A 2

Schritt 2: Passen Sie die verschachtelte ANOVA an

Wir können die folgende Syntax verwenden, um eine verschachtelte ANOVA in R anzupassen:

aov(Antwort ~ Faktor A / Faktor B)

Gold:

• Antwort: die Antwortvariable
• Faktor A: der erste Faktor
• Faktor B: der zweite Faktor, der im ersten Faktor verschachtelt ist

Der folgende Code zeigt, wie die verschachtelte ANOVA für unseren Datensatz angepasst wird:

 #fit nested ANOVA
nest <- aov(df$growth ~ df$fertilizer / factor(df$tech))

#view summary of nested ANOVA
summary(nest)

                              Df Sum Sq Mean Sq F value Pr(>F)    
df$fertilizer 2 372.7 186.33 53.238 4.27e-10 ***
df$fertilizer:factor(df$tech) 6 31.8 5.31 1.516 0.211    
Residuals 27 94.5 3.50                     
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Schritt 3: Interpretieren Sie das Ergebnis

Wir können uns die p-Wert-Spalte ansehen, um zu bestimmen, ob jeder Faktor einen statistisch signifikanten Einfluss auf das Pflanzenwachstum hat oder nicht.

Aus der obigen Tabelle können wir ersehen, dass Düngemittel einen statistisch signifikanten Einfluss auf das Pflanzenwachstum haben (p-Wert < 0,05), der Techniker jedoch nicht (p-Wert = 0,211).

Das zeigt uns, dass wir uns, wenn wir das Pflanzenwachstum steigern wollen, auf den verwendeten Dünger konzentrieren müssen und nicht auf den einzelnen Techniker, der den Dünger ausbringt.

Schritt 4: Visualisieren Sie die Ergebnisse

Schließlich können wir Boxplots verwenden, um die Verteilung des Pflanzenwachstums nach Düngemitteln und nach Technikern zu visualisieren:

 #load ggplot2 data visualization package
library (ggplot2)

#create boxplots to visualize plant growth
ggplot(df, aes (x=factor(tech), y=growth, fill=fertilizer)) +
  geom_boxplot()

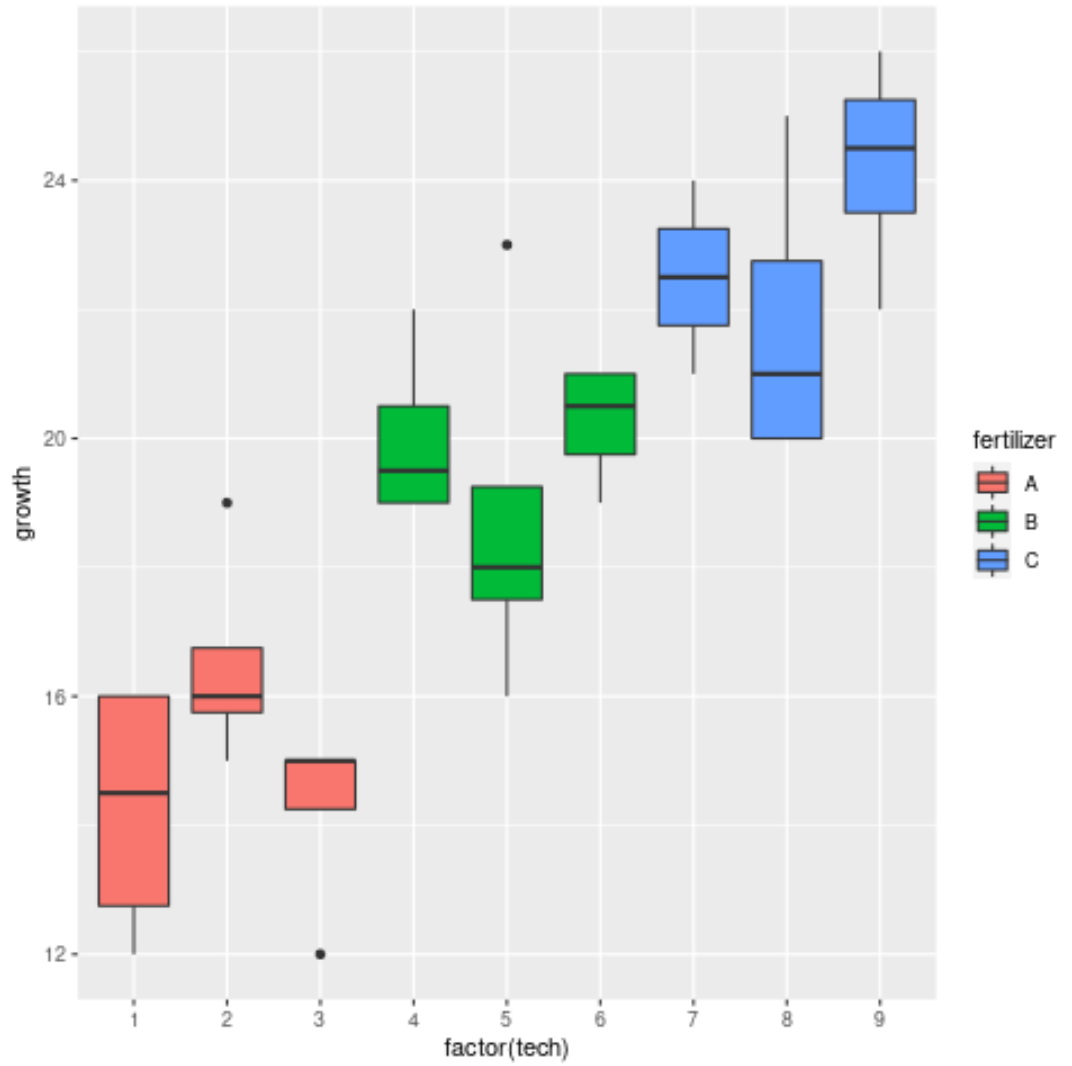
Die Grafik zeigt, dass es erhebliche Wachstumsunterschiede zwischen den drei verschiedenen Düngemitteln gibt, jedoch nicht so große Unterschiede zwischen den Technikern innerhalb jeder Düngemittelgruppe.

Dies scheint mit den Ergebnissen der verschachtelten ANOVA übereinzustimmen und bestätigt, dass Düngemittel einen signifikanten Einfluss auf das Pflanzenwachstum haben, einzelne Techniker jedoch nicht.

Zusätzliche Ressourcen

So führen Sie eine einfaktorielle ANOVA in R durch
So führen Sie eine zweifaktorielle ANOVA in R durch
So führen Sie eine ANOVA mit wiederholten Messungen in R durch