Anova mit oder ohne replikation: was ist der unterschied?

Eine zweifaktorielle ANOVA wird verwendet, um zu bestimmen, ob zwei Prädiktorvariablen (oder „Faktoren“) einen statistisch signifikanten Einfluss auf eine Antwortvariable haben.

Es gibt zwei verschiedene Arten von Zwei-Wege-ANOVA-Modellen:

1. Zweifaktorielle ANOVA ohne Replikation

• Für jede Stufenkombination der Prädiktorvariablen gibt es nur eine Beobachtung .

2. Zweifaktorielle ANOVA mit Replikation

• Für jede Kombination von Ebenen für die Prädiktorvariablen gibt es mehrere Beobachtungen .

Ein Botaniker möchte beispielsweise wissen, ob Sonneneinstrahlung (Keine, Niedrig, Mittel, Hoch) und die Bewässerungshäufigkeit (Täglich, Wöchentlich) einen statistisch signifikanten Einfluss auf das Pflanzenwachstum haben.

Sie könnte eines der folgenden Zwei-Wege-ANOVA-Modelle durchführen:

1. Zweifaktorielle ANOVA ohne Replikation

Mit diesem Ansatz würde der Botaniker das Wachstum einer Pflanze nur für jede Kombination aus Sonneneinstrahlung und Bewässerungshäufigkeit messen.

Beispielsweise wurde das Wachstum einer Pflanze gemessen, die keinem Sonnenlicht ausgesetzt war und täglich gegossen wurde.

Als nächstes maß sie das Wachstum einer einzelnen Pflanze ohne Sonneneinstrahlung und wöchentliches Gießen.

Und so weiter.

Die folgende Tabelle zeigt, wie eine zweifaktorielle ANOVA ohne Replikation aussehen könnte:

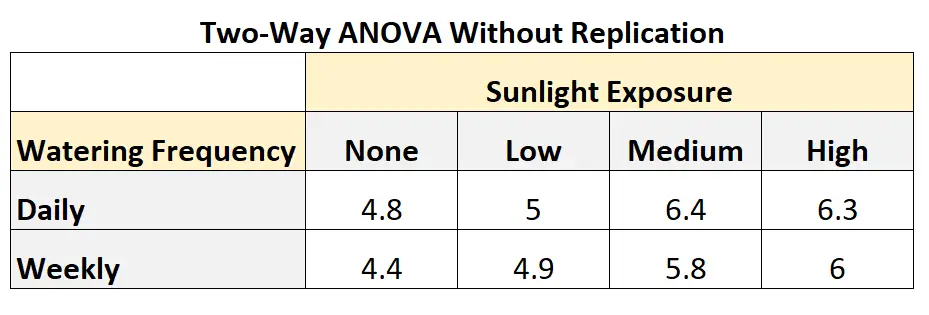
Aus der Tabelle können wir sehen:

• Die Pflanze, die keinem Sonnenlicht ausgesetzt war und täglich gegossen wurde, hatte ein Wachstum von 4,8 Zoll.
• Die Pflanze ohne Sonneneinstrahlung und ohne wöchentliches Gießen hatte ein Wachstum von 4,4 Zoll.
• Die Pflanze, die wenig Sonnenlicht ausgesetzt war und täglich gegossen wurde, wuchs um 5 Zoll.
• Die Pflanze, die wenig Sonnenlicht ausgesetzt war und wöchentlich gegossen wurde, wuchs um 4,9 Zoll.

Und so weiter.

2. Zweifaktorielle ANOVA mit Replikation

Mit diesem Ansatz würde der Botaniker das Wachstum mehrerer Pflanzen für jede Kombination aus Sonneneinstrahlung und Bewässerungshäufigkeit messen.

Es könnte beispielsweise das Wachstum von fünf verschiedenen Pflanzen messen, die keinem Sonnenlicht ausgesetzt sind und täglich gegossen werden.

Als nächstes maß sie das Wachstum von fünf anderen Pflanzen ohne Sonneneinstrahlung und ohne wöchentliches Gießen.

Und so weiter.

Die folgende Tabelle zeigt, wie eine zweifaktorielle ANOVA mit Replikation aussehen könnte:

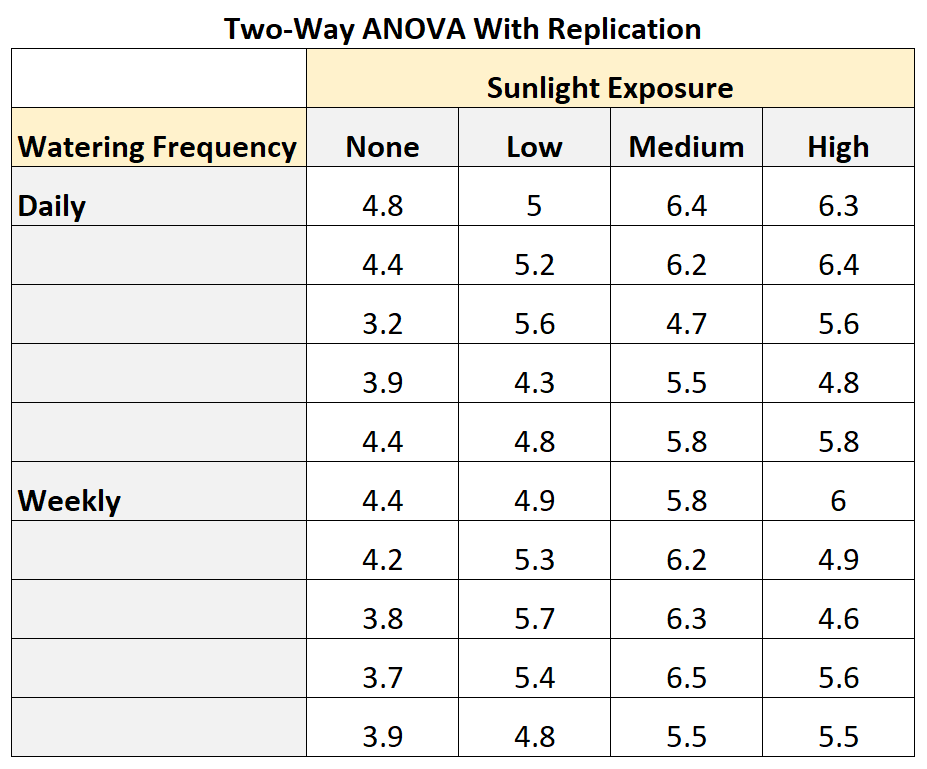
Aus der Tabelle können wir sehen:

• Eine Pflanze ohne Sonneneinstrahlung und tägliches Gießen hatte ein Wachstum von 4,8 Zoll.
• Eine andere Pflanze, die keinem Sonnenlicht ausgesetzt war und täglich gegossen wurde, hatte ein Wachstum von 4,4 Zoll.
• Eine andere Pflanze, die keinem Sonnenlicht ausgesetzt war und täglich gegossen wurde, hatte ein Wachstum von 8,1 cm.

Und so weiter.

Der Unterschied zwischen ANOVA mit und ohne Replikation

Der größte Unterschied zwischen einem ANOVA-Modell mit Replikation und einem ANOVA-Modell ohne Replikation besteht darin, dass es nur möglich ist, den Interaktionseffekt zwischen den beiden Prädiktorvariablen in einer ANOVA mit Replikation zu messen .

Ein Interaktionseffekt bedeutet, dass zwischen den beiden Prädiktorvariablen eine Art Interaktion besteht, die sich darauf auswirken kann, wie wir die Beziehung zwischen den Prädiktorvariablen und der Antwortvariablen interpretieren.

Der Botaniker möchte beispielsweise wissen, ob Sonneneinstrahlung und die Häufigkeit des Gießens das Pflanzenwachstum beeinflussen.

Obwohl es möglich ist, dass diese beiden Prädiktorvariablen das Pflanzenwachstum beeinflussen, ist es auch möglich, dass sie miteinander interagieren.

Beispielsweise ist es möglich, dass Pflanzen durch Sonneneinstrahlung unterschiedlich schnell wachsen, je nachdem, ob eine Pflanze täglich oder wöchentlich gegossen wird.

In diesem Fall besteht ein Wechselwirkungseffekt zwischen Sonneneinstrahlung und Bewässerungshäufigkeit.

Die einzige Möglichkeit, einen Interaktionseffekt zu messen, besteht jedoch darin, für jede Ebenenkombination der Prädiktorvariablen mehrere Messwerte zu verwenden.

ANOVA mit und ohne Replikation in Excel

Wenn wir in Excel eine zweifaktorielle ANOVA ohne Replikation durchführen, sieht das Ergebnis wie folgt aus:

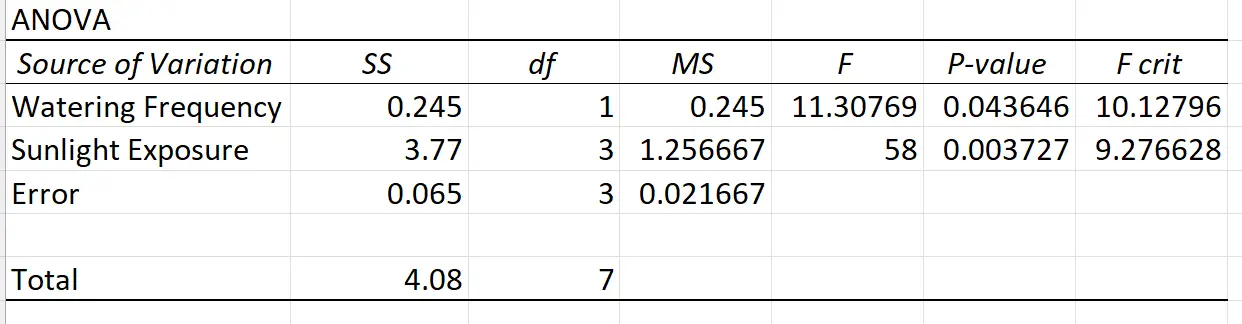
Da die p-Werte in der ANOVA-Tabelle für Sonneneinstrahlung und Bewässerungshäufigkeit unter 0,05 liegen, würden wir daraus schließen, dass beide Variablen einen statistisch signifikanten Einfluss auf das Pflanzenwachstum haben.

Beachten Sie jedoch, dass in der ANOVA-Tabelle keine Interaktionsterme enthalten sind, sodass wir nicht wissen, ob zwischen den beiden Prädiktorvariablen ein Interaktionseffekt besteht.

Wenn wir andererseits eine zweifaktorielle ANOVA mit Replikation in Excel durchführen, sieht das Ergebnis wie folgt aus:

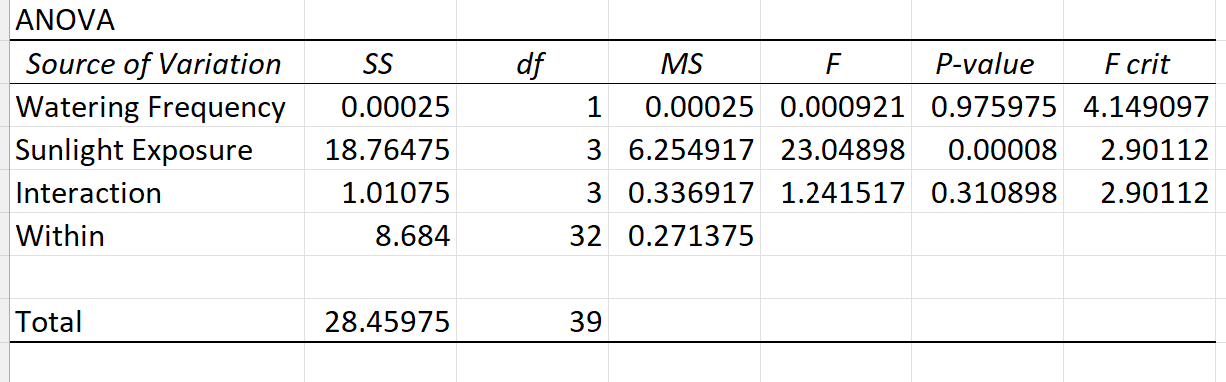
Beachten Sie, dass diese ANOVA-Tabelle p-Werte für Sonneneinstrahlung, Bewässerungshäufigkeit und den Interaktionseffekt zwischen diesen beiden Prädiktorvariablen enthält.

Aus der Tabelle können wir ersehen, dass die Bewässerungshäufigkeit statistisch nicht signifikant ist, die Sonneneinstrahlung statistisch signifikant ist und es keinen Interaktionseffekt zwischen den beiden Vorhersagevariablen gibt, der statistisch nicht signifikant ist.

Dies bedeutet, dass wir unabhängig von der Bewässerungshäufigkeit Rückschlüsse auf die Auswirkungen der Sonneneinstrahlung auf das Pflanzenwachstum ziehen können.

Verwandte Themen: So führen Sie eine zweifaktorielle ANOVA in Excel durch

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zu zweifaktoriellen ANOVA-Modellen:

So führen Sie manuell eine zweifaktorielle ANOVA durch
So melden Sie Ergebnisse der Zwei-Wege-ANOVA
So interpretieren Sie F-Werte in einer zweifaktoriellen ANOVA