So führen sie eine einfaktorielle anova auf einem ti-84-rechner durch

Eine einfaktorielle ANOVA wird verwendet, um zu bestimmen, ob ein statistisch signifikanter Unterschied zwischen den Mittelwerten von drei oder mehr unabhängigen Gruppen besteht.

In diesem Tutorial wird erläutert, wie Sie eine einfaktorielle ANOVA auf einem TI-84-Rechner durchführen.

Beispiel: Einfaktorielle ANOVA auf einem TI-84-Rechner

Angenommen, wir rekrutieren 30 Studenten für die Teilnahme an einer Studie. Den Studierenden wird nach dem Zufallsprinzip zugeteilt, dass sie einen Monat lang eine von drei Lerntechniken anwenden sollen, um sich auf eine Prüfung vorzubereiten. Am Ende des Monats absolvieren alle Schüler den gleichen Test.

Führen Sie die folgenden Schritte aus, um eine einfache ANOVA durchzuführen und zu bestimmen, ob die Durchschnittswerte in den drei Gruppen gleich sind.

Schritt 1: Geben Sie die Daten ein.

Zuerst geben wir die Datenwerte für die erklärende Variable und die Antwortvariable ein. Drücken Sie Stat und dann EDIT . Tragen Sie die folgenden Prüfungsergebnisse für Studierende ein, die die erste Lernmethode in Spalte L1, die zweite Lernmethode in Spalte L2 und die dritte Lernmethode in Spalte L3 verwendet haben:

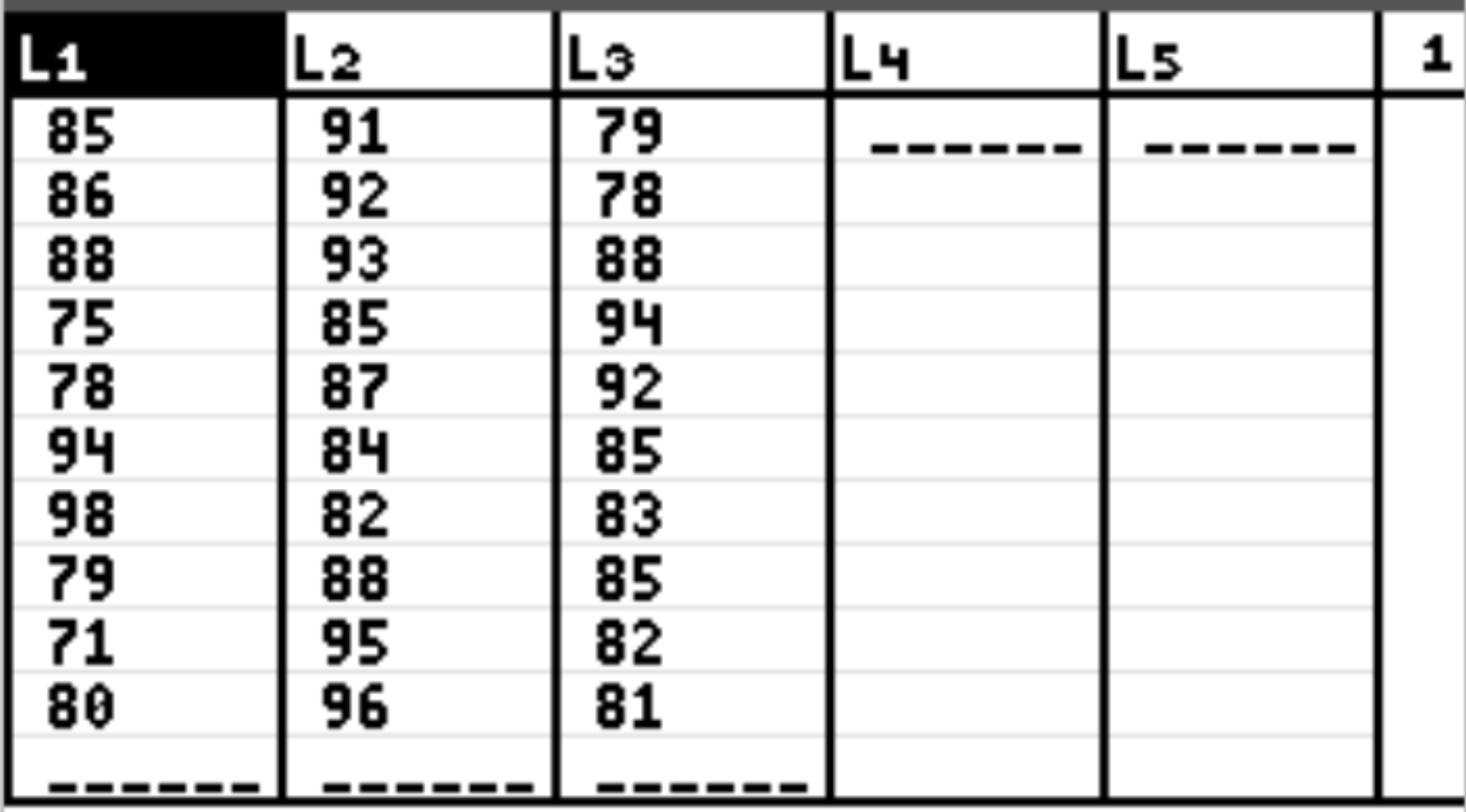
Schritt 2: Führen Sie eine einfaktorielle ANOVA durch.

Als nächstes führen wir die einfaktorielle ANOVA durch. Drücken Sie Stat und scrollen Sie dann zu TESTS . Scrollen Sie dann nach unten zu ANOVA und drücken Sie die Eingabetaste .

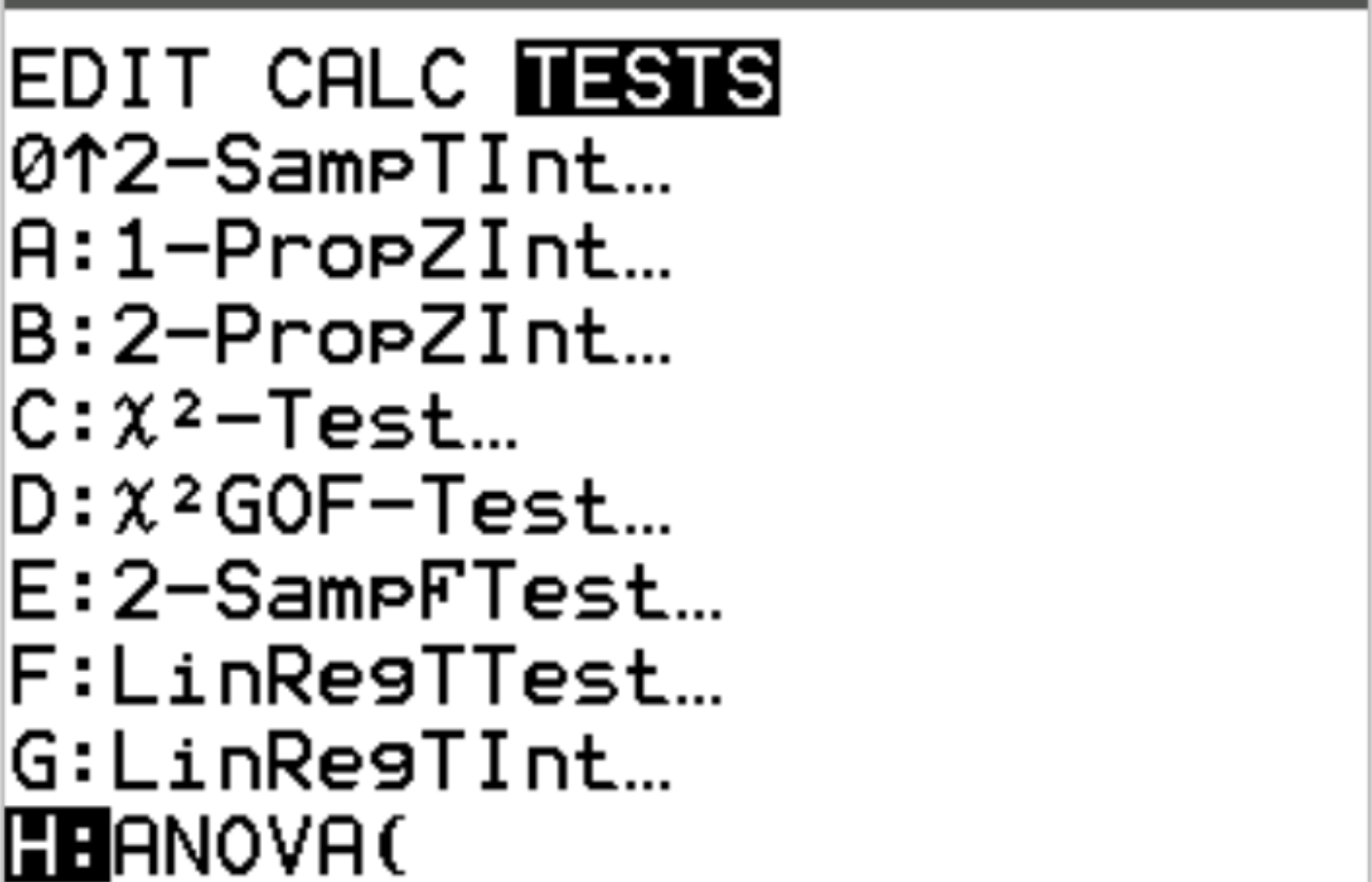
Geben Sie die Listen, in denen die Daten gespeichert sind, durch Kommas getrennt ein, fügen Sie dann eine schließende Klammer hinzu und drücken Sie dann die Eingabetaste .

Hinweis: Um L1 anzuzeigen, drücken Sie 2 und dann 1 . Um L2 aufzurufen, drücken Sie 2nd und dann 2 . Um L3 aufzurufen, drücken Sie 2nd und dann 3 .

Die folgenden Ergebnisse werden angezeigt, sobald Sie die Eingabetaste drücken:

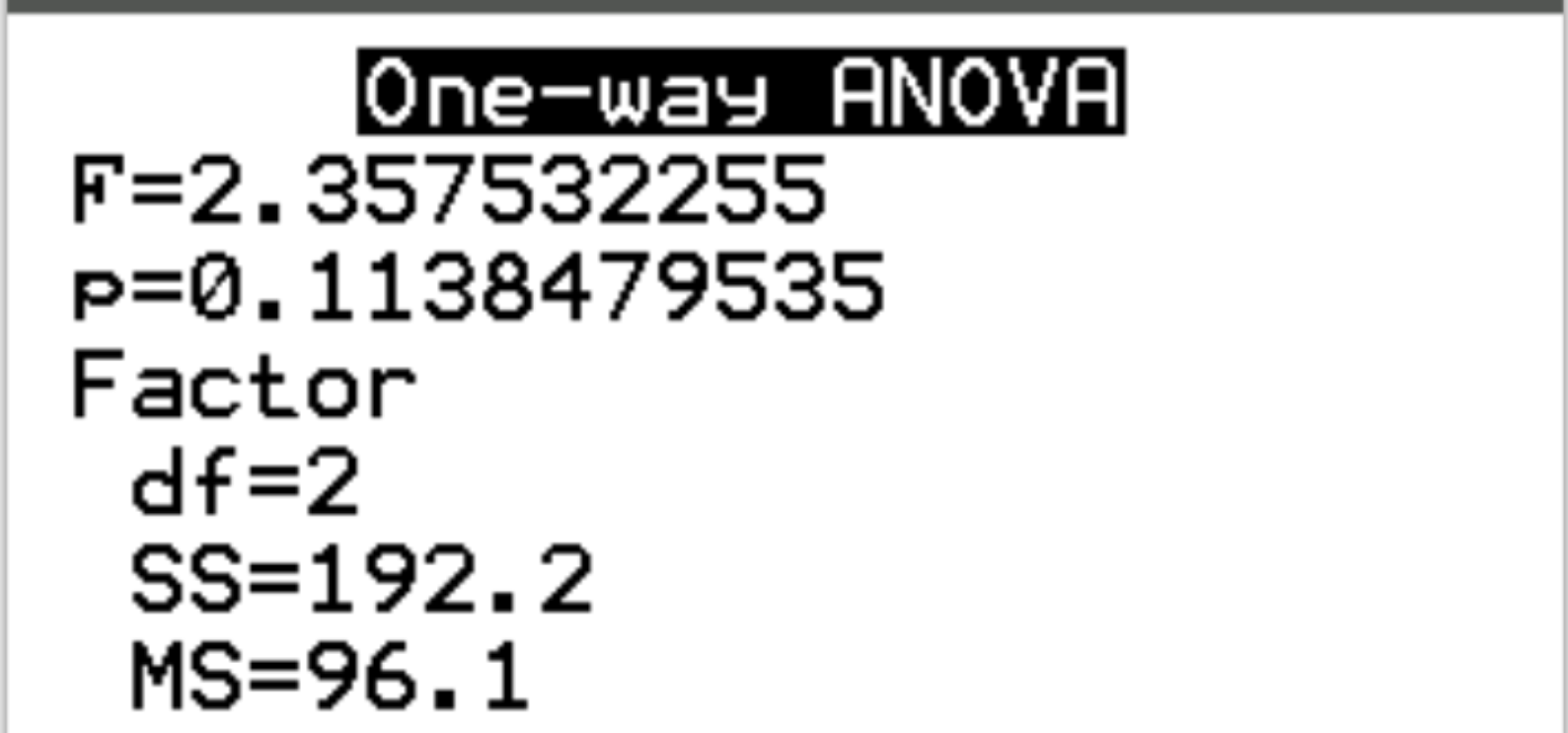
Schritt 3: Interpretieren Sie die Ergebnisse.

Die F-Statistik des Tests beträgt 2,3575 und der entsprechende p-Wert beträgt 0,1138 . Da dieser p-Wert nicht kleiner als 0,05 ist, können wir die Nullhypothese nicht ablehnen.

Daher liegen uns keine ausreichenden Beweise dafür vor, dass die durchschnittliche Prüfungspunktzahl zwischen den drei Gruppen unterschiedlich ist. Mit anderen Worten: Wir haben nicht genügend Beweise dafür, dass die Studientechnik zu unterschiedlichen Testergebnissen führt.