So führen sie eine anova mit ungleichen stichprobengrößen durch

Eine häufig gestellte Frage von Studierenden zum Thema Statistik lautet:

Ist es möglich, eine einfaktorielle ANOVA durchzuführen, wenn die Stichprobengrößen der einzelnen Gruppen nicht gleich sind?

Die kurze Antwort:

Ja, Sie können eine einfaktorielle ANOVA durchführen, wenn die Stichprobengrößen nicht gleich sind. Gleiche Stichprobengrößen gehören nicht zu den Annahmen einer ANOVA.

Bei der Durchführung einer einfaktoriellen ANOVA mit ungleichen Stichprobengrößen sind jedoch zwei potenzielle Probleme zu berücksichtigen:

(1) Reduzierte statistische Aussagekraft.

(2) Robustheit reduziert auf ungleiche Varianz.

In den folgenden Abschnitten werden diese beiden potenziellen Probleme ausführlich erläutert.

Problem Nr. 1: Reduzierte statistische Aussagekraft

Wenn wir irgendeine Art von statistischem Test verwenden, um Gruppen zu vergleichen, ist die statistische Aussagekraft des Tests am höchsten, wenn jede Gruppe die gleiche Stichprobengröße hat.

Denken Sie daran, dass sich die statistische Aussagekraft auf die Wahrscheinlichkeit bezieht, dass ein Test einen Effekt erkennt, wenn einer tatsächlich vorhanden ist.

Es kann gezeigt werden, dass die statistische Aussagekraft einer ANOVA umso geringer ist, je größer die Stichprobengrößenunterschiede zwischen den Gruppen sind.

Aus diesem Grund wünschen sich Forscher im Allgemeinen gleiche Stichprobengrößen, um eine höhere Trennschärfe und damit eine größere Wahrscheinlichkeit zu erreichen, echte Unterschiede zu erkennen.

Es ist sicherlich möglich, eine einfaktorielle ANOVA mit ungleichen Stichprobengrößen durchzuführen, Sie sollten sich jedoch darüber im Klaren sein, dass die Aussagekraft der einfaktoriellen ANOVA verringert wird.

Problem Nr. 2: Robustheit reduziert auf ungleiche Varianz

Eine der Annahmen einer einfaktoriellen ANOVA ist, dass die Varianz zwischen den einzelnen Gruppen gleich ist.

Im Allgemeinen gilt eine einfaktorielle ANOVA als robust gegenüber Verstößen gegen die Annahme gleicher Varianzen, jedoch nur, wenn jede Gruppe die gleiche Stichprobengröße hat .

Wenn Sie also ungleiche Stichprobengrößen und ungleiche Varianzen zwischen den Gruppen haben, kann es schwierig sein, den Ergebnissen der einfaktoriellen ANOVA zu vertrauen.

So entscheiden Sie, ob eine einfaktorielle ANOVA mit ungleichen Stichprobengrößen verwendet werden soll

Wenn Sie ungleiche Stichprobengrößen haben und eine einfaktorielle ANOVA durchführen möchten, um Unterschiede zwischen Gruppenmittelwerten zu testen, können Sie das folgende Flussdiagramm verwenden, um zu entscheiden, wie Sie vorgehen:

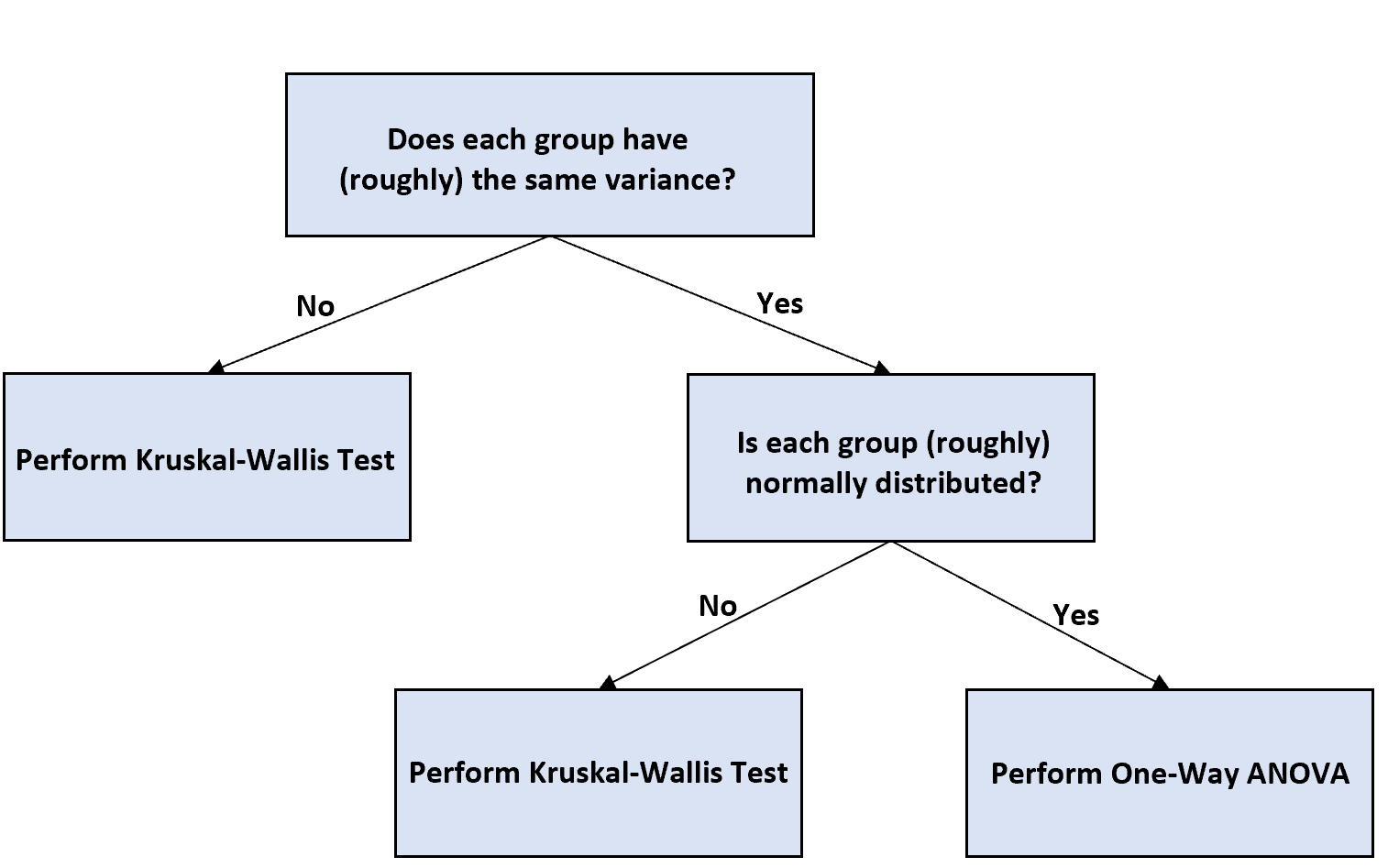
Hier ist eine kurze Erklärung des Flussdiagramms:

Schritt 1: Bestimmen Sie, ob jede Gruppe die gleiche Varianz aufweist.

Um festzustellen, ob jede Gruppe die gleiche Varianz aufweist, können Sie einen von zwei Ansätzen verwenden:

• Erstellen Sie Boxplots für jede Gruppe und prüfen Sie, ob die Werteverteilung in jeder Gruppe ungefähr gleich ist.
• Führen Sie einen formalen statistischen Test für gleiche Varianzen wie den Bartlett-Test durch.

Wenn die Varianzen nicht gleich sind, führen Sie einen Kruskal-Wallis-Test durch, der als nichtparametrisches Äquivalent einer einfaktoriellen ANOVA gilt.

Wenn die Lücken gleich sind, fahren Sie mit dem nächsten Schritt fort.

Schritt 2: Bestimmen Sie, ob jede Gruppe normalverteilt ist.

Um zu bestimmen, ob die Werte in jeder Gruppe ungefähr normalverteilt sind, können Sie einen von zwei Ansätzen verwenden:

• Erstellen Sie Histogramme oder QQ-Plots für jede Gruppe.
• Führen Sie formale statistische Tests wie Shapiro-Wilk, Kolmogorov-Smironov, Jarque-Barre oder D’Agostino-Pearson durch.

Wenn jede Gruppe normalverteilt ist, können Sie eine einfaktorielle ANOVA durchführen und die Ergebnisse wie jede normale einfaktorielle ANOVA interpretieren.

Wenn nicht jede Gruppe normalverteilt ist, führen Sie stattdessen einen Kruskal-Wallis-Test durch.

Zusätzliche Ressourcen

Eine Einführung in die einfaktorielle ANOVA
So überprüfen Sie ANOVA-Annahmen
Eine Einführung in den Kruskal-Wallis-Test
So interpretieren Sie den F-Wert und den P-Wert in der ANOVA