Anova mit wiederholten messungen: definition, formel und beispiel
Eine ANOVA mit wiederholten Messungen wird verwendet, um zu bestimmen, ob ein statistisch signifikanter Unterschied zwischen den Mittelwerten von drei oder mehr Gruppen besteht, in denen in jeder Gruppe dieselben Probanden vorkommen.
Eine ANOVA mit wiederholten Messungen wird im Allgemeinen in zwei spezifischen Situationen verwendet:
1. Messen Sie die durchschnittlichen Ergebnisse der Probanden über drei oder mehr Zeitpunkte. Beispielsweise möchten Sie möglicherweise die Ruheherzfrequenz der Probanden einen Monat vor Beginn eines Trainingsprogramms, in der Mitte des Trainingsprogramms und einen Monat nach dem Trainingsprogramm messen, um festzustellen, ob es einen signifikanten Unterschied in der durchschnittlichen Ruheherzfrequenz gibt. Zinssätze über diese drei Zeitpunkte.
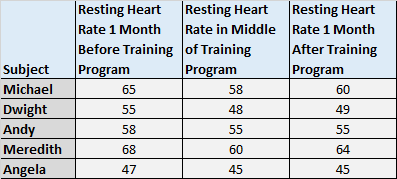
Beachten Sie, dass immer wieder dieselben Themen auftauchen. Wir haben dieselben Probanden wiederholt gemessen, weshalb wir eine ANOVA mit wiederholten Messungen verwendet haben.
2. Messen Sie die durchschnittlichen Ergebnisse der Probanden unter drei verschiedenen Bedingungen. Beispielsweise könnten Sie Probanden bitten, sich drei verschiedene Filme anzusehen und jeden davon danach zu bewerten, wie gut er ihnen gefallen hat.
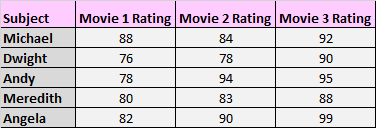
Auch hier treten in jeder Gruppe die gleichen Probanden auf, daher müssen wir eine ANOVA mit wiederholten Messungen verwenden, um den Mittelwertunterschied zwischen diesen drei Bedingungen zu testen.
Einfaktorielle ANOVA vs. ANOVA mit wiederholten Messungen
Bei einer typischen einfaktoriellen ANOVA werden in jeder Gruppe unterschiedliche Probanden verwendet. Wir könnten beispielsweise Probanden bitten, drei Filme zu bewerten, wie im Beispiel oben, aber wir verwenden unterschiedliche Probanden, um jeden Film zu bewerten:
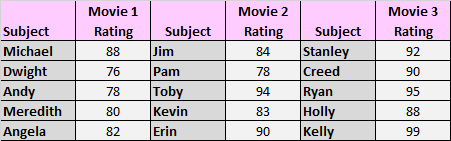
In diesem Fall würden wir eine typische einfaktorielle ANOVA durchführen, um den Unterschied zwischen den durchschnittlichen Bewertungen der drei Filme zu testen.
Im wirklichen Leben hat die Verwendung derselben Probanden unter verschiedenen Behandlungsbedingungen zwei Vorteile:
1. Für Forscher ist es kostengünstiger und schneller, eine kleinere Anzahl von Personen für die Durchführung eines Experiments zu rekrutieren und zu bezahlen, da sie die Daten einfach mehrmals von denselben Personen erhalten können.
2. Wir sind in der Lage, einen Teil der Varianz in den Daten den Probanden selbst zuzuschreiben, was es einfacher macht, einen kleineren p-Wert zu erhalten.
Ein potenzieller Nachteil dieser Art von Design besteht darin, dass die Probanden sich langweilen oder müde werden könnten, wenn ein Experiment zu lange dauert, was die Ergebnisse verfälschen könnte. Beispielsweise können Probanden den dritten Film, den sie ansehen, schlechter bewerten, weil sie müde und bereit sind, nach Hause zu gehen.
ANOVA mit wiederholten Messungen: Beispiel
Angenommen, wir rekrutieren fünf Probanden für die Teilnahme an einem Schulungsprogramm. Wir messen ihre Ruheherzfrequenz vor der Teilnahme an einem Trainingsprogramm, nach 4 Monaten Teilnahme und nach 8 Monaten Teilnahme.
Die folgende Tabelle zeigt die Ergebnisse:
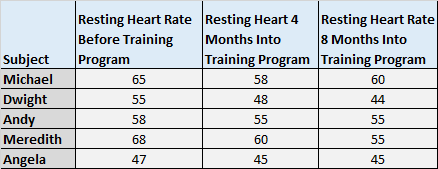
Wir möchten wissen, ob es zu diesen drei Zeitpunkten einen Unterschied in der durchschnittlichen verbleibenden Herzfrequenz gibt. Wir führen daher eine ANOVA mit wiederholten Messungen auf dem Signifikanzniveau 0,05 mit den folgenden Schritten durch:
Schritt 1. Formulieren Sie die Hypothesen.
Die Nullhypothese (H 0 ): µ 1 = µ 2 = µ 3 (Grundgesamtheitsmittelwerte sind alle gleich)
Die Alternativhypothese: (Ha): Mindestens ein Populationsmittelwert unterscheidet sich vom Rest
Schritt 2. Führen Sie eine ANOVA mit wiederholten Messungen durch.
Wir verwenden den ANOVA-Rechner mit wiederholten Messungen unter Verwendung der folgenden Eingabe:
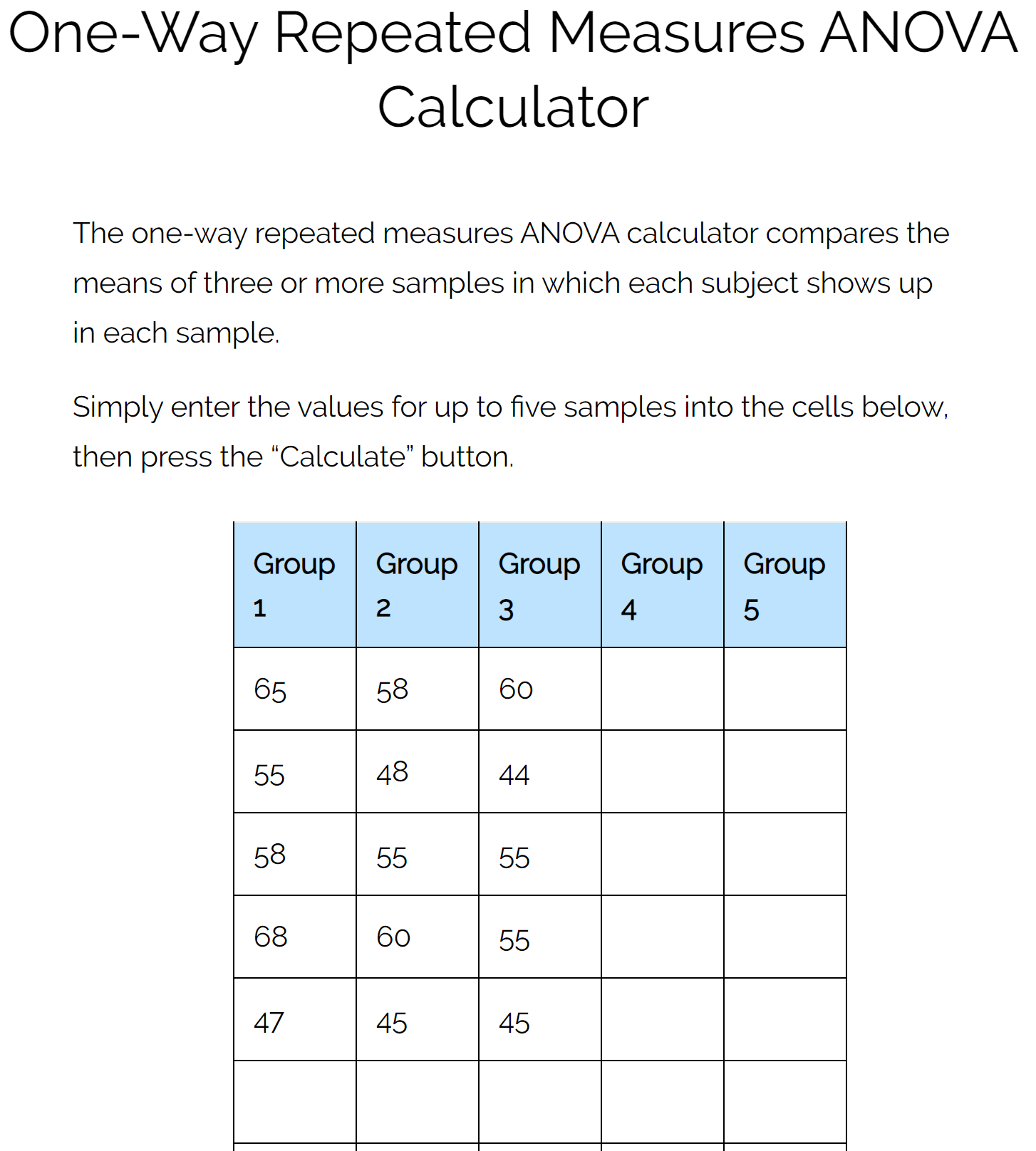
Sobald wir auf „Berechnen“ klicken, erscheint automatisch folgendes Ergebnis:
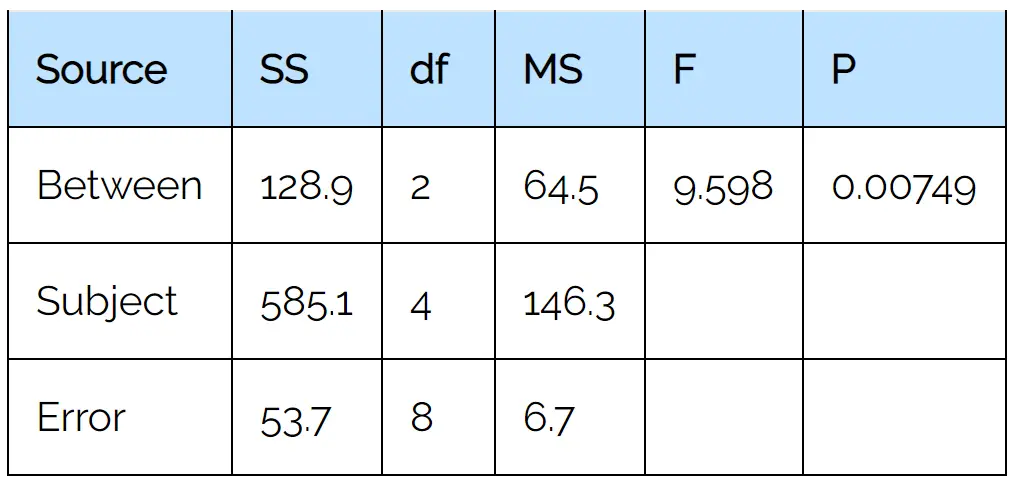
Schritt 3. Interpretieren Sie die Ergebnisse.
Aus der Ausgabetabelle sehen wir, dass die F-Teststatistik 9,598 und der entsprechende p-Wert 0,00749 beträgt.
Da dieser p-Wert kleiner als 0,05 ist, lehnen wir die Nullhypothese ab. Das bedeutet, dass wir genügend Beweise dafür haben, dass es einen statistisch signifikanten Unterschied zwischen der durchschnittlichen verbleibenden Herzfrequenz zu den drei verschiedenen Zeitpunkten gibt.
Zusätzliche Ressourcen
In den folgenden Artikeln wird erläutert, wie eine ANOVA mit wiederholten Messungen mit unterschiedlicher Statistiksoftware durchgeführt wird:
ANOVA mit wiederholten Messungen in Excel
ANOVA mit wiederholten Messungen in R
ANOVA mit wiederholten Messungen in Stata
ANOVA mit wiederholten Messungen in Python
ANOVA mit wiederholten Messungen in SPSS
ANOVA mit wiederholten Messungen in Google Sheets
Handwiederholungsmessungen ANOVA
ANOVA-Rechner für wiederholte Messungen