So führen sie manuell eine anova mit wiederholten messungen durch
Eine ANOVA mit wiederholten Messungen wird verwendet, um zu bestimmen, ob ein statistisch signifikanter Unterschied zwischen den Mittelwerten von drei oder mehr Gruppen besteht, in denen in jeder Gruppe dieselben Probanden vorkommen.
In diesem Tutorial wird erläutert, wie Sie eine einfaktorielle ANOVA mit wiederholten Messungen manuell durchführen.
Beispiel: Einfaktorielle ANOVA mit wiederholten Messungen von Hand
Forscher wollen wissen, ob drei verschiedene Medikamente unterschiedliche Reaktionszeiten verursachen. Um dies zu testen, messen sie die Reaktionszeit (in Sekunden) von fünf Patienten auf jedes Medikament. Die Ergebnisse sind unten dargestellt:
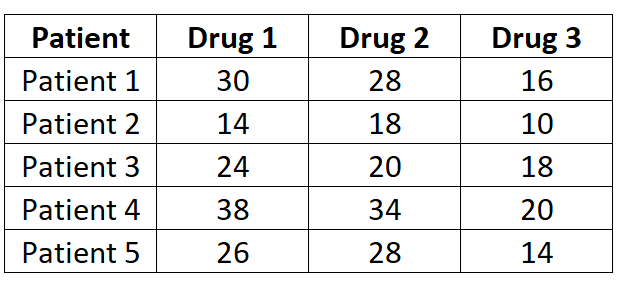
Da bei jedem Patienten jedes der drei Medikamente gemessen wird, verwenden wir eine einfaktorielle ANOVA mit wiederholten Messungen, um zu bestimmen, ob sich die mittlere Reaktionszeit zwischen den Medikamenten unterscheidet.
Befolgen Sie die folgenden Schritte, um eine ANOVA mit wiederholten Messungen manuell durchzuführen:
Schritt 1: Berechnen Sie den SST.
Zunächst berechnen wir die Gesamtquadratsumme (SST), die mit der folgenden Formel ermittelt werden kann:
SST = s 2 gesamt (n gesamt -1)
Gold:
- s 2 total : die Varianz für den Datensatz
- n total : die Gesamtzahl der Beobachtungen im Datensatz
In diesem Beispiel berechnen wir den SST wie folgt: (64,2667)(15-1) = 899,7
Schritt 2: SSB berechnen
Als nächstes berechnen wir die Quadratsumme (SSB), die mit der folgenden Formel ermittelt werden kann:
SSB = Σn j ( x j – x total ) 2
Gold:
- Σ : ein griechisches Symbol mit der Bedeutung „Summe“
- nj : die Gesamtzahl der Beobachtungen in der j- ten Gruppe
- x j : der Durchschnitt der j-ten Gruppe
- x total : der Durchschnitt aller Daten
In diesem Beispiel berechnen wir SSB wie folgt: (5)(26,4-22,533) 2 +(5)(25,6-22,533) 2 + (5)(15,6-22,533) 2 = 362,1
Schritt 3: Berechnen Sie den SSS.
Als nächstes berechnen wir die Subjektsumme der Quadrate (SSS), die mit der folgenden Formel ermittelt werden kann:
SSS =(Σr 2 k /c) – (N 2 /rc)
Gold:
- Σ : ein griechisches Symbol mit der Bedeutung „Summe“
- r 2 k : Quadratsumme des k-ten Patienten
- N: die Gesamtsumme aller Daten
- r: Gesamtzahl der Patienten
- c: Gesamtzahl der Gruppen
In diesem Beispiel berechnen wir SSS wie folgt: ((74 2 + 42 2 + 62 2 + 92 2 + 68 2 )/3) – (338 2 /(5)(3)) = 441,1
Schritt 4: SES berechnen.
Als nächstes berechnen wir die Summe der quadratischen Fehler (SSE), die mit der folgenden Formel ermittelt werden kann:
SSE = SST – SSB – SSS
In diesem Beispiel berechnen wir den SES wie folgt: 899,7 – 362,1 – 441,1 = 96,5
Schritt 5: Vervollständigen Sie die ANOVA-Tabelle mit wiederholten Messungen.
Nachdem wir nun SSB, SSS und SSE haben, können wir die ANOVA-Tabelle mit wiederholten Messungen füllen:
| Quelle | Summe der Quadrate (SS) | df | Mittlere Quadrate (MS) | F |
|---|---|---|---|---|
| Zwischen | 362.1 | 2 | 181.1 | 15.006 |
| Thema | 441.1 | 4 | 110.3 | |
| Fehler | 96,5 | 8 | 12.1 |
So haben wir die verschiedenen Zahlen in der Tabelle berechnet:
- df zwischen: #Gruppen – 1 = 3 – 1 = 2
- df-Betreff: #Teilnehmer – 1 = 5 – 1 = 4
- Fehler df: df zwischen * df subject = 2*4 = 8
- MS gibt ein: SSB / df gibt ein = 362,1 / 2 = 181,1
- MS-Fach: SSS-Fach / df = 441,1 / 4 = 110,3
- MS-Fehler: SSE-Fehler / df = 96,5 / 8 = 12,1
- F: MS gibt ein / MS-Fehler = 181,1 / 12,1 = 15,006
Schritt 6: Interpretieren Sie die Ergebnisse.
Die F-Teststatistik für diese einfaktorielle ANOVA mit wiederholten Messungen beträgt 15,006 . Um festzustellen, ob es sich hierbei um ein statistisch signifikantes Ergebnis handelt, müssen wir es mit dem kritischen F-Wert vergleichen, der in derF-Verteilungstabelle mit den folgenden Werten gefunden wird:
- α (Signifikanzniveau) = 0,05
- DF1 (Freiheitsgrade des Zählers) = df between = 2
- DF2 (Freiheitsgrade des Nenners) = Fehler df = 8
Wir stellen fest, dass der kritische Wert von F 4,459 beträgt.
Da die F-Teststatistik in der ANOVA-Tabelle größer ist als der kritische Wert F in der F-Verteilungstabelle, lehnen wir die Nullhypothese ab. Dies bedeutet, dass wir genügend Beweise haben, um zu sagen, dass es einen statistisch signifikanten Unterschied zwischen den durchschnittlichen Reaktionszeiten der Medikamente gibt.