Probenanteil
In diesem Artikel wird erläutert, was der Stichprobenanteil in der Statistik ist. So erfahren Sie, wie Sie den Stichprobenanteil berechnen, eine gelöste Aufgabe und auch, was der Unterschied zwischen dem Stichprobenanteil und dem Bevölkerungsanteil ist.
Wie hoch ist der Stichprobenanteil?
Der Stichprobenanteil ist das Verhältnis erfolgreicher Fälle in einer Stichprobe zur Stichprobengröße. Um den Stichprobenanteil zu berechnen, muss daher die Anzahl der Erfolge in der Stichprobe durch die Gesamtzahl der Daten geteilt werden.
Das Symbol für den Probenanteil ist
![]()
.
In der Statistik sind bei der Durchführung einer Befragung in der Regel nicht alle Bevölkerungsdaten bekannt, weshalb in der Regel eine Untersuchung einer repräsentativen Stichprobe durchgeführt und die daraus gezogenen Schlussfolgerungen dann auf die gesamte Bevölkerung hochgerechnet werden. Bevölkerung. Daher wird der Stichprobenanteil verwendet, um den Anteil an der Gesamtbevölkerung abzuschätzen. Im Folgenden werden wir sehen, wie das geht.
Beispiel für eine Proportionsformel
Der Stichprobenanteil entspricht der Anzahl erfolgreicher Fälle in der Stichprobe dividiert durch die Stichprobengröße. Daher lautet die Formel zur Berechnung des Stichprobenanteils :
![]()
Gold:
-

ist der Stichprobenanteil.
-

ist die Anzahl der erfolgreichen Fälle in der Stichprobe.
-

ist die Gesamtzahl der Datenelemente in der Stichprobe.
Beispiel für die Berechnung des Probenanteils
Nachdem wir die Definition des Stichprobenanteils und seine Formel kennengelernt haben, lösen wir in diesem Abschnitt ein einfaches Beispiel, damit Sie sehen können, wie der Stichprobenanteil berechnet wird.
- Ein Unternehmen stellt ein Spielzeug her und kauft eines seiner Teile von einem anderen externen Unternehmen. Da jedoch in den von ihm gekauften Chargen fehlerhafte Teile auftauchen, beschließt er, eine statistische Studie durchzuführen, um den Anteil der Teile in gutem Zustand und den Anteil der Mängel zu ermitteln. Sie bestellen also ein Muster von 1.000 Einheiten und finden 138 defekte Teile. Wie hoch ist der Anteil an Teilen in gutem Zustand in der Stichprobe? Und wie hoch ist der Anteil fehlerhafter Teile in der Stichprobe?
Die Anzahl der unbeschädigten Teile in der Stichprobe beträgt 1000 minus der Anzahl der defekten Teile:
![]()
Um den Stichprobenanteil zu ermitteln, wenden wir die Formel an, die wir oben gesehen haben:
![]()
Der Anteil der Teile in gutem Zustand an der Stichprobe beträgt somit 86,2 %.
Andererseits entspricht der Anteil der fehlerhaften Teile eins minus dem Anteil der guten Teile:
![]()
Der Stichprobenanteil fehlerhafter Teile liegt somit bei 13,8 %.
Stichprobenanteil und Bevölkerungsanteil
Der Bevölkerungsanteil ist der Anteil der statistischen Bevölkerung. Das heißt, der Bevölkerungsanteil ist das Verhältnis der Erfolgsfälle einer untersuchten Bevölkerung im Verhältnis zu allen Elementen, die Teil dieser Bevölkerung sind.
Daher besteht der Unterschied zwischen dem nationalen Anteil und dem Bevölkerungsanteil darin, dass der nationale Anteil der Anteil der Fälle einer Mehrheit ist, während sich der Bevölkerungsanteil auf den Anteil der Fälle von Ereignissen bezieht, die alle Elemente der Bevölkerung berücksichtigen.
Zur Unterscheidung des Stichprobenanteils vom Bevölkerungsanteil werden diese durch unterschiedliche Symbole dargestellt. Das Symbol für den Probenanteil ist
![]()
, während das Symbol für den Bevölkerungsanteil ist
![]()
.
Im Allgemeinen kann der Bevölkerungsanteil nicht genau bestimmt werden, da in der Regel nicht alle Bevölkerungswerte bekannt sind. Stattdessen wird der Wert des Bevölkerungsanteils üblicherweise anhand eines Konfidenzintervalls mit der folgenden Formel geschätzt:
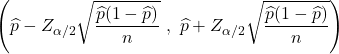
Um zu sehen, wie der Bevölkerungsanteil geschätzt wird, klicken Sie auf den folgenden Link:
Stichprobenverteilung der Anteile
Abschließend werden wir sehen, woraus eine Stichprobenverteilung der Anteile besteht, da es sich um ein statistisches Konzept handelt, das sich auf die Stichprobenanteile bezieht.
Beginnen wir zunächst damit, zu definieren, was eine Stichprobenverteilung ist. Eine Stichprobenverteilung ist die Verteilung, die sich aus der Berücksichtigung aller möglichen Stichproben aus einer statistischen Grundgesamtheit ergibt.
Daher ist eine Stichprobenverteilung der Anteile die Verteilung, die sich aus der Berechnung des Anteils jeder möglichen Stichprobe aus einer Grundgesamtheit ergibt. Das heißt, wenn wir alle möglichen Stichproben aus einer Grundgesamtheit untersuchen und den Anteil jeder Stichprobe berechnen, ist der berechnete Wertesatz eine Stichprobenverteilung der Stichprobenanteile.