Durchschnittliche typen (statistik)

Von Dr. Benjamin Anderson August 6, 2023 Statistiken Keine Kommentare

Hier erklären wir, was alle Arten von Durchschnittswerten in der Statistik sind und wie sie berechnet werden. Für jede Strumpfart finden Sie die Formel und Beispiele.

Aber bevor wir sehen, welche Arten von Durchschnittswerten es gibt, müssen wir logischerweise wissen, was ein Durchschnitt in der Statistik ist. Daher empfehlen wir Ihnen, den folgenden Link zu konsultieren, bevor Sie fortfahren.

➤ Siehe: Was ist der Durchschnitt (Statistik)?

Welche Arten von Durchschnittswerten gibt es in der Statistik?

In der Statistik gibt es folgende Arten von Durchschnittswerten:

Arithmetischer Durchschnitt
Gewichteter Durchschnitt
Geometrische Mittel
Wurzel bedeutet Quadrat
harmonische Bedeutung
verallgemeinerter Durchschnitt
verallgemeinerter f-Durchschnitt
getrimmt bedeutet
Interquartilmittelwert
Durchschnitt einer Funktion

Als nächstes erklären wir, wie man alle Arten von Durchschnittswerten in der Statistik berechnet. Die fünf am häufigsten verwendeten Durchschnittstypen sind der arithmetische Durchschnitt, der gewichtete Durchschnitt, der geometrische Durchschnitt, der quadratische Durchschnitt und der harmonische Durchschnitt. Deshalb gehen wir näher auf diese fünf Hauptmedientypen ein.

Arithmetischer Durchschnitt

Das arithmetische Mittel wird berechnet, indem alle Werte addiert und dann durch die Gesamtzahl der Datenpunkte dividiert werden.

Die Formel für das arithmetische Mittel lautet daher wie folgt:

$\displaystyle\overline{x}=\frac{1}{N}\sum_{i=1}^N x_i=\frac{x_1+x_2+\dots+x_N}{N}$

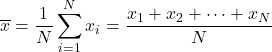
Das arithmetische Mittel wird auch als arithmetisches Mittel bezeichnet.

Der arithmetische Durchschnitt ist wahrscheinlich die am häufigsten verwendete Durchschnittsart in der Statistik.

Um ein Beispiel dafür zu sehen, wie diese Art von Durchschnitt ermittelt wird, berechnen wir den arithmetischen Durchschnitt der folgenden Daten:

$4\quad 7\quad 10\quad 1\quad 8\quad9$

Um das arithmetische Mittel zu berechnen, addieren Sie einfach alle statistischen Daten und dividieren Sie durch die Gesamtzahl der Daten, also 6:

$\overline{x}=\cfrac{4+7+10+1+8+9}{6}=6,5$

Gewichteter Durchschnitt

Um den gewichteten Durchschnitt zu berechnen, müssen Sie zunächst alle statistischen Daten mit ihrem Gewicht (oder Gewicht) multiplizieren, dann alle Produkte addieren und schließlich die gewichtete Summe durch die Summe aller Gewichte dividieren.

Die Formel für den gewichteten Durchschnitt lautet daher wie folgt:

$\overline{x_p}=\cfrac{\sum_{i=1}^N x_i\cdot w_i}{\sum_{i=1}^N w_i}=\cfrac{x_1\cdot w_1+x_2\cdot w_2+\dots x_N\cdot w_N}{w_1+w_2+\dosts +w_N}$

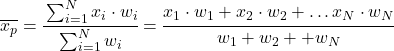
Dabei ist x _i der statistische Wert und w _i das entsprechende Gewicht.

Da der gewichtete Durchschnitt schwieriger zu verstehen ist, empfehlen wir Ihnen, sich das folgende Beispiel anzusehen, das Schritt für Schritt erklärt, wie er berechnet wird:

➤ Siehe: Beispiel für gewichteten Durchschnitt

Geometrische Mittel

Das geometrische Mittel einer Reihe statistischer Daten ist gleich der n-ten Wurzel des Produkts aller Werte.

Diese Art von Durchschnitt wird in der Unternehmensfinanzierung zur Berechnung von Renditen, prozentualen Durchschnittswerten und Zinseszinsen verwendet.

Die Formel für diese Art der Lagerung ist recht kompliziert. Tatsächlich kann der geometrische Mittelwert aller statistischen Sätze nicht berechnet werden, aber manchmal kann dieser Mittelwert nicht bestimmt werden. Aus diesem Grund empfehlen wir Ihnen, alle im folgenden Link erläuterten Ausnahmen zu konsultieren:

➤ Siehe: Geometrische Mittelformel

Wurzel bedeutet Quadrat

Der quadratische Mittelwert ist gleich der Quadratwurzel des arithmetischen Mittels der Quadrate der Daten.

Die mittlere quadratische Formel lautet daher wie folgt:

$\displaystyle RMS=\displaystyle\sqrt{\frac{1}{N}\sum_{i=1}^N x_i^2}=\sqrt{\frac{x_1^2+x_2^2+\dots + x_N^2}{N}\vphantom{\sum_{i=1}^N x_i^2}}}$

Diese Art des Durchschnitts wird auch Root Mean Square , Root Mean Square oder RMS genannt.

Wir möchten nur darauf hinweisen, dass es auch den kubischen Durchschnitt gibt, der jedoch in ganz besonderen Fällen verwendet wird.

Die quadratische Mittelung hat Vor- und Nachteile. Sie ist beispielsweise besonders nützlich, wenn die statistische Variable positive und negative Werte annimmt, da durch die Quadrierung jedes Datenelements alle Werte positiv werden. Weitere Funktionen dieses Medientyps können Sie sehen, indem Sie auf den folgenden Link klicken:

➤ Siehe: Vor- und Nachteile des quadratischen Mittelwerts

harmonische Bedeutung

Der harmonische Mittelwert wird berechnet, indem die Gesamtzahl der statistischen Daten durch die Summe der Kehrwerte jedes Werts dividiert wird.

$\displaystyle H=\frac{N}{\displaystyle\sum_{i=1}^N\frac{1}{x_i}}=\frac{N}{\displaystyle\frac{1}{x_1}+\frac{1}{x_2}+\dots+\frac{1}{x_N}}$

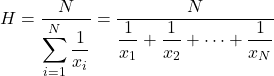
Der harmonische Durchschnitt wird zur Berechnung von Durchschnittsgeschwindigkeiten und -zeiten oder zur Durchführung elektronischer Berechnungen verwendet. Dieses Merkmal unterscheidet den harmonischen Durchschnitt von anderen Durchschnittstypen, die häufig bei der Berechnung von Preisdurchschnitten oder -prozentsätzen verwendet werden.

Beispiele zur Berechnung dieser Art von Durchschnitt finden Sie auf der folgenden Seite:

➤ Siehe: Beispiele für harmonische Bedeutung

Andere Arten von Strümpfen

In diesem Abschnitt sehen wir die Formeln für andere Arten von Strümpfen. Wir gehen nicht näher auf die einzelnen Arten von Strümpfen ein, da diese nicht weit verbreitet sind. Es ist jedoch gut für Sie zu wissen, dass es auch andere Arten von Strümpfen gibt.

Der verallgemeinerte Durchschnitt ist eine Mischung der oben genannten Durchschnittstypen und wird nach der folgenden Formel berechnet:

$\displaystyle\overline{x}(m) = \left ( \frac{1}{N}\cdot\sum_{i=1}^N{x_i^m} \right ) ^{1/m}$

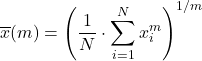
Sei f eine injektive und monotone Funktion, dann ist der verallgemeinerte f-Mittelwert definiert als:

$\displaystyle\overline{x} = f^{-1}\left({\frac{1}{N}\cdot\sum_{i=1}^N{f(x_i)}}\right)$

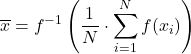
Beim getrimmten Mittelwert wird der arithmetische Mittelwert nach Abzug eines Prozentsatzes der Beobachtungen am oberen und unteren Ende der Stichprobe berechnet. Der gleiche Prozentsatz sollte an beiden Enden abgelehnt werden.

Um den Interquartil-Mittelwert , auch Interquartil-Mittelwert genannt, zu berechnen, werden zunächst die Daten des ersten und vierten Quartils verworfen und dann nur der arithmetische Mittelwert des zweiten und dritten Quartils der Stichprobe berechnet. Die Formel für diese Art von Durchschnitt lautet daher:

$\displaystyle\overline{x}={2 \over n} \sum_{i=\frac{n}{4}+1}^{\frac{3n}{4}}{x_i}$

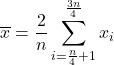
Schließlich können Sie auch den Mittelwert einer Funktion ermitteln. Der Durchschnittswert einer stetigen Funktion in einem geschlossenen Intervall [a,b] wird mit der folgenden Formel berechnet:

$\displaystyle\overline{f}=\frac{1}{b-a} \int_a^b f(t) dt$

Stichproben- und Bevölkerungsdurchschnitt

Schließlich werden wir sehen, was der Unterschied zwischen dem Stichprobendurchschnitt und dem Bevölkerungsdurchschnitt ist, zwei Arten von Durchschnittswerten, die oft verwechselt werden.

Der Stichprobenmittelwert ist der über die Werte einer statistischen Stichprobe berechnete Durchschnitt, das heißt, er wird über einen Teil aller Werte einer Variablen berechnet.

Der Bevölkerungsdurchschnitt ist der über eine statistische Grundgesamtheit, also über alle Werte einer Variablen, berechnete Durchschnitt. Daher stimmt der Populationsmittelwert mit der mathematischen Erwartung der Variablen überein.

Der Stichprobenmittelwert kann als praktisch gleich dem Grundgesamtheitsmittel angesehen werden, wenn eine ausreichend große Datenmenge bekannt ist. Der Wert des Grundgesamtheitsmittelwerts ist jedoch sehr schwer zu ermitteln, da in der Realität selten alle Werte einer Verteilung bekannt sind.

Über den Autor

Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen