So berechnen sie schiefe und kurtosis in google sheets

In der Statistik sind Schiefe und Kurtosis zwei Möglichkeiten, die Form einer Verteilung zu messen.

Schiefe ist ein Maß für die Schiefe einer Verteilung. Dieser Wert kann positiv oder negativ sein.

• Eine negative Schiefe zeigt an, dass sich das Ende auf der linken Seite der Verteilung befindet, die sich in Richtung negativerer Werte erstreckt.
• Eine positive Schiefe zeigt an, dass sich das Ende auf der rechten Seite der Verteilung befindet, die sich in Richtung positiverer Werte erstreckt.
• Ein Wert von Null zeigt an, dass die Verteilung keine Asymmetrie aufweist, was bedeutet, dass die Verteilung vollkommen symmetrisch ist.

Kurtosis ist ein Maß dafür, ob eine Verteilung im Vergleich zu einerNormalverteilung stark oder schwach ausgeprägt ist.

• Die Kurtosis einer Normalverteilung beträgt 3.
• Wenn eine bestimmte Verteilung eine Kurtosis von weniger als 3 aufweist, spricht man von einer Playkurtic- Verteilung, was bedeutet, dass sie tendenziell weniger und weniger extreme Ausreißer hervorbringt als die Normalverteilung.
• Wenn eine bestimmte Verteilung eine Kurtosis von mehr als 3 aufweist, spricht man von einer leptokurtischen Verteilung , was bedeutet, dass sie tendenziell mehr Ausreißer als die Normalverteilung hervorbringt.

In diesem Tutorial wird erläutert, wie Sie sowohl die Schiefe als auch die Kurtosis für einen bestimmten Datensatz in Google Sheets berechnen.

Beispiel: Schiefe und Abflachung in Google Sheets

Angenommen, wir haben den folgenden Datensatz:

Um die Schiefe und Kurtosis dieses Datensatzes zu berechnen, können wir die Funktionen SKEW() und KURT() mit der folgenden Syntax verwenden:

• SKEW (Wertetabelle)
• KURT (Wertetabelle)

Es ist wichtig zu beachten, dass jede Funktion den #DIV/0-Fehler zurückgibt! in den folgenden zwei Szenarien:

• Wenn weniger als drei Datenpunkte vorhanden sind.
• Wenn die Standardabweichung der Stichprobe Null ist.

Das Bild unten zeigt, wie diese Funktionen für unseren speziellen Datensatz verwendet werden:

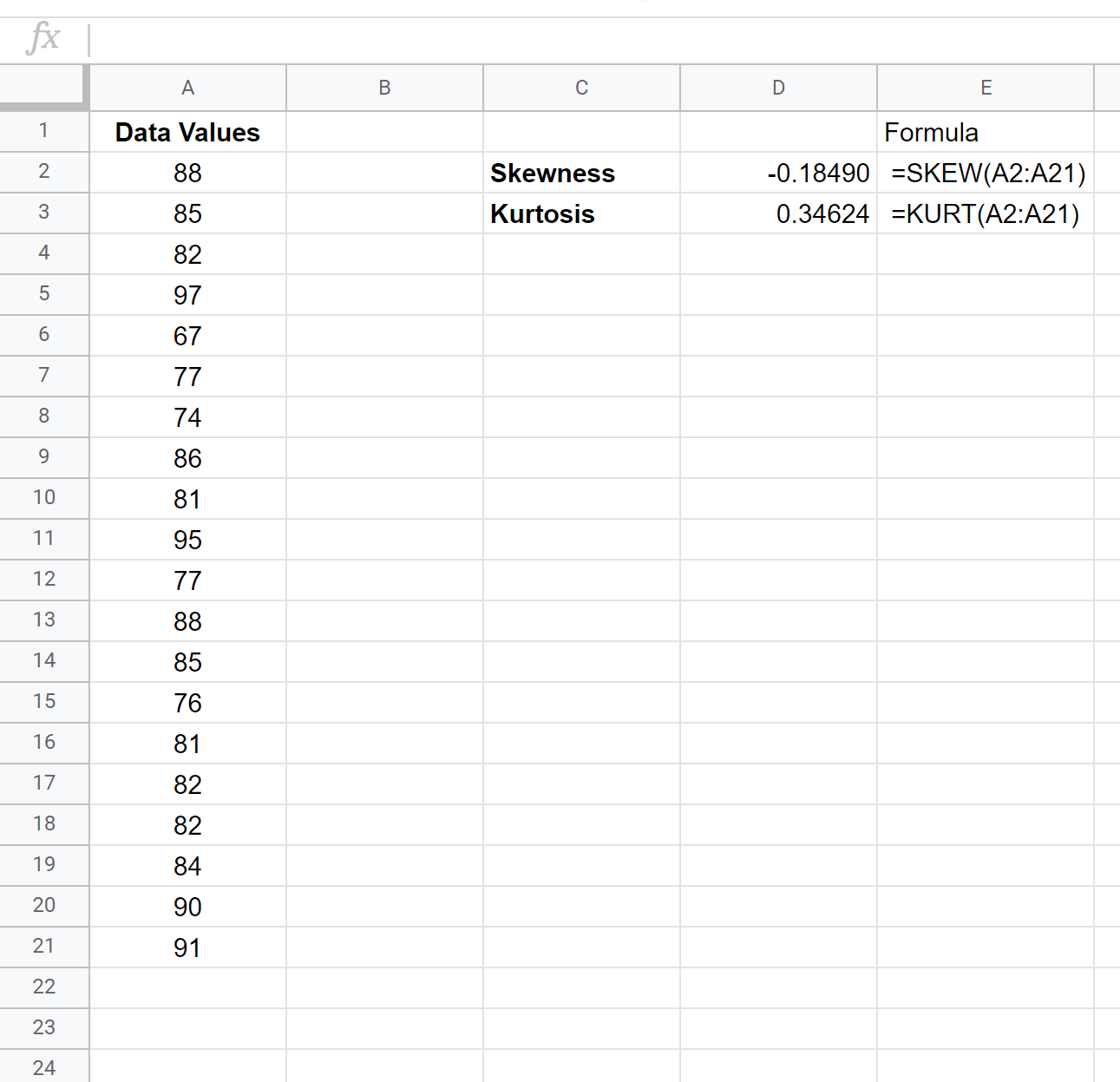
Die Schiefe beträgt -0,18490 und die Kurtosis 0,34624 .

Zusätzliche Ressource: Schiefe- und Kurtosis-Rechner

Sie können die Schiefe für einen bestimmten Datensatz auch mit dem Rechner für statistische Schiefe und Kurtosis berechnen , der automatisch Schiefe und Kurtosis für einen bestimmten Datensatz berechnet.