So berechnen sie schiefe und kurtosis in r

In der Statistik sind Schiefe und Kurtosis zwei Möglichkeiten, die Form einer Verteilung zu messen.

Schiefe ist ein Maß für die Schiefe einer Verteilung. Dieser Wert kann positiv oder negativ sein.

• Eine negative Schiefe zeigt an, dass sich das Ende auf der linken Seite der Verteilung befindet, die sich in Richtung negativerer Werte erstreckt.
• Eine positive Schiefe zeigt an, dass sich das Ende auf der rechten Seite der Verteilung befindet, die sich in Richtung positiverer Werte erstreckt.
• Ein Wert von Null zeigt an, dass die Verteilung keine Asymmetrie aufweist, was bedeutet, dass die Verteilung vollkommen symmetrisch ist.

Kurtosis ist ein Maß dafür, ob eine Verteilung im Vergleich zu einerNormalverteilung stark oder schwach ausgeprägt ist.

• Die Kurtosis einer Normalverteilung beträgt 3.
• Wenn eine bestimmte Verteilung eine Kurtosis von weniger als 3 aufweist, spricht man von einer Playkurtic- Verteilung, was bedeutet, dass sie tendenziell weniger und weniger extreme Ausreißer hervorbringt als die Normalverteilung.
• Wenn eine bestimmte Verteilung eine Kurtosis von mehr als 3 aufweist, spricht man von einer leptokurtischen Verteilung , was bedeutet, dass sie tendenziell mehr Ausreißer als die Normalverteilung hervorbringt.

Hinweis: Einige Formeln (Fisher-Definition) subtrahieren 3 von der Kurtosis, um den Vergleich mit der Normalverteilung zu erleichtern. Nach dieser Definition hätte eine Verteilung eine größere Kurtosis als eine Normalverteilung, wenn sie einen Kurtosis-Wert größer als 0 hätte.

In diesem Tutorial wird erklärt, wie sowohl die Schiefe als auch die Kurtosis eines bestimmten Datensatzes in R berechnet werden.

Beispiel: Schiefe und Abflachung in R

Angenommen, wir haben den folgenden Datensatz:

 data = c(88, 95, 92, 97, 96, 97, 94, 86, 91, 95, 97, 88, 85, 76, 68)

Wir können die Werteverteilung in diesem Datensatz schnell visualisieren, indem wir ein Histogramm erstellen:

 hist(data, col=' steelblue ') 

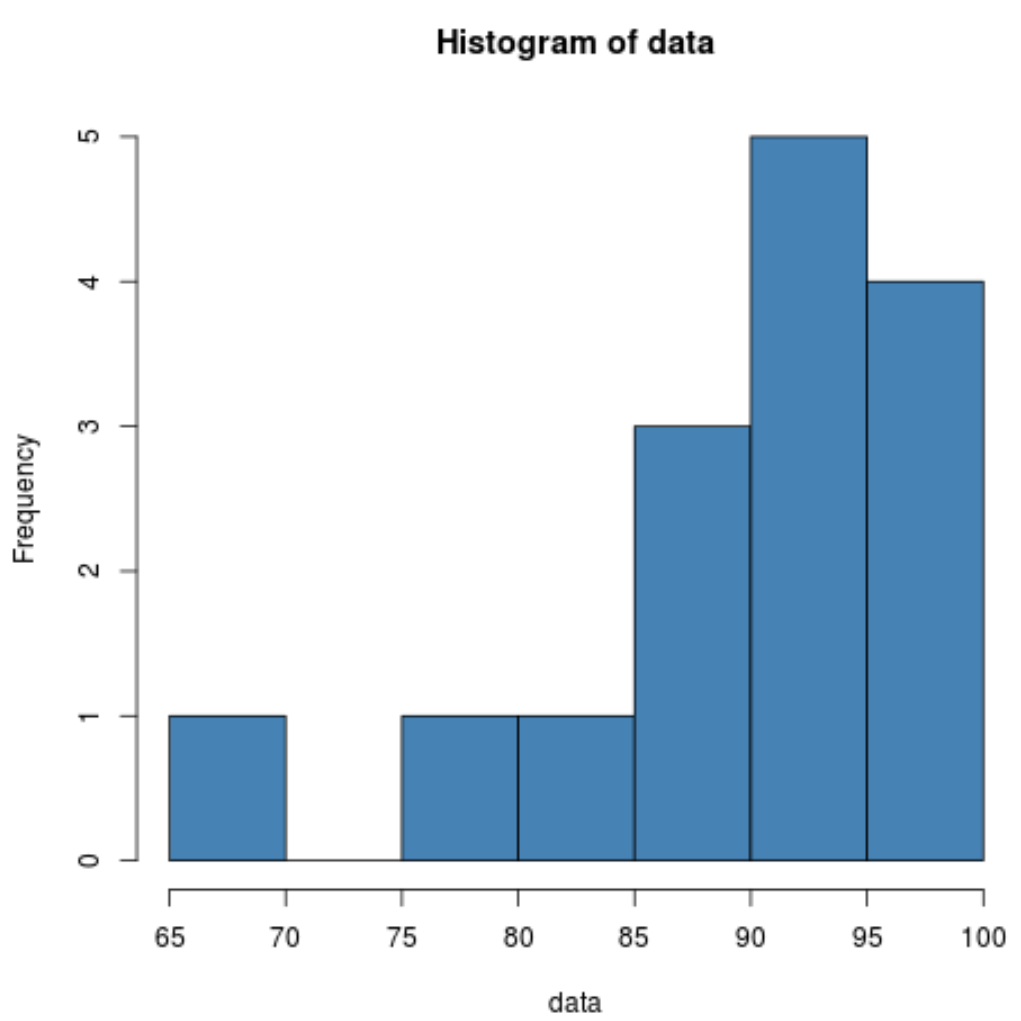
Das Histogramm zeigt uns, dass die Verteilung linksschief zu sein scheint. Das heißt, ein größerer Teil der Werte konzentriert sich auf der rechten Seite der Verteilung.

Um die Schiefe und Kurtosis dieses Datensatzes zu berechnen, können wir die Funktionen skewness() und kurtosis() aus der Momentenbibliothek in R verwenden:

 library (moments)

#calculate skewness
skewness(data)

[1] -1.391777

#calculate kurtosis
kurtosis(data)

[1] 4.177865

Die Schiefe beträgt -1,391777 und die Kurtosis 4,177865 .

Da die Schiefe negativ ist, deutet dies darauf hin, dass die Verteilung linksschief ist. Dies bestätigt, was wir im Histogramm gesehen haben.

Da die Kurtosis größer als 3 ist, weist dies darauf hin, dass die Verteilung im Vergleich zu einer Normalverteilung mehr Werte in den Enden aufweist.

Die Momentenbibliothek bietet auch die Funktion jarque.test() , die einen Anpassungstest durchführt, der bestimmt, ob die Beispieldaten Schiefe und Kurtosis aufweisen, die einer Normalverteilung entsprechen. Die Null- und Alternativhypothese dieses Tests lauten wie folgt:

Nullhypothese : Der Datensatz weist eine Schiefe und Kurtosis auf, die einer Normalverteilung entsprechen.

Alternativhypothese : Der Datensatz weist eine Schiefe und Kurtosis auf, die keiner Normalverteilung entsprechen .

Der folgende Code zeigt, wie dieser Test durchgeführt wird:

 jarque.test(data)

	Jarque-Bera Normality Test

data:data
JB = 5.7097, p-value = 0.05756
alternative hypothesis: greater

Der p-Wert des Tests beträgt 0,05756 . Da dieser Wert nicht kleiner als α = 0,05 ist, können wir die Nullhypothese nicht ablehnen. Wir haben keine ausreichenden Beweise dafür, dass dieser Datensatz eine von der Normalverteilung abweichende Schiefe und Kurtosis aufweist.

Die vollständige Dokumentation der Moments- Bibliothek finden Sie hier .

Bonus: Schiefe- und Kurtosis-Rechner

Sie können die Schiefe für einen bestimmten Datensatz auch mit dem Rechner für statistische Schiefe und Kurtosis berechnen , der automatisch Schiefe und Kurtosis für einen bestimmten Datensatz berechnet.