Bartletts test auf homogenität von varianzen (definition und beispiel)

Der Bartlett-Test ist ein statistischer Test, mit dem ermittelt wird, ob die Varianzen zwischen mehreren Gruppen gleich sind oder nicht.

Bei vielen statistischen Tests (z. B. einer einfaktoriellen ANOVA ) wird davon ausgegangen, dass die Varianzen zwischen den Stichproben gleich sind. Zur Überprüfung dieser Hypothese kann der Bartlett-Test verwendet werden.

In den folgenden Schritten wird die Durchführung des Bartlett-Tests erläutert.

Hinweis: Verwechseln Sie diesen Test nicht mit dem Bartlett-Test auf Sphärizität , der zum Vergleich einer beobachteten Korrelationsmatrix mit der Identitätsmatrix verwendet wird.

Schritte zur Durchführung des Bartlett-Tests

Der Bartlett-Test verwendet die folgenden Null- und Alternativhypothesen :

H ₀ : Die Varianz zwischen jeder Gruppe ist gleich.

H _A : Mindestens eine Gruppe weist eine Varianz auf, die nicht gleich der der anderen ist.

Die Teststatistik kann wie folgt berechnet werden:

B = (nk)lns ² – Σ(n _j -1)lns _j ² / c

Gold:

• n: die Gesamtzahl der Beobachtungen in allen Gruppen
• k: Die Gesamtzahl der Gruppen
• ln: Dies bedeutet „natürliches Protokoll“
• s ² : Die gepoolte Varianz
• nj: Die Anzahl der Beobachtungen in Gruppe _j
• s _j ² : Die Varianz der Gruppe j

Und wo es wie folgt berechnet wird:

• c = 1 + (1/3(k-1))*(Σ(1/(n _j -1)) – (1/(nk))

Diese Teststatistik folgt einer Chi-Quadrat-Verteilung mit k-1 Freiheitsgraden. Mit anderen Worten: B ~ X ² (k-1).

Wenn der p-Wert , der der Teststatistik entspricht, unter einem bestimmten Signifikanzniveau liegt (z. B. α = 0,05), können wir die Nullhypothese ablehnen und daraus schließen, dass nicht alle Gruppen die gleiche Varianz aufweisen.

Beispiel: Bartlett-Test

Angenommen, ein Professor möchte wissen, ob drei verschiedene Lerntechniken zu unterschiedlichen Durchschnittsnoten in Prüfungen führen.

Sie weist 10 Schülern nach dem Zufallsprinzip zu, jede Technik eine Woche lang anzuwenden, und gibt dann jedem Schüler eine Prüfung mit dem gleichen Schwierigkeitsgrad.

Nachfolgend werden die Prüfungsergebnisse der 30 Studierenden vorgestellt:

Die Professorin möchte eine einfaktorielle ANOVA durchführen, um zu sehen, ob die drei Techniken zu unterschiedlichen Durchschnittsergebnissen in der Prüfung führen. Sie muss jedoch zunächst den Bartlett-Test durchführen, um zu überprüfen, ob die drei Gruppen gleiche Varianzen aufweisen.

Da es mühsam ist, den Bartlett-Test manuell durchzuführen, geben wir die folgenden Datenwerte in den Bartlett-Testrechner ein:

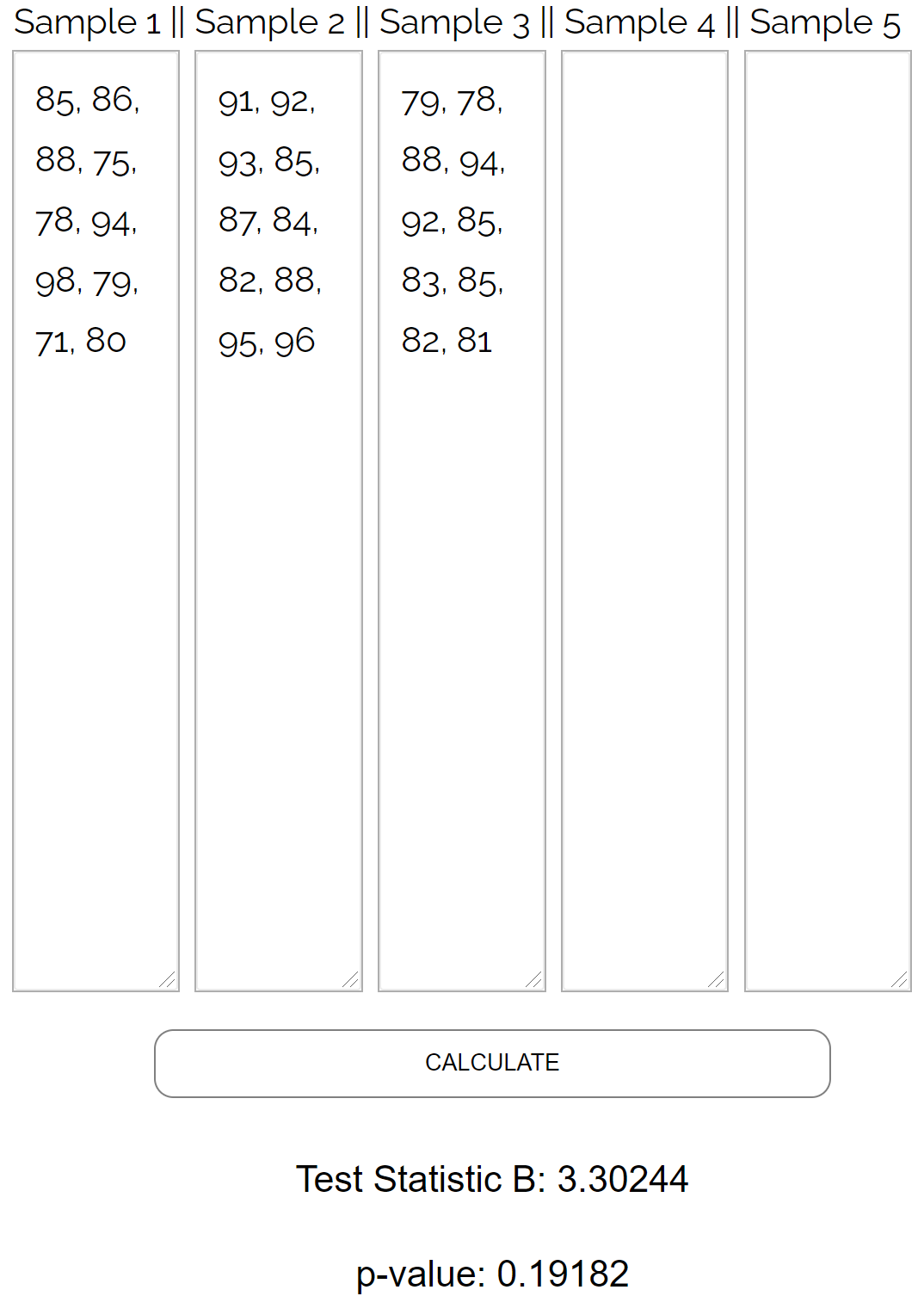
Der Test liefert folgende Ergebnisse:

• Teststatistik B : 3,30244
• P-Wert: 0,19182

Da der p-Wert nicht kleiner als 0,05 ist, wird der Professor die Nullhypothese nicht ablehnen. Mit anderen Worten: Sie verfügt nicht über ausreichende Beweise dafür, dass die drei Gruppen unterschiedliche Lücken aufweisen.

Somit kann sie mit der Durchführung der einfaktoriellen ANOVA fortfahren.

Zusätzliche Ressourcen

So führen Sie den Bartlett-Test in R durch (Schritt für Schritt)
So führen Sie den Bartlett-Test in Python durch (Schritt für Schritt)