Baum diagramm

In diesem Artikel wird erklärt, was ein Baumdiagramm ist und wie es erstellt wird. So finden Sie Beispiele für Baumstrukturen, die Vorteile dieses Diagrammtyps und zusätzlich eine Schritt für Schritt gelöste Übung.

Was ist ein Baum?

Ein Baumdiagramm , auch Wahrscheinlichkeitsbaum genannt, ist eine grafische Darstellung aller möglichen Ergebnisse eines Experiments zusammen mit ihren Wahrscheinlichkeiten.

Daher wird ein Baumdiagramm verwendet, um alle möglichen Ergebnisse in einem Stichprobenraum grafisch darzustellen und ihre Wahrscheinlichkeiten zu berechnen.

Ein Baumdiagramm wird so erstellt, dass jedes Ergebnis ( Knoten ) in neue mögliche Ergebnisse ( Zweige ) verzweigt, bis die Endergebnisse erreicht sind.

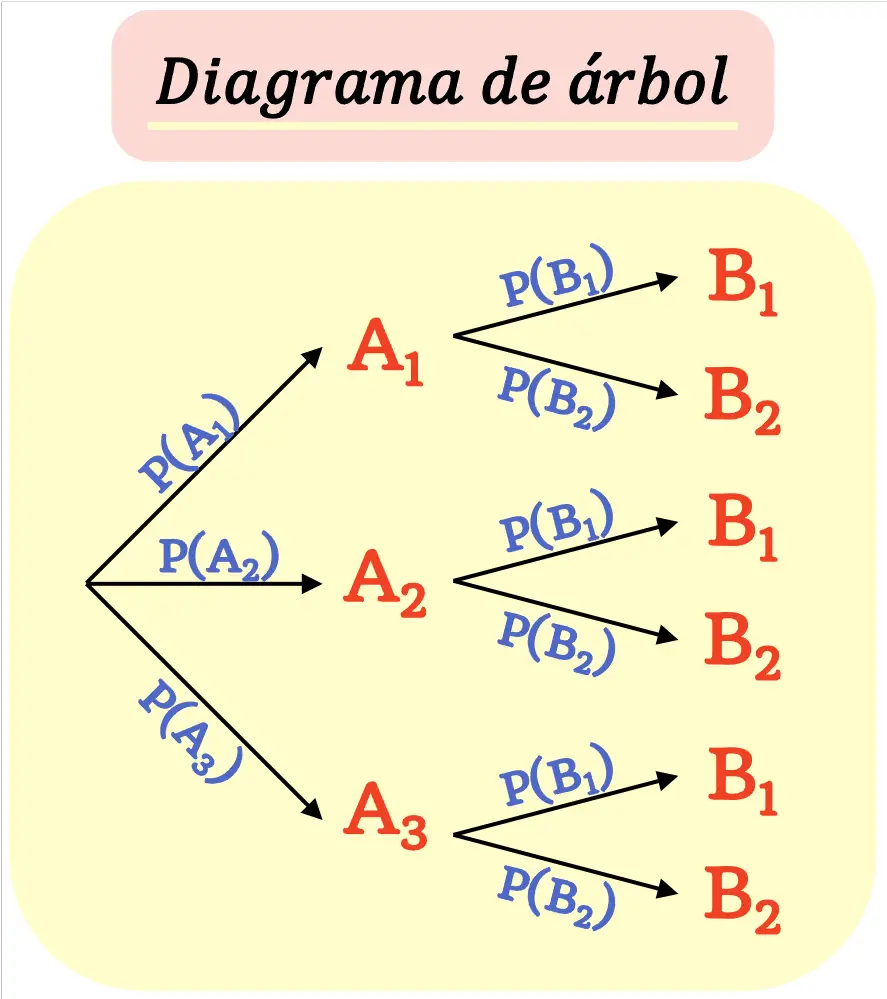
Es ist zu beachten, dass die Summe der Wahrscheinlichkeiten aller von einem Knoten ausgehenden Zweige gleich 1 sein muss.

So erstellen Sie ein Baumdiagramm

Um einen Baum zu erstellen, müssen Sie die folgenden Schritte ausführen:

1. Der erste Schritt beim Erstellen eines Baumdiagramms besteht darin, für jedes mögliche Ergebnis einen Zweig zu zeichnen. Dies werden die Filialen der ersten Generation sein.
2. Anschließend wird die mit jedem Ereignis verbundene Wahrscheinlichkeit zu seinem entsprechenden Zweig addiert.
3. Das Ende jedes Zweigs der ersten Generation ist ein Knoten, von dem aus Zweige nachfolgender möglicher Ereignisse dargestellt werden müssen.
4. Wie in den ersten Zweigen müssen wir die Wahrscheinlichkeiten der dargestellten Ereignisse addieren.
5. Wiederholen Sie die Schritte 3 und 4, bis Sie die letzten Knoten erreichen, also die möglichen Enden des Experiments.

Beachten Sie, dass die Anzahl der Zweige auf einer Ebene nicht unbedingt mit der Anzahl der Zweige auf einer anderen Ebene übereinstimmen muss. Ebenso kann die Anzahl der Verzweigungen, die sich aus einem möglichen Ergebnis ergeben, selbst innerhalb derselben Ebene variieren.

Baumbeispiel

Nachdem wir nun die Definition und Theorie zum Erstellen eines Baumdiagramms kennen, schauen wir uns Schritt für Schritt ein Beispiel aus der Praxis an, um das Konzept besser zu verstehen.

• Konstruieren Sie den Wahrscheinlichkeitsbaum für den Münzwurf von drei unabhängigen Münzen. Bestimmen Sie dann die Wahrscheinlichkeit, bei allen drei Würfen „Kopf“ zu bekommen.

Bei der Auslosung gibt es nur zwei mögliche Ergebnisse, wir können Kopf oder Zahl bekommen. Daher ist die Wahrscheinlichkeit, beim Münzwurf Kopf oder Zahl zu bekommen, wie folgt:

Sobald wir die Wahrscheinlichkeiten möglicher Ergebnisse kennen, fahren wir mit der Darstellung des Baumdiagramms fort.

Da Münzwürfe unabhängig voneinander erfolgen, ist die Wahrscheinlichkeit, Kopf oder Zahl zu erhalten, bei jedem Wurf immer gleich. Um den Baum zu bilden, müssen daher bei jedem Wurf zwei Zweige (Kopf und Zahl) mit der gleichen Wahrscheinlichkeit dargestellt werden.

Und sobald wir den Baum erstellt haben, müssen wir nur noch die Wahrscheinlichkeit bestimmen, mit der wir drei Münzen werfen.

Deshalb müssen wir in diesem Fall alle Wahrscheinlichkeiten, Kopf zu bekommen, multiplizieren, denn das sind die Wahrscheinlichkeiten des Weges, der uns zum gewünschten Ergebnis führt.

Somit wird die Wahrscheinlichkeit, bei den drei Münzwürfen „Kopf“ zu bekommen, wie folgt berechnet:

Kurz gesagt beträgt die Wahrscheinlichkeit, dreimal hintereinander Kopf zu bekommen, 12,5 %.

Baumübung gelöst

In einem Dorf gibt es nur 3 Kinderkrippen: 60 % der Kinder gehen in die Kinderkrippe A, 30 % in die Kinderkrippe B und 10 % in die Kinderkrippe C. Außerdem sind in den drei Kinderkrippen 55 % der Menschen Mädchen. Erstellen Sie den Baum und berechnen Sie die folgenden Wahrscheinlichkeiten:

• Wahrscheinlichkeit, dass es sich bei der zufälligen Auswahl eines Kindes um ein Mädchen aus der Kita B handelt.
• Wahrscheinlichkeit, dass es sich bei einem zufällig ausgewählten Kind aus einer Kindertagesstätte um einen Jungen handelt.

Beachten Sie, dass, wenn der Anteil der Mädchen in allen Kindertagesstätten 55 % beträgt, der Anteil der Jungen berechnet wird, indem einfach 1 minus 0,55 abgezogen wird:

Da wir nun alle Wahrscheinlichkeiten kennen, können wir den Wahrscheinlichkeitsbaum mit allen Möglichkeiten erstellen:

Somit errechnet sich die Wahrscheinlichkeit, zufällig ein Mädchen aus der Kita B auszuwählen, wie folgt:

Um andererseits die Wahrscheinlichkeit zu bestimmen, einen Jungen für eine Kindertagesstätte auszuwählen, müssen wir zunächst die Wahrscheinlichkeit ermitteln, für jede Kindertagesstätte einen Jungen auszuwählen, und diese dann addieren:

Vorteile der Baumstruktur

Aufgrund der Eigenschaften der Baumstruktur ergeben sich folgende Vorteile dieser Art von statistischem Diagramm:

• Baumdiagramme sind für die Entscheidungsfindung sehr hilfreich.
• Der Zusammenhang zwischen allen möglichen Ergebnissen kann grafisch dargestellt werden.
• Es ist sehr praktisch, die Grundursache eines Problems zu finden.
• Erleichtert die Lösung von Wahrscheinlichkeits- und Statistikproblemen.
• Ein Baumdiagramm hilft dabei, Ideen zu organisieren und die Situation zu analysieren.