So wenden sie den satz von bayes in excel an

Der Satz von Bayes besagt für zwei Ereignisse A und B Folgendes :

P(A|B) = P(A)*P(B|A) / P(B)

Gold:

• P(A|B): Die Wahrscheinlichkeit, dass Ereignis A bei gegebenem Ereignis B eingetreten ist.
• P(B|A): Die Wahrscheinlichkeit, dass Ereignis B unter der Voraussetzung, dass Ereignis A eingetreten ist, eingetreten ist.
• P(A): Die Wahrscheinlichkeit des Ereignisses A.
• P(B): Die Wahrscheinlichkeit des Ereignisses B.

Angenommen, die Wahrscheinlichkeit, dass das Wetter bewölkt ist, beträgt 40 %. Nehmen wir außerdem an, dass die Regenwahrscheinlichkeit an einem bestimmten Tag 20 % und die Wahrscheinlichkeit von Wolken an einem regnerischen Tag 85 % beträgt.

Wenn es an einem bestimmten Tag draußen bewölkt ist, wie hoch ist die Wahrscheinlichkeit, dass es an diesem Tag regnet?

Lösung :

• P(bewölkt) = 0,40
• P(Regen) = 0,20
• P(bewölkt | Regen) = 0,85

Somit können wir berechnen:

• P(Regen | bewölkt) = P(Regen) * P(bewölkt | Regen) / P(bewölkt)
• P(Regen | bewölkt) = 0,20 * 0,85 / 0,40
• P(Regen | bewölkt) = 0,425

Wenn es an einem bestimmten Tag draußen bewölkt ist, beträgt die Wahrscheinlichkeit, dass es an diesem Tag regnen wird, 0,425 oder 42,5 % .

Das folgende Beispiel zeigt, wie Sie genau dieses Problem mithilfe des Bayes-Theorems in Excel lösen können.

Beispiel: Bayes-Theorem in Excel

Die folgende Formel zeigt, wie der Satz von Bayes in Excel angewendet wird:

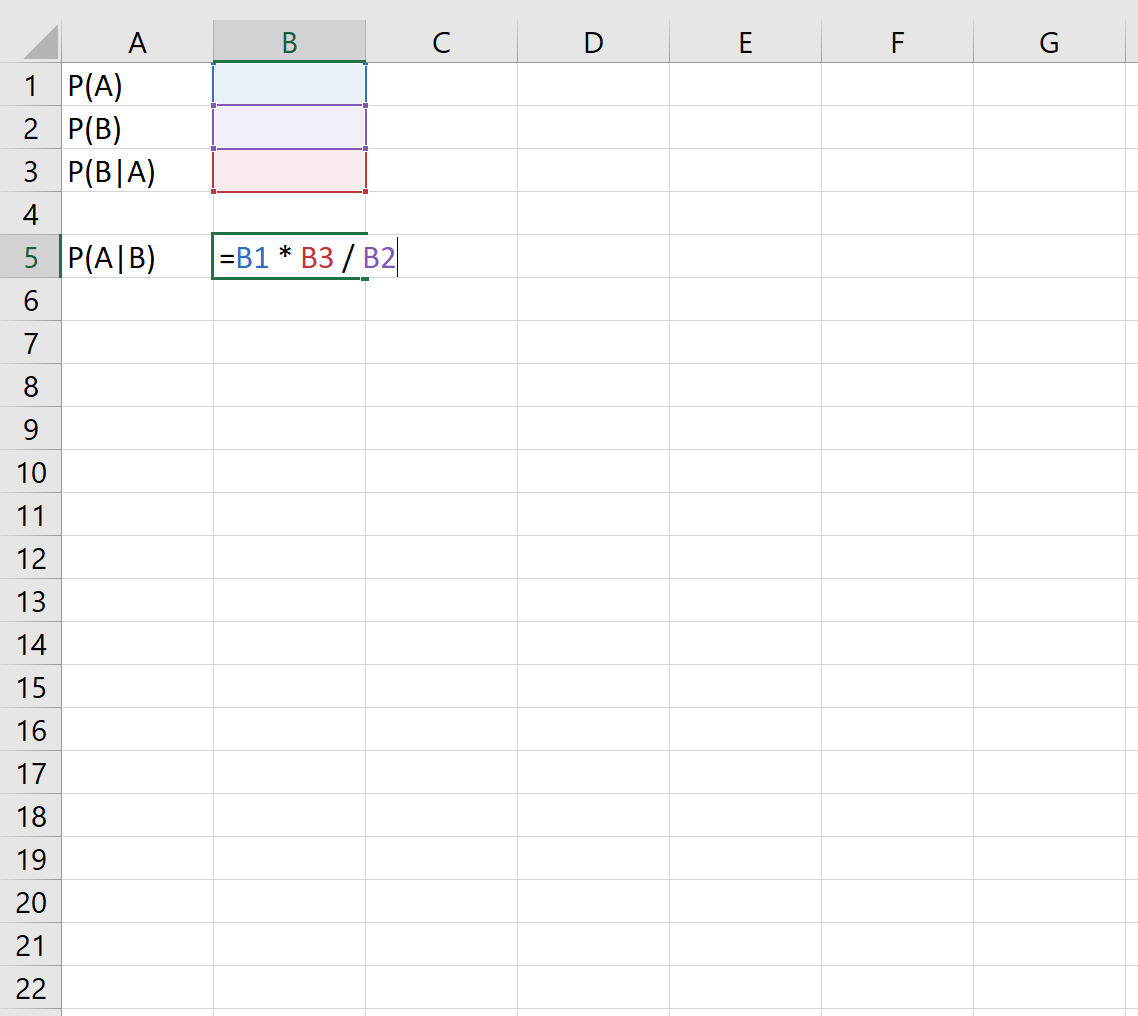
Wenn wir beispielsweise die folgenden Wahrscheinlichkeiten kennen:

• P(bewölkt) = 0,40
• P(Regen) = 0,20
• P(bewölkt | Regen) = 0,85

Dann können wir sie einfach in die Zellen von Excel einfügen:

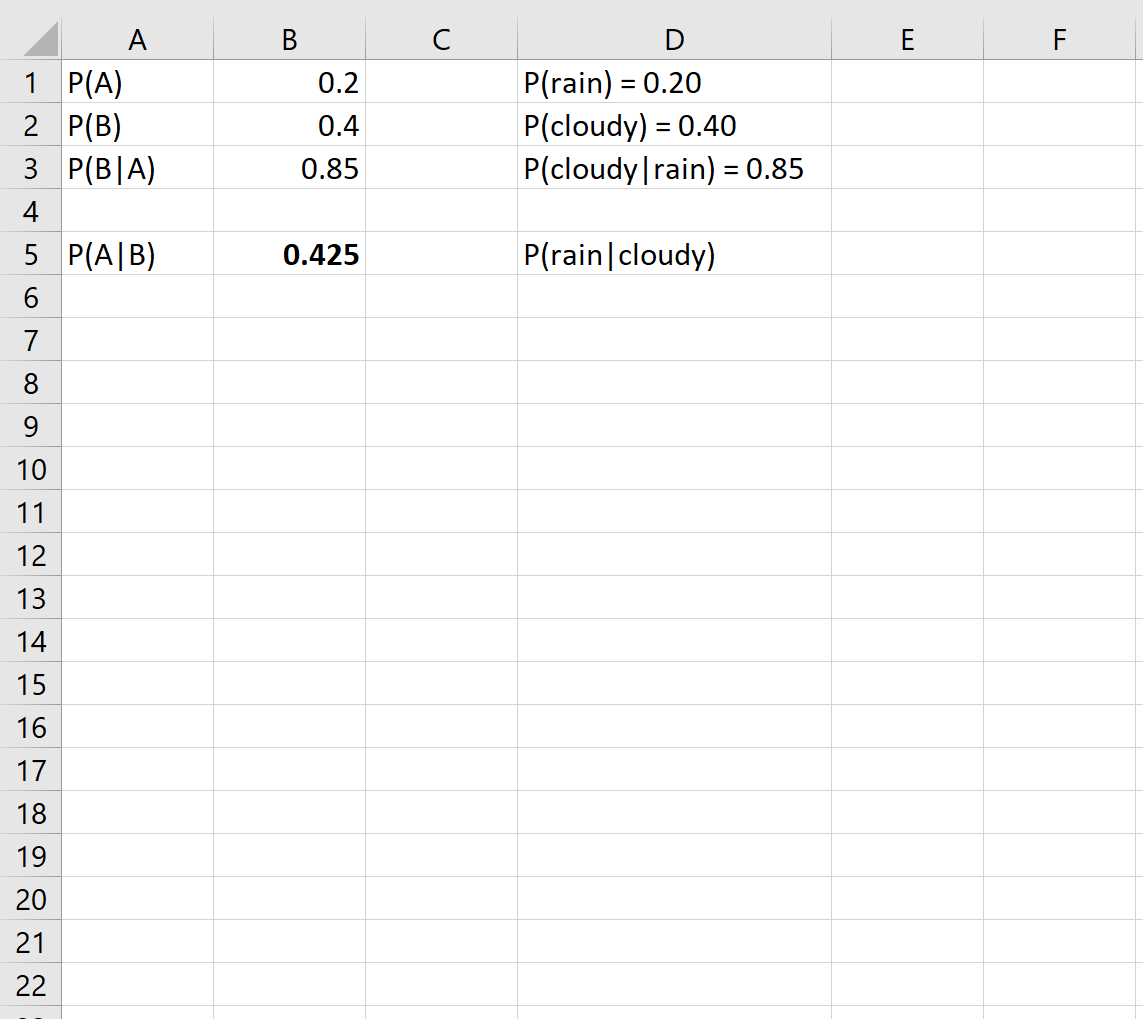
Dies sagt uns, dass die Wahrscheinlichkeit, dass es an diesem Tag regnet, 0,425 oder 42,5 % beträgt, wenn es an einem bestimmten Tag draußen bewölkt ist.

Zusätzliche Ressourcen

So berechnen Sie die bedingte Wahrscheinlichkeit in Excel
So wenden Sie die Faustregel in Excel an
So wenden Sie den zentralen Grenzwertsatz in Excel an