Die bedeutung der statistik im bildungswesen (mit beispielen)

Der Bereich Statistik beschäftigt sich mit der Erhebung, Analyse, Interpretation und Darstellung von Daten.

Im Bildungskontext sind Statistiken aus folgenden Gründen wichtig:

Grund 1 : Statistiken ermöglichen es Pädagogen, die Leistung von Schülern mithilfe deskriptiver Statistiken zu verstehen.

Grund 2 : Statistiken ermöglichen es Lehrern, mithilfe von Datenvisualisierungen Trends in der Schülerleistung zu erkennen.

Grund 3 : Statistiken ermöglichen es Pädagogen, verschiedene Lehrmethoden mithilfe von Hypothesentests zu vergleichen.

Im weiteren Verlauf dieses Artikels gehen wir auf jeden dieser Gründe ein.

Grund 1: Schülerleistungen mithilfe deskriptiver Statistiken verstehen

Beschreibende Statistiken werden zur Beschreibung von Daten verwendet.

Im pädagogischen Kontext kann ein Lehrer die folgenden deskriptiven Statistiken für die Schüler seiner Klasse berechnen:

• Die durchschnittliche Punktzahl bei einer bestimmten Prüfung.
• Die Standardabweichung der Ergebnisse einer bestimmten Prüfung.
• Der Bereich der Ergebnisse einer bestimmten Prüfung.
• Der Prozentsatz der Studierenden, die eine bestimmte Prüfung bestanden haben.
• Das 90. Perzentil der Ergebnisse einer bestimmten Prüfung.

Dank dieser Messungen kann der Lehrer die Ergebnisse der Schüler seiner Klasse bei einer bestimmten Prüfung besser verstehen.

Sie kann dann entscheiden, ob sie ihre Lehrmethode ändert, wenn zu wenige Studierende die Prüfung bestehen, oder ob sie möglicherweise zusätzliche Nachhilfemöglichkeiten für Studierende mit schlechten Prüfungsergebnissen usw. anbietet.

Hinweis : Diese Arten deskriptiver Statistiken werden auf allen Bildungsebenen verwendet. Ein Schulleiter kann beispielsweise deskriptive Statistiken verwenden, um die Testergebnisse der Schüler einer gesamten Schule zu überwachen. Ein staatliches Bildungsministerium kann auch deskriptive Statistiken verwenden, um die Testergebnisse von Schülern im gesamten Bundesstaat zu überwachen.

Grund 2: Trends mithilfe der Datenvisualisierung erkennen

Eine weitere gängige Methode zur Verwendung von Statistiken im Bildungswesen ist die Visualisierung von Daten wie Liniendiagrammen, Histogrammen, Boxplots, Kreisdiagrammen und anderen Diagrammen.

Diese Arten von Diagrammen werden häufig verwendet, um Pädagogen dabei zu helfen, Trends bei der Leistung im Klassenzimmer und bei der Leistung einzelner Schüler zu erkennen.

Angenommen, ein Lehrer erstellt das folgende Balkendiagramm, um die durchschnittliche Prüfungspunktzahl im Laufe des Jahres zu visualisieren:

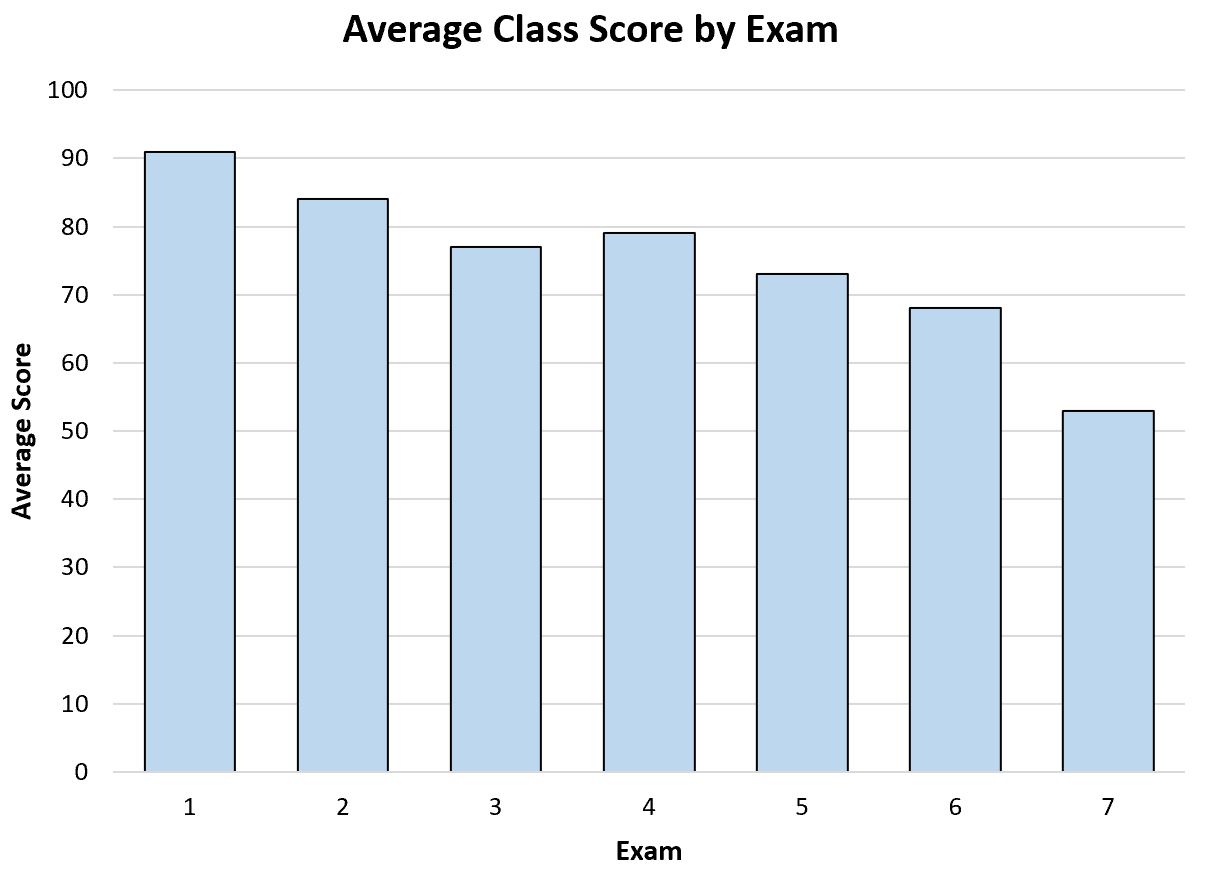
Anhand dieses Balkendiagramms kann der Lehrer erkennen, dass das durchschnittliche Testergebnis der Schüler seiner Klasse im Laufe des Jahres langsam abnimmt.

Dies kann es dem Lehrer ermöglichen, seine Lehrmethoden zu verbessern oder seinen Schülern eine Umfrage zu geben, um sie nach ihrer Meinung zu seinen Lehrmethoden usw. zu fragen.

Grund 3: Vergleichen Sie Lehrmethoden mithilfe von Hypothesentests

Statistiken werden auch in der Bildung in Form von Hypothesentests eingesetzt.

Hierbei handelt es sich um Tests, mit denen Pädagogen feststellen können, ob zwischen verschiedenen Lehrmethoden eine statistische Signifikanz besteht.

Angenommen, ein Lehrer möchte feststellen, ob sich ein bestimmter Lehrplan auf die Testergebnisse auswirkt. Um dies zu testen, wählt er nach dem Zufallsprinzip 15 Schüler aus, die einen Vortest absolvieren. Dann lässt er jeden Schüler einen Monat lang den Lehrplan anwenden und anschließend einen Nachtest mit ähnlichem Schwierigkeitsgrad absolvieren.

Die Testergebnisse für jeden der 15 Studenten sind unten aufgeführt:

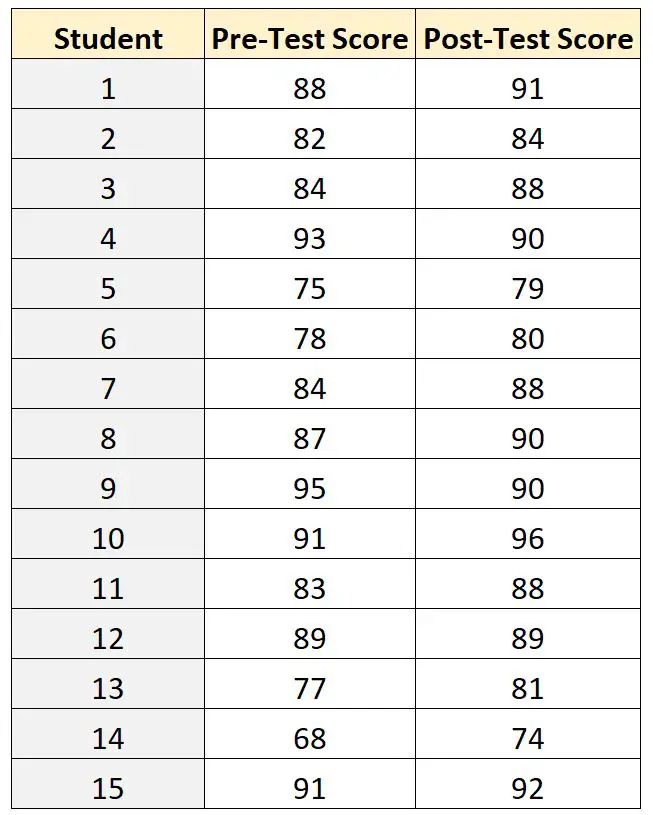
Um die Differenz zwischen den Durchschnittswerten vor und nach dem Test zu vergleichen, kann der Lehrer gepaarte T-Test-Stichproben verwenden, da für jeden Schüler die Punktzahl vor dem Test mit der Punktzahl nach dem Test verknüpft werden kann.

Angenommen, der Professor verwendet Statistiksoftware, um diesen T-Test bei gepaarten Stichproben durchzuführen, und erhält die folgenden Ergebnisse:

• T-Test-Statistik: -2,97
• p-Wert: 0,0101

In diesem Beispiel verwendet der T-Test für gepaarte Stichproben die folgenden Null- und Alternativhypothesen:

• H ₀ : Die durchschnittlichen Ergebnisse vor und nach dem Test sind gleich
• H _A : Die durchschnittlichen Ergebnisse vor und nach dem Test sind nicht gleich

Da der p-Wert ( 0,0101 ) kleiner als 0,05 ist, lehnen wir die Nullhypothese ab.

Das heißt, wir haben genügend Belege dafür, dass das durchschnittliche Testergebnis für Studierende vor und nach der Teilnahme am Studienprogramm unterschiedlich ist.

Hinweis : Dies ist nur ein Beispiel für Hypothesentests, die in der Bildung eingesetzt werden. Andere gängige Tests sind ein T-Test bei einer Stichprobe , ein T-Test bei zwei Stichproben , eine einfaktorielle ANOVA und eine zweifaktorielle ANOVA .

Zusätzliche Ressourcen

Die folgenden Artikel erläutern die Bedeutung von Statistiken in anderen Bereichen:

Die Bedeutung von Statistiken in Unternehmen
Die Bedeutung der Statistik in der Wirtschaft
Die Bedeutung von Statistiken im Gesundheitswesen