Warum ist der median in der statistik wichtig?

Der Median stellt den Mittelwert eines Datensatzes dar, wenn alle Werte vom kleinsten zum größten geordnet sind.

Der Median im folgenden Datensatz beträgt beispielsweise 19:

Datensatz: 3, 4, 11, 15, 19 , 22, 23, 23, 26

Der Median repräsentiert auch das ^50. Perzentil eines Datensatzes. Das heißt, genau die Hälfte der Werte im Datensatz liegt über dem Median und die Hälfte der Werte liegt darunter.

Der Median ist eine wichtige zu berechnende Metrik, da er uns eine Vorstellung davon gibt, wo sich das „Zentrum“ eines Datensatzes befindet. Dies gibt uns auch eine Vorstellung vom „typischen“ Wert in einem bestimmten Datensatz.

Nehmen wir zum Beispiel an, wir haben einen Datensatz, der die Verkaufspreise von 10.000 verschiedenen Häusern in einer bestimmten Stadt enthält.

Anstatt zeilenweise Rohdaten zu betrachten, können wir den Medianwert berechnen, um schnell den durchschnittlichen Verkaufspreis von Häusern in dieser Stadt zu ermitteln.

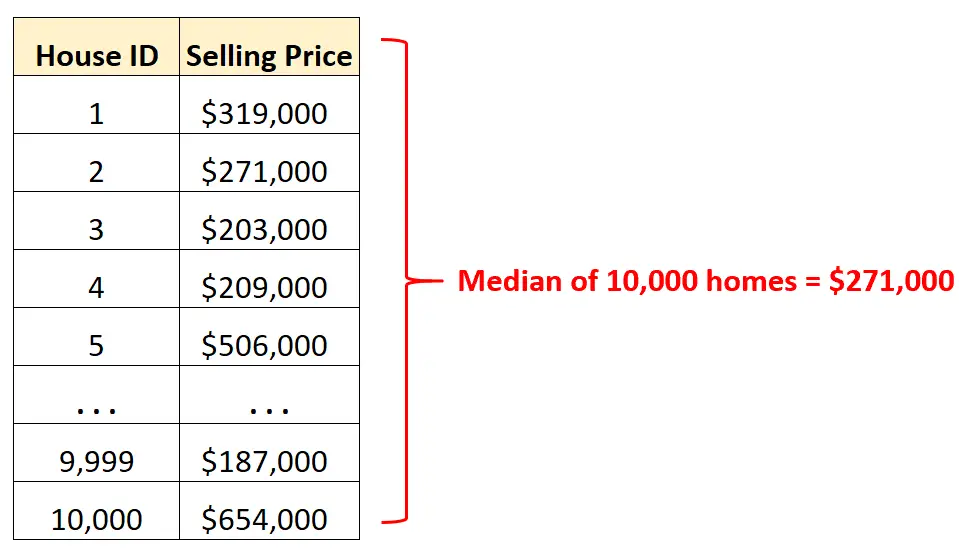
Da wir wissen, dass der durchschnittliche Verkaufspreis 271.000 US-Dollar beträgt, wissen wir, dass genau die Hälfte der 10.000 Häuser für mehr als diesen Betrag und die andere Hälfte für weniger verkauft wurde.

Dies gibt uns auch eine Vorstellung vom „typischen“ Verkaufspreis von Häusern in dieser Stadt.

Wann ist der Median zu verwenden?

Bei der Analyse von Datensätzen wollen wir oft verstehen, wo der zentrale Wert liegt.

In der Statistik gibt es zwei gängige Metriken, mit denen wir den Mittelpunkt eines Datensatzes messen:

• Mittelwert : der Durchschnittswert in einem Datensatz
• Median : Der Medianwert in einem Datensatz

Es stellt sich heraus, dass der Median unter folgenden Umständen ein nützlicheres Maß ist:

• Wenn die Verteilung asymmetrisch ist.
• Wenn die Verteilung Ausreißer enthält.

Um dies zu veranschaulichen, betrachten Sie die folgenden zwei Beispiele.

Beispiel 1: Berechnung des Medians einer schiefen Verteilung

Betrachten Sie die folgende Gehaltsverteilung für Einwohner einer bestimmten Stadt:

Der Median spiegelt das „typische“ Gehalt eines Bewohners besser wider als der Durchschnitt, da die Verteilung rechtsschief ist.

Das bedeutet, dass hohe Löhne auf der rechten Seite der Verteilung den Mittelwert aus der Mitte der Verteilung verschieben.

In diesem speziellen Beispiel beträgt das Durchschnittsgehalt 47.000 US-Dollar, während das Durchschnittsgehalt 32.000 US-Dollar beträgt. Der Median ist viel repräsentativer für das typische Gehalt in dieser Stadt.

Beispiel 2: Berechnung des Medians bei Vorhandensein von Ausreißern

Betrachten Sie die folgende Grafik, die die Quadratmeterzahl von Häusern in einer bestimmten Straße zeigt:

Der Durchschnitt wird stark von einigen wenigen extrem großen Häusern beeinflusst, während dies beim Median nicht der Fall ist.

Wir können sehen, dass der Median die „typische“ Quadratmeterzahl eines Hauses in dieser Straße besser erfasst als der Durchschnitt, da er nicht durch Ausreißer beeinflusst wird.

Zusammenfassung

Hier ist eine kurze Zusammenfassung der wichtigsten Punkte, die in diesem Artikel behandelt werden:

• Der Median stellt den Mittelwert in einem Datensatz dar.
• Der Median ist wichtig, weil er uns eine Vorstellung davon gibt, wo der zentrale Wert in einem Datensatz liegt.
• Der Median ist tendenziell nützlicher zu berechnen als der Mittelwert, wenn eine Verteilung schief ist und/oder Ausreißer aufweist.

Zusätzliche Ressourcen

Konkrete Beispiele: Verwendung von Mittelwert, Median und Modus
Wann sollte der Mittelwert vs. verwendet werden? Median: Mit Beispielen
Warum ist der Modus in der Statistik wichtig?