Warum ist der modus in der statistik wichtig?

Der Modus stellt den Wert dar, der in einem Datensatz am häufigsten vorkommt.

Ein Datensatz kann keinen Modus (wenn sich keine Werte wiederholen), einen Modus oder mehrere Modi haben.

Der Modus im folgenden Datensatz ist beispielsweise 19:

Datensatz: 3, 4, 11, 15, 19 , 19, 19 , 22 , 22, 23, 23, 26

Dies ist der Wert, der am häufigsten vorkommt.

In der Statistik ist der Modus aus folgenden Gründen wichtig:

Grund 1 : Dadurch wissen wir, welche Werte in einem Datensatz am häufigsten vorkommen.

Grund 2 : Es ist nützlich, den häufigsten Wert in kategorialen Daten zu finden, wenn der Mittelwert und der Median nicht berechnet werden können.

Grund 3 : Es gibt uns eine Vorstellung davon, wo sich das „Zentrum“ eines Datensatzes befindet, auch wenn Median und Mittelwert häufiger verwendet werden (wie wir später in diesem Artikel sehen werden).

Die folgenden Beispiele veranschaulichen jeden dieser Gründe in der Praxis.

Grund 1: Der Modus sagt uns, welcher Wert am häufigsten vorkommt

Nehmen wir an, wir haben einen Datensatz mit 100.000 Zeilen, der die Verkaufspreise von Häusern in den Vereinigten Staaten enthält:

Angenommen, wir verwenden Statistiksoftware (wie Excel , R , Python usw.), um den Modus dieses Datensatzes zu berechnen, und stellen fest, dass es drei Modi gibt:

• 280.000 $
• 300.000 $
• 305.000 US-Dollar

Dies gibt uns sofort eine Vorstellung von den häufigsten Immobilienpreisen im Datensatz.

Die Berechnung der Mode-Tausender ist auch viel schneller als die Betrachtung von Datenzeilen und der Versuch herauszufinden, welche Hauspreise am häufigsten vorkommen.

Grund 2: Der Modus sucht nach dem häufigsten Wert in kategorialen Daten

Angenommen, wir haben einen Datensatz mit 1.000 Zeilen, der uns die Farbe des Autos verrät, das Einzelpersonen in einer bestimmten Nachbarschaft gehört:

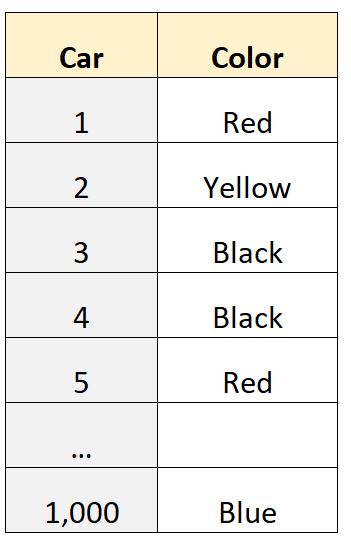
Die Variable „Farbe“ ist eine kategoriale Variable , was bedeutet, dass die Werte zu Kategorien („rot“, „gelb“, „schwarz“ usw.) gehören und wir daher keinen quantitativen Wert wie den Durchschnitt oder den Median berechnen können .

Wir können den Modus jedoch berechnen, da er einfach den häufigsten Wert im Datensatz darstellt.

Beispielsweise könnten wir mithilfe einer Statistiksoftware feststellen, dass der Modus dieses Datensatzes „Schwarz“ ist, was uns sagt, dass die häufigste Autofarbe in diesem Datensatz Schwarz ist.

Grund 3: Der Modus gibt uns eine Vorstellung davon, wo sich das Zentrum eines Datensatzes befindet

Der Modus gilt auch als Maß für die zentrale Tendenz , was bedeutet, dass er uns eine Vorstellung davon geben kann, wo sich das „Zentrum“ des Datensatzes befindet.

Angenommen, wir haben den folgenden Datensatz, der die Prüfungsergebnisse von 20 verschiedenen Schülern einer Klasse zeigt:

Der Modus liegt bei 82 – das ist die häufigste Prüfungspunktzahl. Dies erweist sich auch als guter Hinweis darauf, wo der „Kernwert“ der Bewertungspunktzahl in diesem Datensatz liegt.

Nehmen wir jedoch an, wir hätten stattdessen den folgenden Datensatz mit Prüfungsergebnissen:

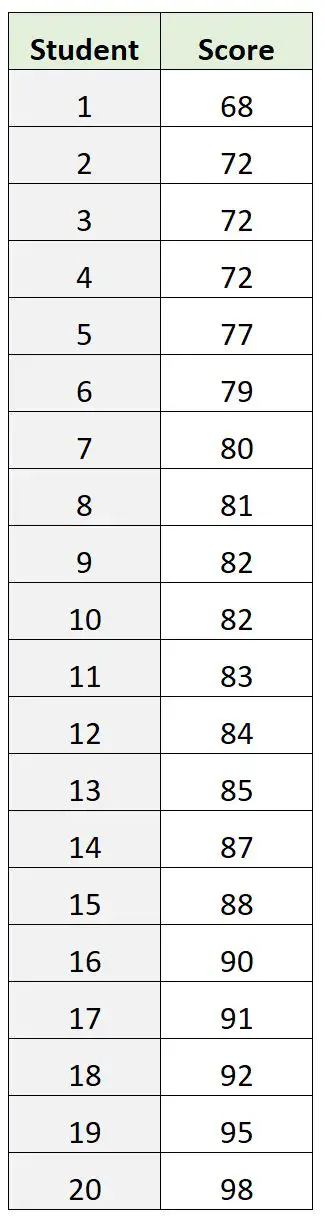
In diesem Datensatz ist 72 die Punktzahl der Modeprüfung. Dies erweist sich jedoch als schlechter Hinweis darauf, wo die „Kern“-Punktzahl der Prüfung liegt.

Die durchschnittliche Prüfungspunktzahl liegt bei 82,9 und die mittlere Prüfungspunktzahl bei 82,5 , was uns beide eine bessere Vorstellung davon gibt, wo der „zentrale“ Wert in Bezug auf die Mode liegt.

Zusammenfassung

Hier ist eine kurze Zusammenfassung der wichtigsten Punkte, die in diesem Artikel behandelt werden:

• Der Modus stellt die Werte dar, die in einem Datensatz am häufigsten vorkommen.
• Der Modus gibt uns den häufigsten Wert in kategorialen Daten an, wenn der Mittelwert und der Median nicht verwendet werden können.
• Der Modus gibt uns eine Vorstellung davon, wo sich das „Zentrum“ eines Datensatzes befindet, kann jedoch im Vergleich zum Mittelwert oder Median irreführend sein.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zu Mittelwert, Median und Modus in der Statistik:

Warum ist der Durchschnitt in der Statistik wichtig?
Warum ist der Median in der Statistik wichtig?
Konkrete Beispiele: Verwendung von Mittelwert, Median und Modus
Wann sollte der Mittelwert vs. verwendet werden? Median: Mit Beispielen