5 beispiele für nichtlineare beziehungen zwischen variablen

In den meisten Statistikkursen lernen die Studierenden lineare Beziehungen zwischen Variablen kennen.

Hierbei handelt es sich um Beziehungen, bei denen ein Anstieg einer Variablen mit einem vorhersehbaren Anstieg einer anderen Variablen verbunden ist.

Ein Beispiel hierfür könnte die Anzahl der gespielten Minuten eines Basketballspiels im Vergleich zur Gesamtpunktzahl sein:

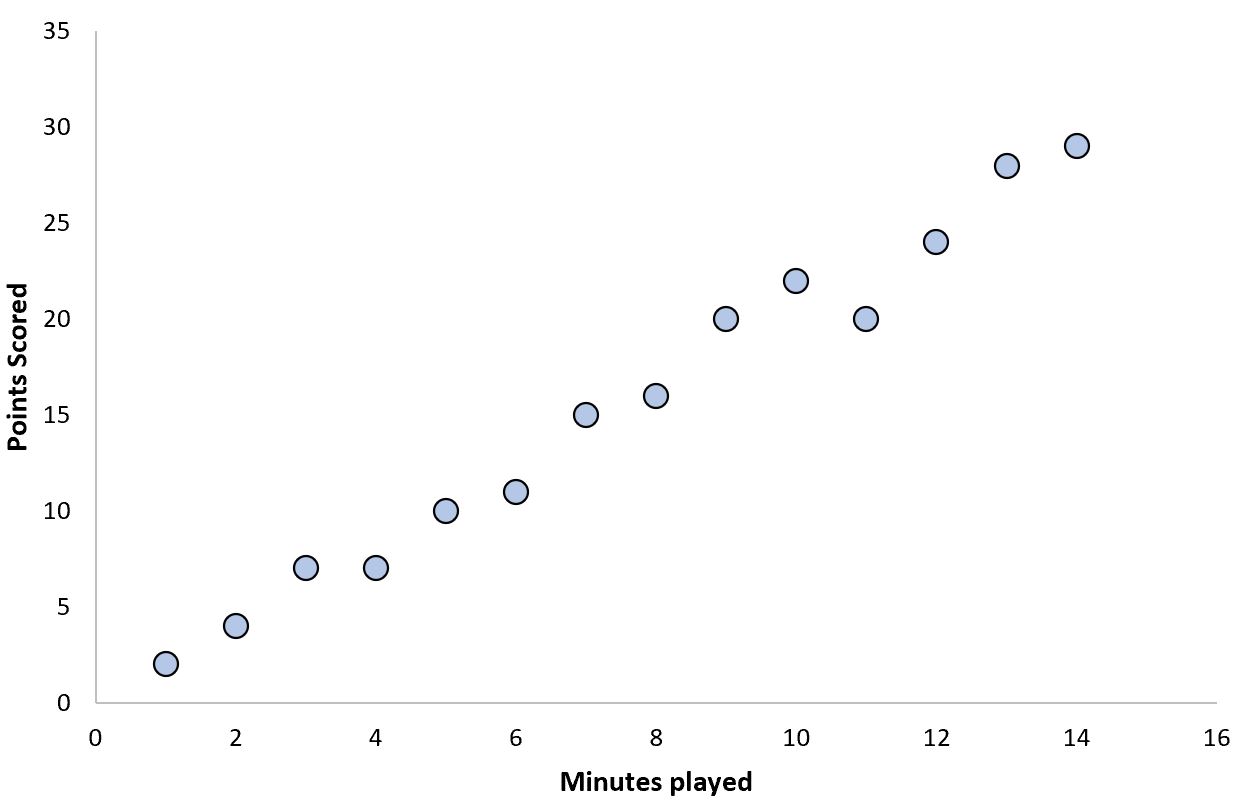
Spieler, die mehr Minuten spielen, erzielen tendenziell mehr Punkte.

Allerdings kann es auch nichtlineare Zusammenhänge zwischen Variablen geben und diese treten in der realen Welt ständig auf.

Dieses Tutorial bietet fünf Beispiele für nichtlineare Beziehungen zwischen Variablen in der realen Welt.

Beispiel 1: Quadratische Beziehungen

Eine der häufigsten nichtlinearen Beziehungen in der realen Welt ist die quadratische Beziehung zwischen Variablen.

Bei der Darstellung in einem Streudiagramm hat diese Beziehung typischerweise eine „U“-Form.

Ein Beispiel könnte die Gesamtarbeitszeit pro Woche im Vergleich zur Gesamtzufriedenheit sein:

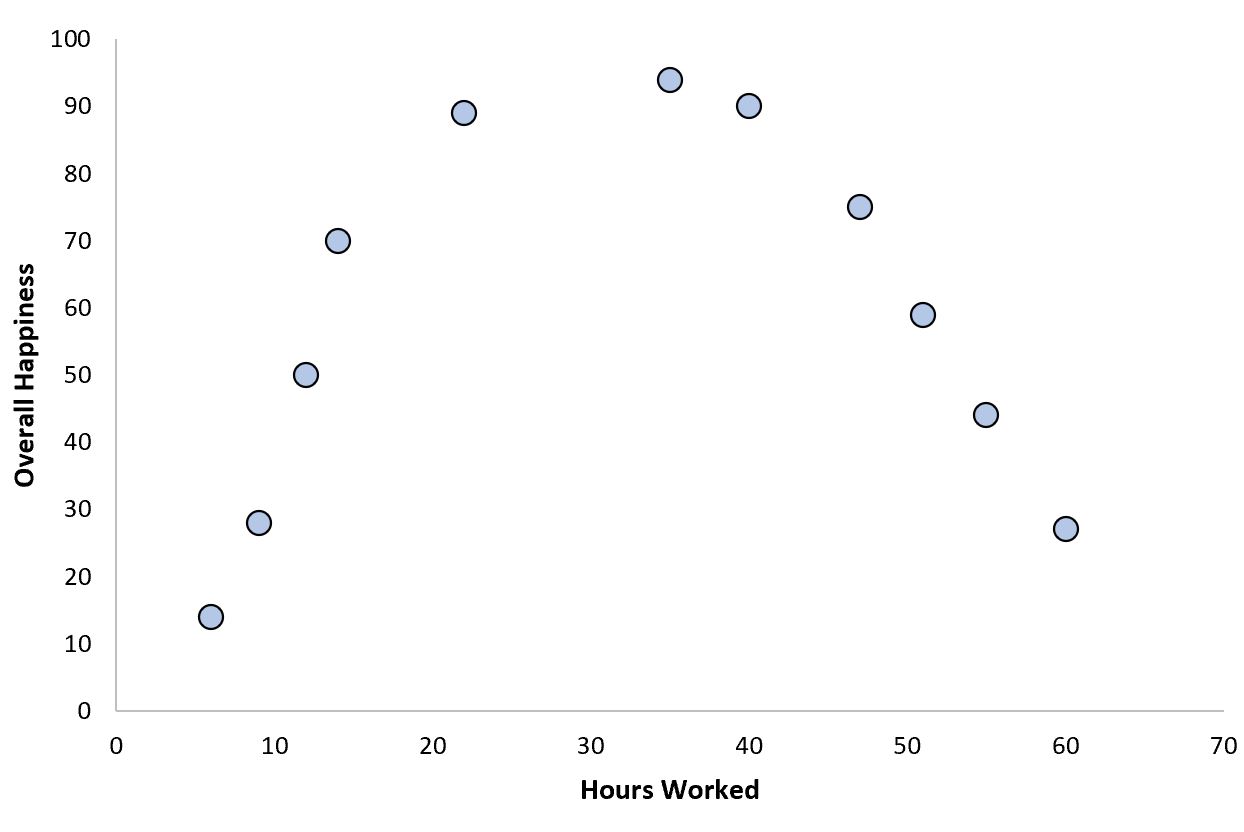
Wenn die Arbeitsstunden von Null an ansteigen, nimmt die allgemeine Zufriedenheit tendenziell zu, aber ab einem bestimmten Schwellenwert führen mehr Arbeitsstunden tatsächlich zu einem Rückgang der Zufriedenheit.

Diese umgekehrte „U“-Form ist die charakteristische Form einer quadratischen Beziehung zwischen zwei Variablen.

Beispiel 2: Kubische Beziehungen

Eine weitere nichtlineare Beziehung, die in der realen Welt häufig vorkommt, ist die kubische Beziehung zwischen Variablen.

Bei der Darstellung in einem Streudiagramm zeigt diese Beziehung typischerweise zwei unterschiedliche Kurven.

Diese Art von Beziehung besteht häufig zwischen Variablen im Bereich der Thermodynamik:

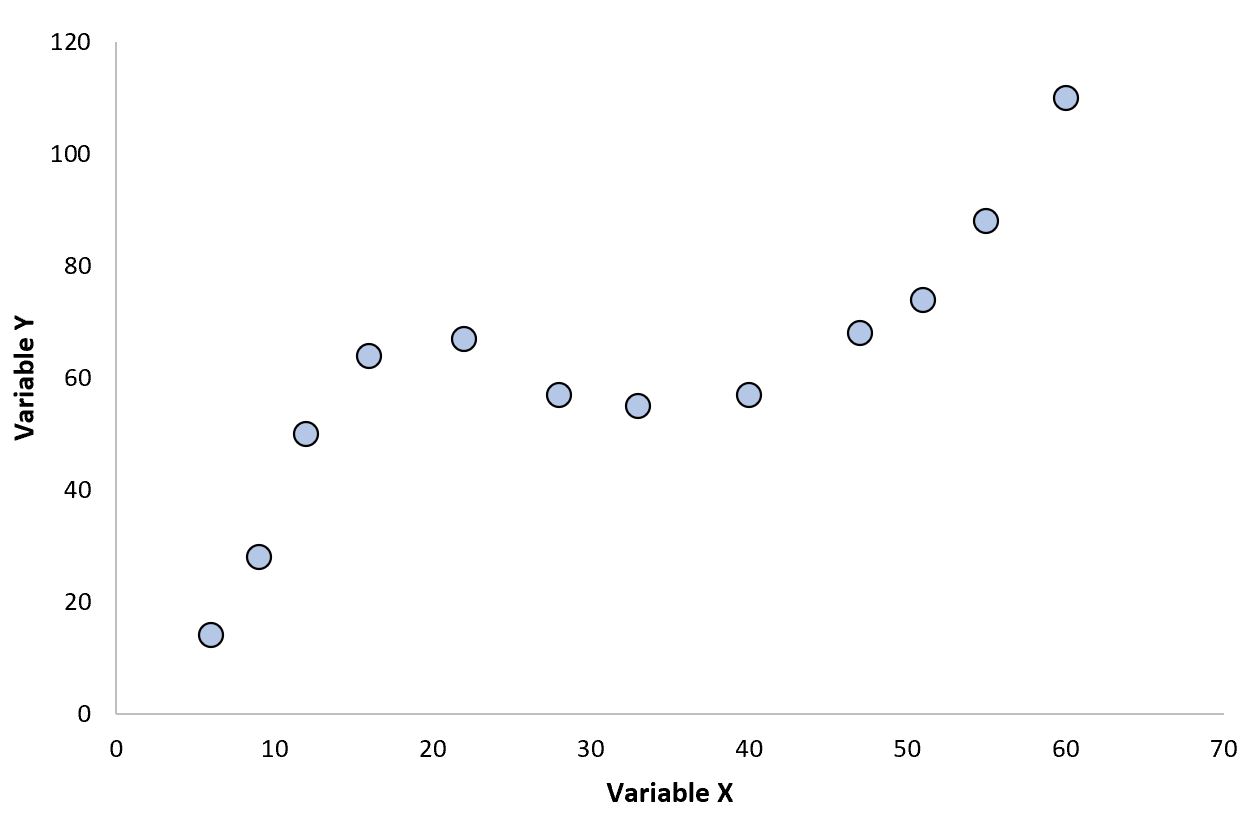
Beachten Sie, dass es im Diagramm zwei unterschiedliche Kurven gibt und dass die Beziehung zwischen Variable X und Variable Y eindeutig nicht linear ist.

Beispiel 3: Exponentielle Beziehungen

Eine weitere nichtlineare Beziehung, die in der realen Welt häufig vorkommt, ist die exponentielle Beziehung zwischen Variablen.

Bei der Darstellung in einem Streudiagramm zeigt diese Beziehung eine einzigartige Kurve, die mit zunehmender Variable auf der x-Achse ausgeprägter wird.

Ein bekanntes Beispiel für einen exponentiellen Zusammenhang ist die Lebensdauer von Bambuspflanzen und ihr jährliches Wachstum:

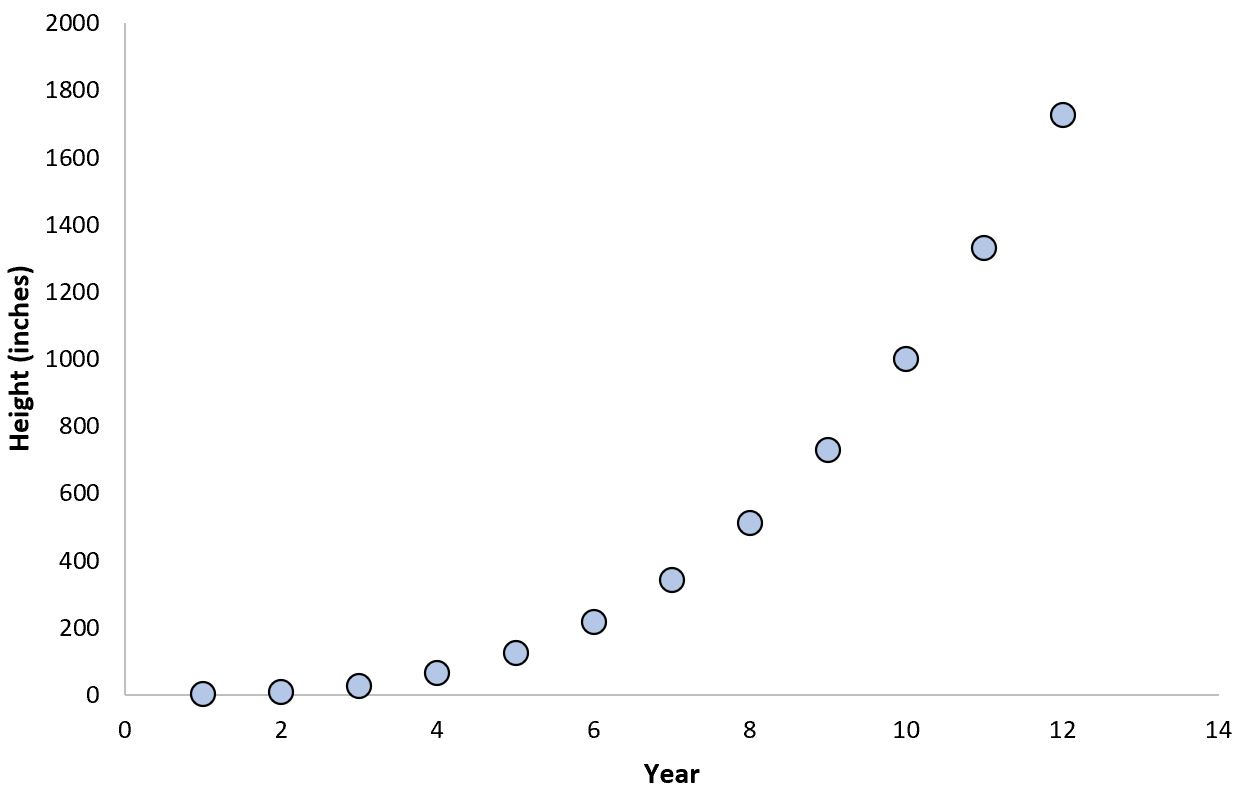
In den ersten Wachstumsjahren wächst eine Bambuspflanze sehr langsam, aber sobald sie ein bestimmtes Alter erreicht, explodiert sie in der Höhe und wächst rasant.

Beispiel 4: Logarithmische Beziehungen

Eine weitere nichtlineare Beziehung, die in der realen Welt häufig vorkommt, ist die logarithmische Beziehung zwischen Variablen.

Bei der Darstellung in einem Streudiagramm zeigt diese Beziehung eine einzigartige Kurve, die mit zunehmender Variable auf der x-Achse weniger ausgeprägt wird.

Ein Beispiel für einen logarithmischen Zusammenhang ist der zwischen der Effizienz von Smart-Home-Technologien und der Zeit:

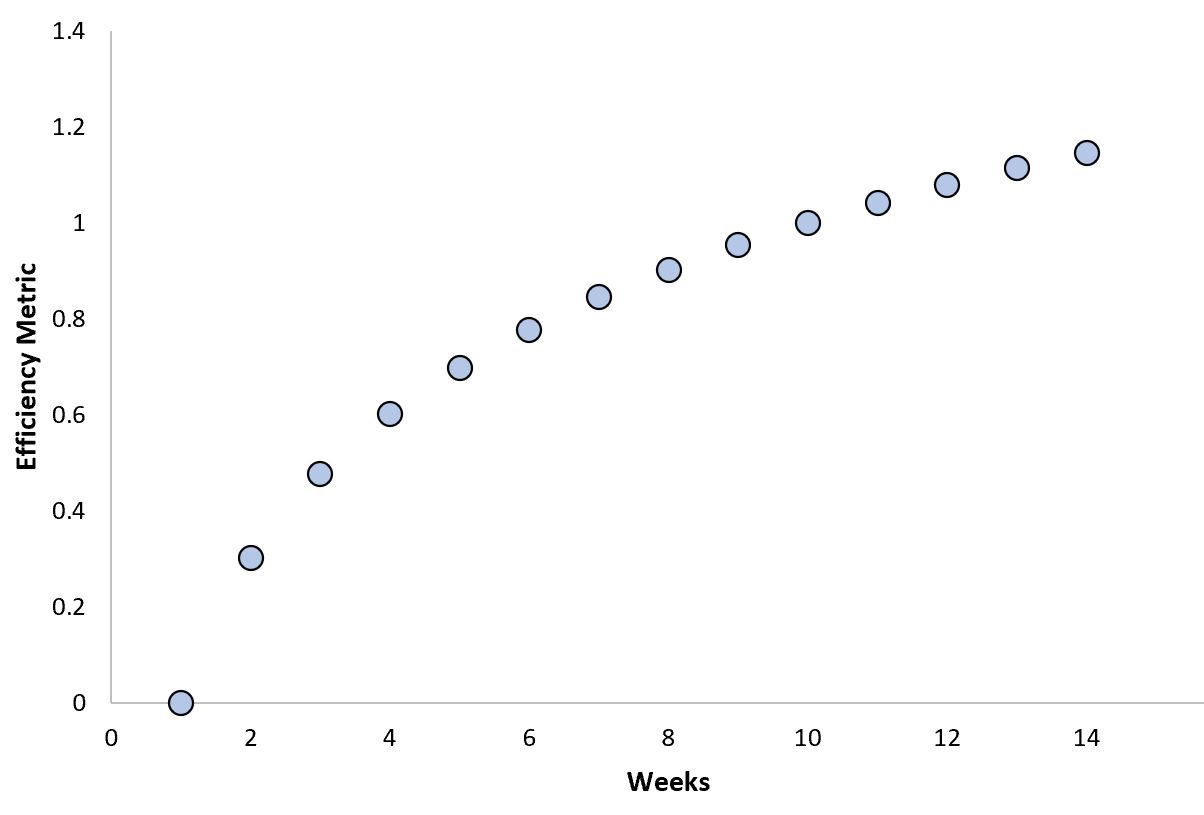
Wenn neue Smart-Home-Technologie (wie ein Staubsauger oder eine eigenständige Klimaanlage) in einem Haus installiert wird, lernt sie schnell, effizienter zu werden, aber sobald sie einen bestimmten Punkt erreicht, erreicht sie eine maximale Effizienzschwelle.

Beispiel 5: Kosinusbeziehungen

Eine weitere nichtlineare Beziehung, die in der realen Welt häufig vorkommt, ist die Kosinusbeziehung zwischen Variablen.

Bei der Darstellung in einem Streudiagramm hat diese Beziehung eine „Wellenform“.

Ein Beispiel für eine Kosinusbeziehung ist die zwischen der Frequenz von Schallwellen und der Zeit:

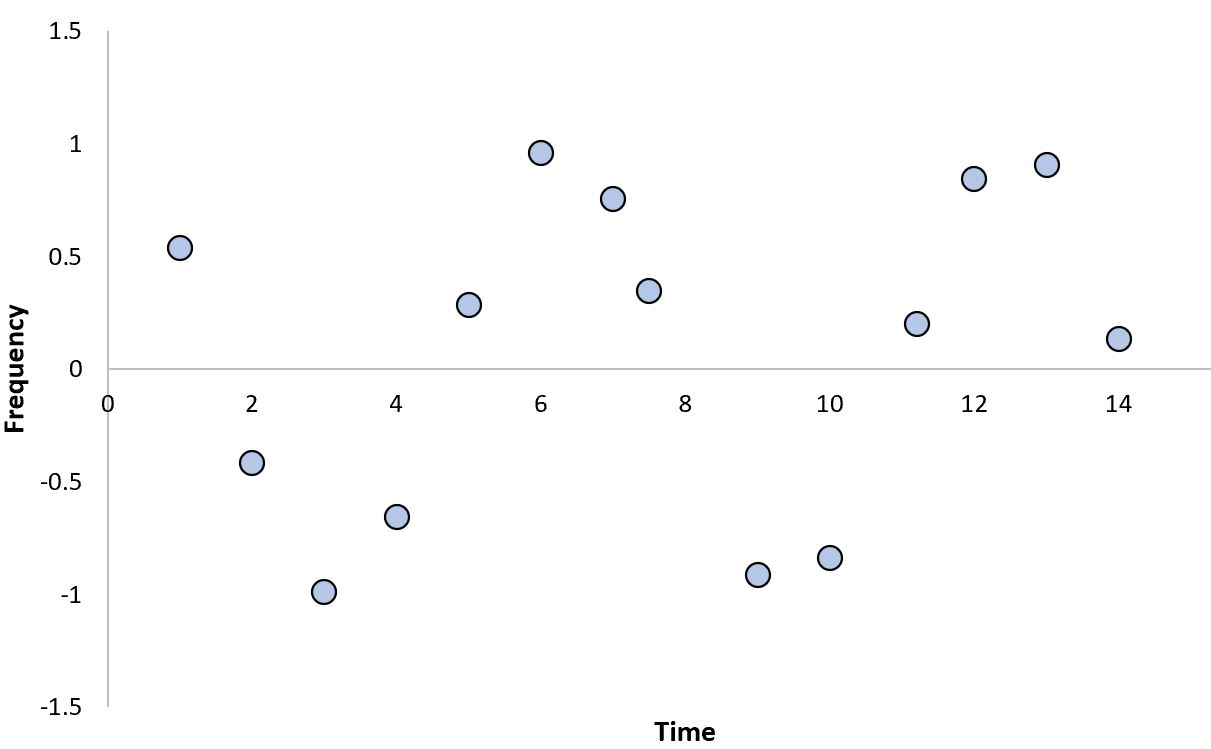
Beachten Sie, dass die Beziehung eine „Wellenform“ hat, die stark nichtlinear ist.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie verschiedene Arten der nichtlinearen Regression in Excel durchführen:

So führen Sie eine quadratische Regression in Excel durch
So führen Sie eine kubische Regression in Excel durch
So führen Sie eine exponentielle Regression in Excel durch
So führen Sie eine logarithmische Regression in Excel durch