Ein leitfaden zum benjamini-hochberg-verfahren

Jedes Mal, wenn Sie einen statistischen Test durchführen, ist es möglich, dass Sie rein zufällig einen p-Wert von weniger als 0,05 erhalten, selbst wenn Ihre Nullhypothese wahr ist.

Angenommen, Sie möchten wissen, ob eine bestimmte Pflanze eine durchschnittliche Höhe von mehr als 10 Zoll hat. Ihre Null- und Alternativhypothesen zum Testen wären:

H ₀ : μ = 10 Zoll

_HA : μ > 10 Zoll

Um diese Hypothese zu testen, können Sie eine Zufallsstichprobe von 20 Pflanzen zur Messung sammeln. Auch wenn die wahre Durchschnittshöhe dieser Pflanzenart 10 Zoll beträgt, ist es möglich, dass Sie eine Stichprobe von 20 ungewöhnlich hohen Pflanzen ausgewählt haben, was Sie dazu veranlasst, die Nullhypothese abzulehnen.

Selbst wenn die Nullhypothese wahr wäre (die durchschnittliche Höhe dieser Pflanze betrug tatsächlich 10 Zoll), haben Sie sie abgelehnt. In der Statistik nennen wir dies eine „falsche Entdeckung“. Sie behaupten, eine Entdeckung gemacht zu haben – ein „signifikantes Ergebnis“ –, aber das ist tatsächlich falsch.

Stellen Sie sich nun vor, Sie würden 100 statistische Tests gleichzeitig durchführen. Bei einem Alpha-Wert von 0,05 beträgt die Wahrscheinlichkeit, dass bei einem einzelnen Test eine falsche Entdeckung gemacht wird, nur 5 %. Da Sie jedoch eine so große Anzahl von Tests durchführen, würden Sie davon ausgehen, dass nur etwa 5 von 100 zu falschen Entdeckungen führen.

In der modernen Welt können falsche Entdeckungen ein häufiges Problem sein, da die Technologie es Forschern ermöglicht hat, Hunderte oder sogar Tausende statistischer Tests gleichzeitig durchzuführen.

Beispielsweise können medizinische Forscher statistische Tests an Zehntausenden Genen gleichzeitig durchführen. Selbst bei einer Falscherkennungsrate von nur 5 % bedeutet das, dass Hunderte von Tests zu falschen Entdeckungen führen könnten.

Eine Möglichkeit, die Falscherkennungsrate zu kontrollieren, ist die Verwendung des sogenannten Benjamini-Hochberg-Verfahrens.

Das Benjamini-Hochberg-Verfahren

Das Benjamini-Hochberg-Verfahren funktioniert wie folgt:

Schritt 1: Führen Sie alle Ihre statistischen Tests durch und ermitteln Sie den p-Wert für jeden Test.

Schritt 2: Ordnen Sie die p-Werte in absteigender Reihenfolge und weisen Sie jedem einen Rang zu: Der kleinste Wert hat den Rang 1, der nächstkleinere hat den Rang 2 usw.

Schritt 3: Berechnen Sie den kritischen Benjamini-Hochberg-Wert für jeden p-Wert mithilfe der Formel (i/m)*Q

Gold:

i = Rang des p-Werts

m = Gesamtzahl der Tests

Q = die von Ihnen gewählte Falscherkennungsrate

Schritt 4: Finden Sie den größten p-Wert, der kleiner als der kritische Wert ist. Bezeichnen Sie jeden p-Wert, der kleiner als dieser p-Wert ist, als signifikant.

Das folgende Beispiel veranschaulicht, wie Sie dieses Verfahren mit konkreten Werten durchführen.

Beispiel

Nehmen wir an, Forscher möchten herausfinden, ob 20 verschiedene Variablen mit Herzerkrankungen zusammenhängen. Sie führen jeweils 20 einzelne statistische Tests durch und erhalten für jeden Test einen p-Wert. Die folgende Tabelle zeigt die p-Werte für jeden Test, aufgelistet in absteigender Reihenfolge.

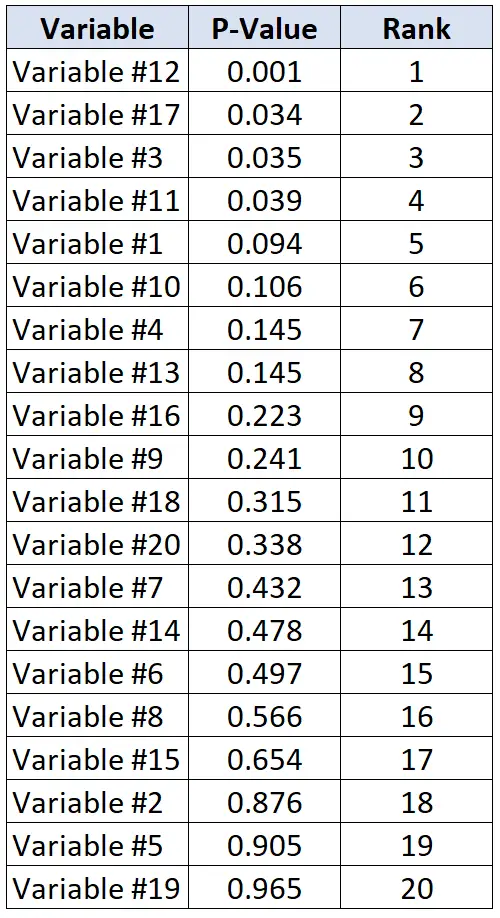
Angenommen, Forscher sind bereit, eine Falschentdeckungsrate von 20 % zu akzeptieren. Um den kritischen Benjamini-Hochberg-Wert für jeden p-Wert zu berechnen, können wir die folgende Formel verwenden: (i/20)*0,2 wobei i = Rang des p-Werts.

Die folgende Tabelle zeigt den kritischen Benjamini-Hochberg-Wert für jeden einzelnen p-Wert:

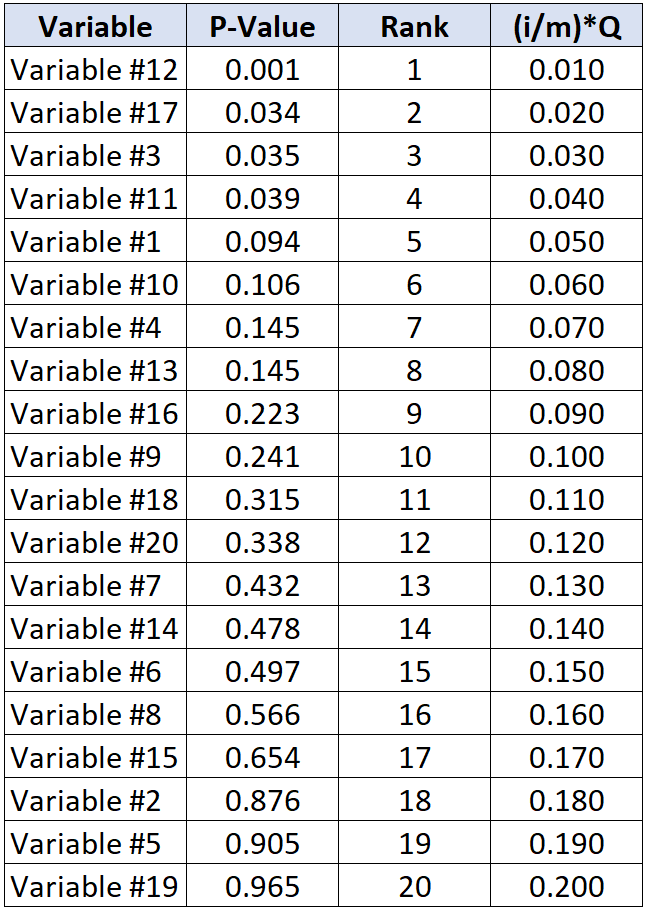
Der Test mit dem größten p-Wert unterhalb seines kritischen Benjamini-Hochberg-Werts ist Variable Nr. 11, die einen p-Wert von 0,039 und einen kritischen BH-Wert von 0,040 aufweist.

Daher werden dieser Test und alle Tests mit einem kleineren p-Wert als signifikant angesehen.

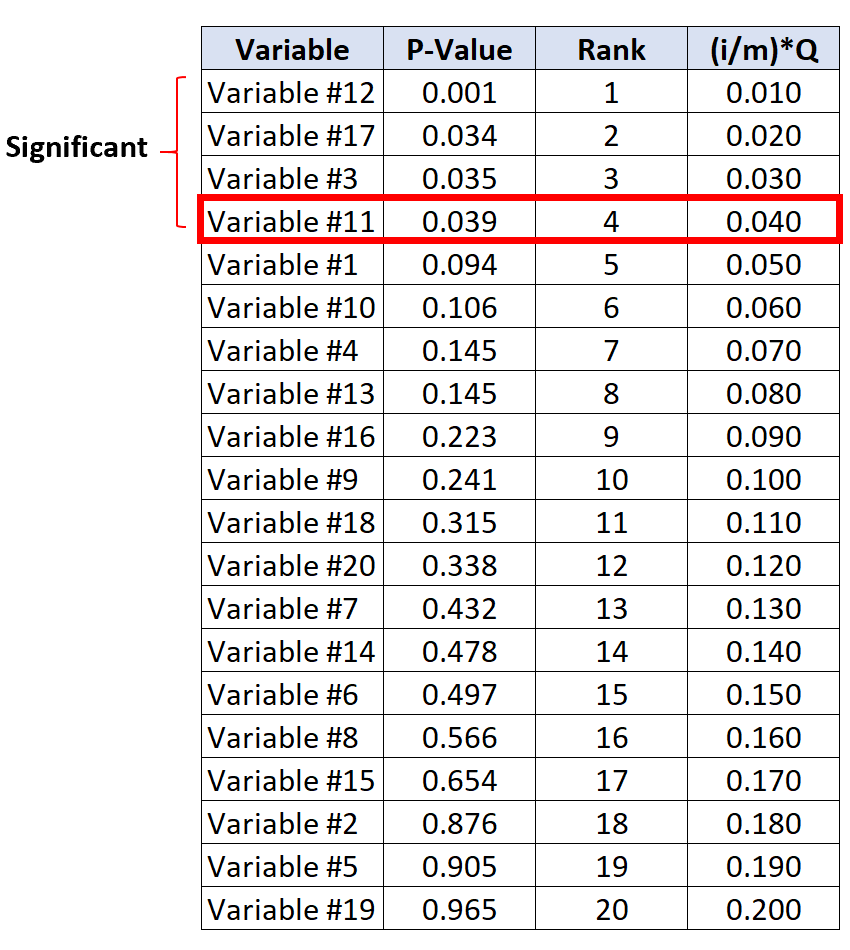
Beachten Sie, dass die Variablen Nr. 17 und Nr. 3 zwar keine p-Werte hatten, die kleiner als ihre kritischen BH-Werte waren, sie jedoch dennoch als signifikant angesehen werden, da sie kleinere p-Werte als Variable Nr. 11 haben.

So wählen Sie eine Falscherkennungsrate aus

Einer der wichtigsten Schritte im Benjamini-Hochberg-Verfahren ist die Wahl einer Falscherkennungsrate. Sie sollten Ihre Falscherkennungsrate auswählen, bevor Sie Daten sammeln oder statistische Tests durchführen.

In der Regel führen Sie während der explorativen Phase Ihrer Analyse eine große Anzahl statistischer Tests durch, an die Sie dann weitere Tests anschließen, um Ihre Ergebnisse weiter zu untersuchen.

Wenn Folgetests kostengünstig sind, sollten Sie erwägen, eine höhere Falscherkennungsrate festzulegen, denn selbst wenn Sie ein paar Fehlentdeckungen haben, werden Sie diese Falschentdeckungen wahrscheinlich bei nachfolgenden Tests entdecken.

Wenn außerdem die Kosten für das Verpassen einer wichtigen Entdeckung hoch sind, möchten Sie möglicherweise die Rate falscher Entdeckungen erhöhen, damit Ihnen nichts Wichtiges entgeht.

Abhängig von den Kosten Ihrer Recherche und davon, wie wichtig es ist, keine wichtigen Erkenntnisse zu übersehen, variiert die Rate falscher Entdeckungen von Situation zu Situation.

Zusätzliche Ressourcen

Eine Erklärung der P-Werte und der statistischen Signifikanz
Wie hoch ist die Fehlerquote pro Familie?