So berechnen sie p-werte in excel (3 beispiele)

In der Statistik verwenden wir Hypothesentests , um festzustellen, ob eine Aussage über einen Populationsparameter wahr ist oder nicht.

Wenn wir einen Hypothesentest durchführen, erhalten wir häufig eine T-Score-Teststatistik.

Sobald wir diese T-Score-Teststatistik gefunden haben, können wir den damit verbundenen p-Wert ermitteln.

Wenn dieser p-Wert kleiner als ein bestimmter Wert ist (z. B. 0,10, 0,05, 0,01), lehnen wir die Nullhypothese des Tests ab und kommen zu dem Schluss, dass unsere Ergebnisse statistisch signifikant sind.

Die folgenden Beispiele zeigen, wie in drei verschiedenen Szenarien ein p-Wert für eine Teststatistik in Excel berechnet wird.

Beispiel 1: Berechnen Sie den P-Wert für einen zweiseitigen Test

Angenommen, ein Botaniker möchte wissen, ob die durchschnittliche Höhe einer bestimmten Pflanzenart 15 Zoll beträgt.

In einer Zufallsstichprobe von 12 Pflanzen stellt sie fest, dass die durchschnittliche Höhe der Probe 14,33 Zoll und die Standardabweichung der Probe 1,37 Zoll beträgt.

Es führt einen Hypothesentest unter Verwendung der folgenden Null- und Alternativhypothesen durch:

H ₀ (Nullhypothese): μ= 15 Zoll

H _A (Alternativhypothese): μ ≠ 15 Zoll

Die Teststatistik wird wie folgt berechnet:

• t = ( X – µ) / (s/ √n )
• t = (14,33-15) / (1,37/√ 12 )
• t = -1,694

Die mit dieser Teststatistik verbundenen Freiheitsgrade sind n-1 = 12-1 = 11 .

Um den p-Wert für diese Teststatistik zu ermitteln, verwenden wir die folgende Formel in Excel:

 =T.DIST.2T(ABS(-1.694), 11)

Der folgende Screenshot zeigt, wie diese Formel in der Praxis angewendet wird.

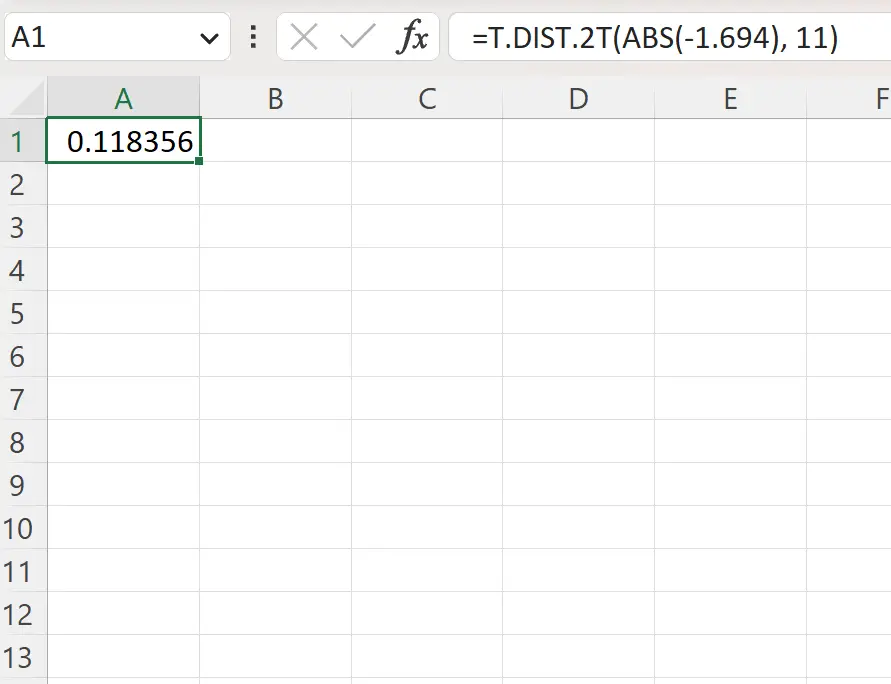
Der zweiseitige p-Wert beträgt 0,1184 .

Da dieser Wert nicht kleiner als 0,05 ist, können wir die Nullhypothese nicht ablehnen. Wir haben nicht genügend Beweise dafür, dass die durchschnittliche Pflanzenhöhe von 15 Zoll abweicht.

Beispiel 2: Berechnen Sie den P-Wert für den Test links

Nehmen wir an, dass das durchschnittliche Gewicht eines bestimmten Geräts, das in einer Fabrik hergestellt wird, 20 Gramm beträgt. Ein Prüfer schätzt das tatsächliche Durchschnittsgewicht jedoch auf weniger als 20 Gramm.

Um dies zu testen, wägt es eine einfache Zufallsstichprobe von 20 Widgets und erhält folgende Informationen:

• n = 20 Widgets
• x = 19,8 Gramm
• s = 3,1 Gramm

Anschließend wird ein Hypothesentest unter Verwendung der folgenden Null- und Alternativhypothesen durchgeführt:

H ₀ (Nullhypothese): μ ≥ 20 Gramm

H _A (Alternativhypothese): μ < 20 Gramm

Die Teststatistik wird wie folgt berechnet:

• t = ( X – µ) / (s/ √n )
• t = (19,8-20) / (3,1/√ 20 )
• t = -.2885

Die mit dieser Teststatistik verbundenen Freiheitsgrade sind n-1 = 20-1 = 19 .

Um den p-Wert für diese Teststatistik zu ermitteln, verwenden wir die folgende Formel in Excel:

 =T.DIST(-.2885, 19, TRUE)

Der folgende Screenshot zeigt, wie diese Formel in der Praxis angewendet wird.

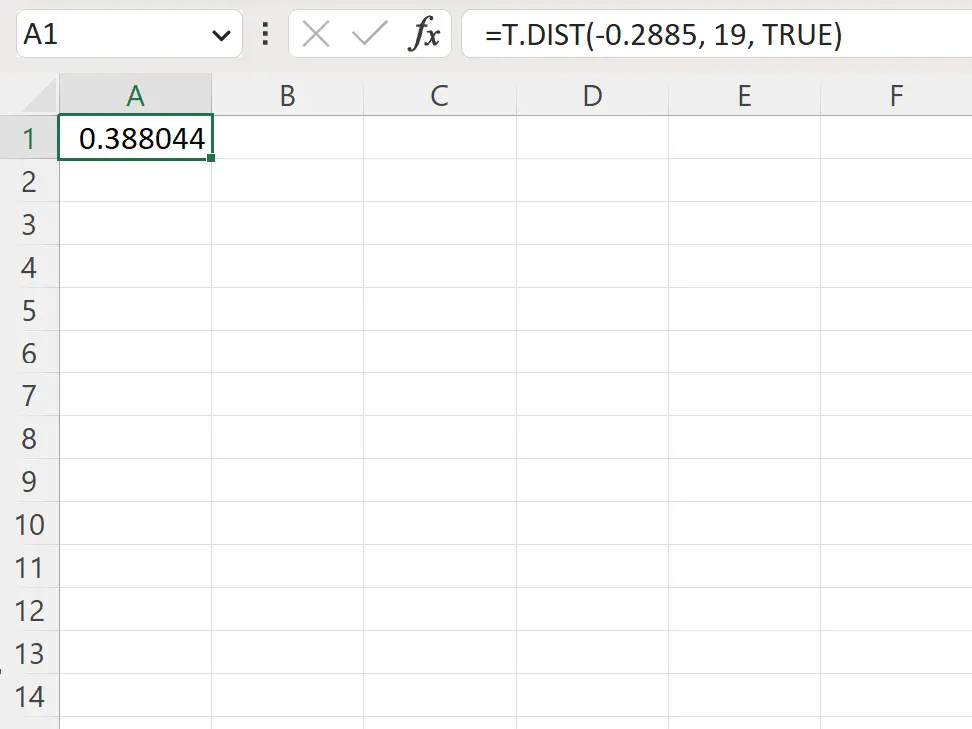
Der p-Wert auf der linken Seite beträgt 0,388044 .

Da dieser Wert nicht kleiner als 0,05 ist, kann der Inspektor die Nullhypothese nicht ablehnen. Es gibt keine ausreichenden Beweise dafür, dass das tatsächliche Durchschnittsgewicht der in dieser Fabrik hergestellten Produkte weniger als 20 Gramm beträgt.

Hinweis : Wir haben das Argument TRUE verwendet, um anzugeben, dass die kumulative Verteilungsfunktion bei der Berechnung des p-Werts verwendet werden soll.

Beispiel 3: Berechnen Sie den P-Wert für den rechtsseitigen Test

Nehmen wir an, dass die durchschnittliche Höhe einer bestimmten Pflanzenart 10 Zoll beträgt. Ein Botaniker sagt jedoch, dass die tatsächliche Durchschnittshöhe mehr als 10 Zoll beträgt.

Um diese Behauptung zu überprüfen, misst sie die Höhe einer einfachen Zufallsstichprobe von 15 Pflanzen und erhält folgende Informationen:

• n = 15 Pflanzen
• x = 11,4 Zoll
• s = 2,5 Zoll

Anschließend wird ein Hypothesentest unter Verwendung der folgenden Null- und Alternativhypothesen durchgeführt:

H ₀ (Nullhypothese): μ ≤ 10 Zoll

H _A (Alternativhypothese): μ > 10 Zoll

Die Teststatistik wird wie folgt berechnet:

• t = ( X – µ) / (s/ √n )
• t = (11,4-10) / (2,5/√ 15 )
• t = 2,1689

Die mit dieser Teststatistik verbundenen Freiheitsgrade sind n-1 = 15-1 = 14 .

Um den p-Wert für diese Teststatistik zu ermitteln, verwenden wir die folgende Formel in Excel:

 =T.DIST.RT(2.1689, 14)

Der folgende Screenshot zeigt, wie diese Formel in der Praxis angewendet wird.

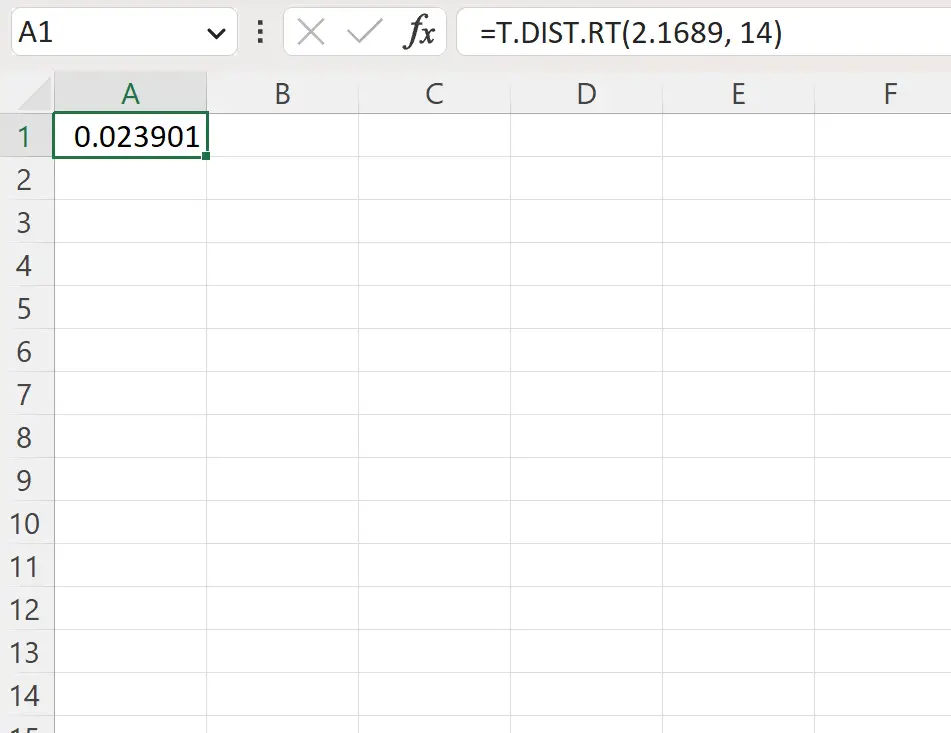
Der p-Wert auf der rechten Seite beträgt 0,023901 .

Da dieser Wert kleiner als 0,05 ist, kann der Botaniker die Nullhypothese ablehnen. Sie hat genügend Beweise, um zu sagen, dass die tatsächliche Durchschnittshöhe dieser Pflanzenart über 10 Zoll beträgt.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere häufige Aufgaben in Excel ausführen:

So ermitteln Sie einen P-Wert aus einem Z-Score in Excel
So ermitteln Sie den P-Wert einer F-Statistik in Excel
So ermitteln Sie den P-Wert einer Chi-Quadrat-Statistik in Excel