Bernoulli-verteilung und binomialverteilung: was ist der unterschied?

Eine Zufallsvariable folgt einer Bernoulli-Verteilung , wenn sie nur zwei mögliche Ergebnisse hat: 0 oder 1.

Angenommen, wir werfen einmal eine Münze. Sei p . Das bedeutet, dass die Wahrscheinlichkeit, dass es „Fails“ landet, 1- p beträgt.

Wir könnten also schreiben:

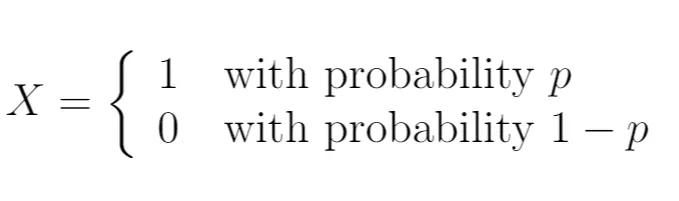
In diesem Fall folgt die Zufallsvariable X einer Bernoulli-Verteilung. Es kann nur zwei mögliche Werte annehmen.

Wenn wir nun eine Münze mehrmals werfen, folgt die Summe der Bernoulli-Zufallsvariablen einer Binomialverteilung.

Angenommen, wir werfen eine Münze fünfmal und möchten wissen, wie wahrscheinlich es ist, k- mal Kopf zu bekommen. Es sieht aus wie die Zufallsvariable

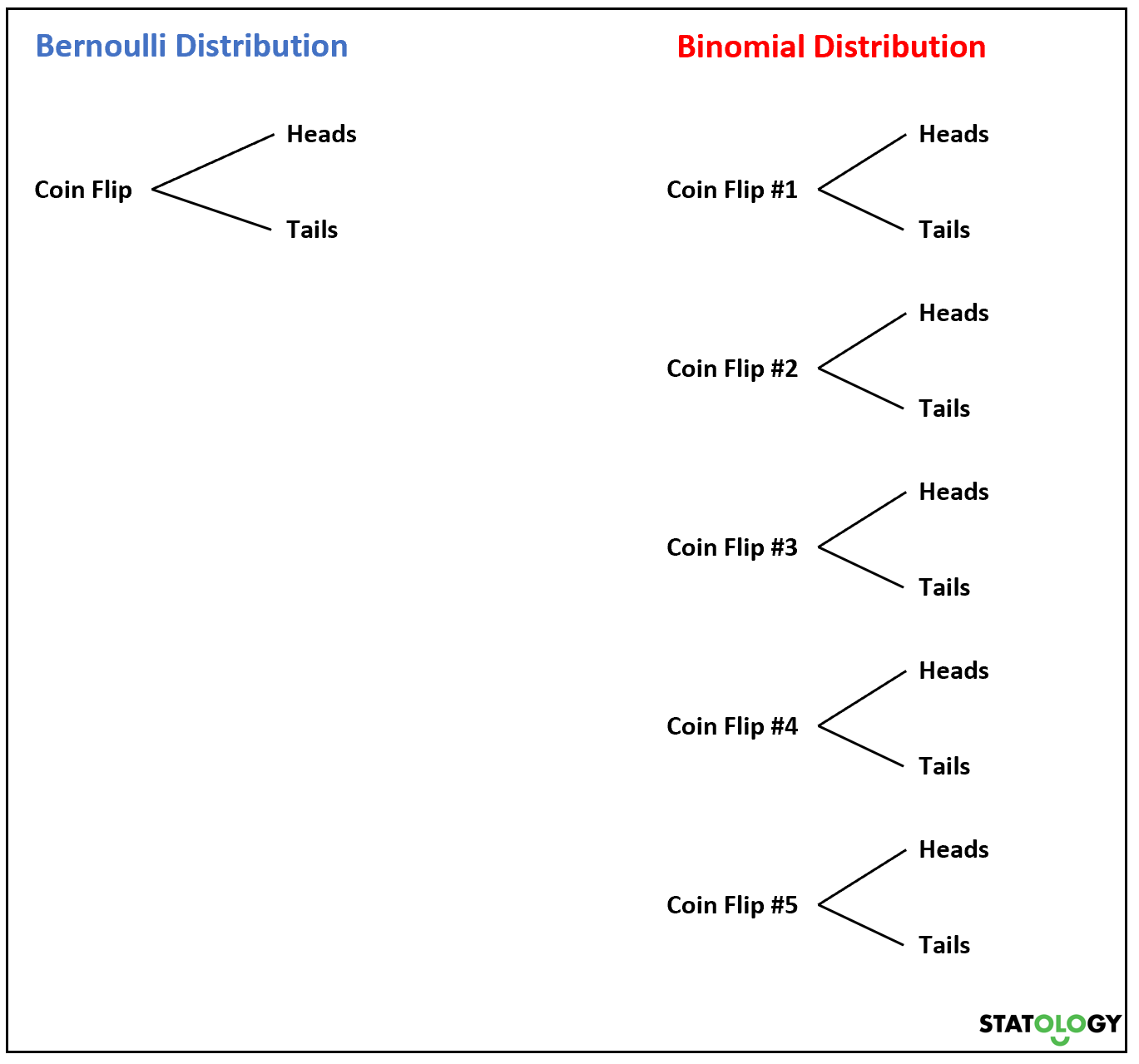
Wenn eine Zufallsvariable X einer Binomialverteilung folgt, kann die Erfolgswahrscheinlichkeit von X = k mit der folgenden Formel ermittelt werden:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

Gold:

• n: Anzahl der Versuche
• k: Anzahl der Erfolge
• p: Erfolgswahrscheinlichkeit bei einem bestimmten Versuch
• _n C _k : die Anzahl der Möglichkeiten, in n Versuchen k Erfolge zu erzielen

Angenommen, wir werfen dreimal eine Münze. Wir können die obige Formel verwenden, um die Wahrscheinlichkeit zu bestimmen, bei diesen drei Würfen 0 Köpfe zu bekommen:

P(X=0) = ₃ C ₀ * 0,5 ⁰ * (1-0,5) ^3-0 = 1 * 1 * (0,5) ³ = 0,125

Bei n = 1 Versuch entspricht die Binomialverteilung der Bernoulli-Verteilung.

Wichtige Notizen

Hier einige wichtige Hinweise zur Bernoulli- und Binomialverteilung:

1. Eine Zufallsvariable, die einer Bernoulli-Verteilung folgt, kann nur zwei mögliche Werte annehmen, eine Zufallsvariable, die einer Binomialverteilung folgt, kann jedoch mehrere Werte annehmen.

Beispielsweise haben wir bei einem einzelnen Münzwurf entweder 0 oder 1 Kopf. Allerdings könnten wir in einer Serie von 5 Unentschieden 0, 1, 2, 3, 4 oder 5 Köpfe haben.

2. Damit eine Zufallsvariable einer Binomialverteilung folgt, muss die Wahrscheinlichkeit des „Erfolgs“ in jedem Bernoulli-Versuch gleich und unabhängig sein.

Wenn wir beispielsweise „Erfolg“ als Kopflandung definieren, beträgt die Erfolgswahrscheinlichkeit bei jedem Wurf 0,5 und jeder Wurf ist unabhängig – das Ergebnis eines Wurfs hat keinen Einfluss auf das Ergebnis eines anderen.

Zusätzliche Ressourcen

Eine Einführung in Binomialexperimente
Eine Einführung in die Binomialverteilung
Die Form einer Binomialverteilung verstehen