Bestimmtheitsmaß (r im quadrat)
In diesem Artikel wird erklärt, was das Bestimmtheitsmaß (oder R-Quadrat) in der Statistik ist. So erfahren Sie, wie Sie das Bestimmtheitsmaß berechnen, wie es interpretiert wird und darüber hinaus einen Online-Rechner zur Berechnung des Bestimmtheitsmaßes einer Datenstichprobe.
Was ist das Bestimmtheitsmaß (R im Quadrat)?
Das Bestimmtheitsmaß , dessen Symbol R 2 ( R-Quadrat ) ist, ist eine Statistik, die die Anpassungsgüte eines Regressionsmodells misst. Das Bestimmtheitsmaß zeigt an, wie gut ein Regressionsmodell zu einem Datensatz passt, d. h. es gibt den Prozentsatz an, der durch das Regressionsmodell erklärt wird.
Daher ist das Regressionsmodell umso besser, je höher das Bestimmtheitsmaß ist. Obwohl diese Bedingung nicht immer erfüllt ist, sind wir grundsätzlich an einem möglichst großen Bestimmtheitsmaß interessiert. Im Folgenden erfahren Sie, wie das Bestimmtheitsmaß zu interpretieren ist.
Formel zur Bestimmung des Koeffizienten
Das Bestimmtheitsmaß ist gleich eins minus dem Verhältnis zwischen der Restvarianz und der Varianz der abhängigen Variablen. Das Bestimmtheitsmaß kann auch berechnet werden, indem man von den Residuen über die Gesamtsumme der Quadrate eins minus die Summe der Quadrate subtrahiert.
Somit lautet die Formel zur Berechnung des Bestimmtheitsmaßes wie folgt:

Gold:
-

ist das Bestimmtheitsmaß.
-
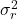
ist die Restvarianz.
-

ist die Varianz der abhängigen Variablen Y.
-
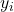
ist der Wert der beobachtungsabhängigen Variablen i.
-
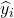
ist der durch das Regressionsmodell für Beobachtung i angenäherte Wert.
-

ist der Mittelwert der abhängigen Variablen über alle Beobachtungen.
👉 Mit dem Rechner unten können Sie das Bestimmtheitsmaß für jeden Datensatz berechnen.
Beim linearen Regressionsmodell entspricht das Bestimmtheitsmaß dem Quadrat des Korrelationskoeffizienten :
![]()
Gold
![]()
ist die Kovarianz der Variablen X und Y,
![]()
Und
![]()
sind die Varianzen der unabhängigen Variablen X bzw. der abhängigen Variablen Y.
Bestimmtheitsmaßrechner
Geben Sie Beispieldaten in den Rechner unten ein, um ein einfaches lineares Regressionsmodell anzupassen und dessen Bestimmtheitsmaß zu berechnen. Sie müssen die Datenpaare trennen, sodass im ersten Feld nur die Werte der unabhängigen Variablen X und im zweiten Feld nur die Werte der abhängigen Variablen Y stehen.
Die Daten müssen durch ein Leerzeichen getrennt und mit dem Punkt als Dezimaltrennzeichen eingegeben werden.
Interpretation des Bestimmtheitsmaßes
In diesem Abschnitt erfahren Sie, wie das Bestimmtheitsmaß zu interpretieren ist, da es keinen Sinn macht, den Wert des Bestimmtheitsmaßes zu kennen, wenn Sie später nicht wissen, was es bedeutet.
Der Wert des Bestimmtheitsmaßes kann zwischen 0 und 1 liegen, wird jedoch normalerweise in Prozent ausgedrückt, sodass das Minimum 0 % und das Maximum 100 % beträgt.
Was die Interpretation des Bestimmtheitsmaßes betrifft, bedeutet ein höherer Wert, dass das Regressionsmodell die Datenstichprobe besser erklärt. Je näher das Bestimmtheitsmaß also bei 1 liegt, desto stärker wird das Modell angepasst. Andererseits ist das erstellte Regressionsmodell umso weniger zuverlässig, je näher es bei 0 liegt.
Beim Vergleich zweier Regressionsmodelle ist jedoch nicht immer das Modell mit einem höheren Regressionskoeffizienten besser. Beispielsweise kann ein Regressionsmodell einen Regressionskoeffizienten R 2 = 100 % haben, da dem Modell viele erklärende Variablen hinzugefügt wurden und es daher alle Beobachtungen perfekt erklären kann. Aber dieses Modell liefert sicherlich eine sehr schlechte Vorhersage für einen neuen Wert, der nicht zur Erstellung des Regressionsmodells verwendet wurde.
Es sollte auch berücksichtigt werden, dass das resultierende Regressionsmodell die vorherigen Annahmen erfüllt. Daher ist ein Modell mit einem sehr hohen Bestimmtheitsmaß nutzlos, wenn die Variabilität seiner Residuen nicht konstant ist (Homoskedastizität).
Darüber hinaus stellt das Bestimmtheitsmaß eine wichtige Grenze dar, da es die Einbeziehung erklärender Variablen nicht beeinträchtigt. Logischerweise gilt: Je mehr erklärende Variablen ein Regressionsmodell hat, desto komplexer ist das Modell, aber desto besser erklärt es die beobachteten Daten und desto höher ist daher das Bestimmtheitsmaß. Das angepasste Bestimmtheitsmaß berücksichtigt jedoch die Anzahl der Variablen im Modell (wie es berechnet wird, sehen wir weiter unten).
Zusammenfassend lässt sich sagen, dass das Bestimmtheitsmaß für die Analyse eines Regressionsmodells sehr nützlich ist, da es uns Aufschluss darüber gibt, wie gut das Regressionsmodell zum Datensatz passt. Zur Überprüfung des resultierenden Modells sollten jedoch auch andere Tools verwendet werden, beispielsweise statistische Diagramme .
Angepasster Bestimmungskoeffizient
Das angepasste Bestimmtheitsmaß , auch angepasstes Bestimmtheitsmaß genannt, misst die Anpassungsgüte eines Regressionsmodells, indem es die Anzahl der im Modell enthaltenen erklärenden Variablen berücksichtigt.
Der Unterschied zwischen dem Bestimmtheitsmaß und dem angepassten Bestimmtheitsmaß besteht darin, dass das Bestimmtheitsmaß die Qualität der Anpassung misst, ohne die Anzahl der Variablen zu berücksichtigen, wohingegen das angepasste Bestimmtheitsmaß die Qualität der Anpassung misst Bestrafung für jede hinzugefügte Variable.
Die Formel zur Berechnung des angepassten Bestimmtheitsmaßes lautet wie folgt:
![]()
Gold:
-

ist das angepasste Bestimmtheitsmaß.
-

ist das Bestimmtheitsmaß.
-

ist die Stichprobengröße.
-

ist die Anzahl der erklärenden Variablen im Regressionsmodell.
Daher ist das angepasste Bestimmtheitsmaß besser als das Bestimmtheitsmaß für den Vergleich zweier verschiedener Modelle, da die Modelle eine unterschiedliche Anzahl erklärender Variablen haben können.