Was ist ein beta-level in der statistik? (definition & #038; beispiel)

In der Statistik verwenden wir Hypothesentests , um festzustellen, ob eine Hypothese über einen Populationsparameter wahr ist.

Ein Hypothesentest hat immer die folgenden zwei Hypothesen:

Nullhypothese (H ₀ ): Die Stichprobendaten stimmen mit der vorherrschenden Überzeugung bezüglich des Populationsparameters überein.

Alternativhypothese ( _HA ): Die Beispieldaten legen nahe, dass die in der Nullhypothese dargelegte Hypothese nicht wahr ist. Mit anderen Worten: Eine nicht zufällige Ursache beeinflusst die Daten.

Wann immer wir einen Hypothesentest durchführen, gibt es immer vier mögliche Ergebnisse:

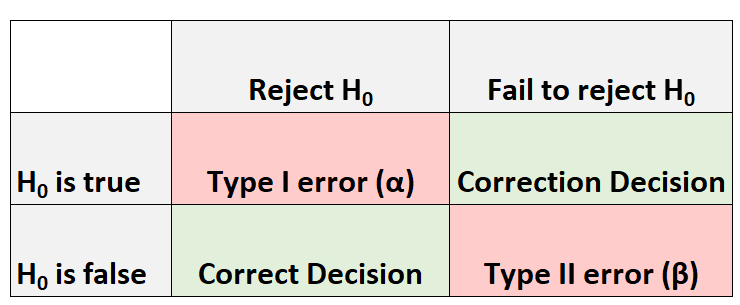
Es gibt zwei Arten von Fehlern, die wir machen können:

• Fehler vom Typ I: Wir lehnen die Nullhypothese ab, wenn sie tatsächlich wahr ist. Die Wahrscheinlichkeit dieses schwerwiegenden Fehlertyps wird mit α bezeichnet.
• Fehler vom Typ II: Wir können die Nullhypothese nicht ablehnen, wenn sie tatsächlich falsch ist. Die Wahrscheinlichkeit dieses begehenden Fehlertyps wird mit β angegeben.

Die Beziehung zwischen Alpha und Beta

Im Idealfall möchten Forscher, dass die Wahrscheinlichkeit, einen Fehler vom Typ I zu machen , und die Wahrscheinlichkeit, einen Fehler vom Typ II zu machen, gering ist.

Es gibt jedoch einen Kompromiss zwischen diesen beiden Wahrscheinlichkeiten. Wenn wir das Alpha-Niveau verringern, verringern wir möglicherweise die Wahrscheinlichkeit, eine Nullhypothese abzulehnen, wenn sie tatsächlich wahr ist. Dies erhöht jedoch tatsächlich das Beta-Niveau – die Wahrscheinlichkeit, dass wir die Nullhypothese nicht ablehnen, wenn sie falsch ist.

Die Beziehung zwischen Leistung und Beta

Die Aussagekraft eines Hypothesentests bezieht sich auf die Wahrscheinlichkeit, einen Effekt oder Unterschied zu erkennen, wenn ein Effekt oder Unterschied tatsächlich vorhanden ist. Mit anderen Worten: Es handelt sich um die Wahrscheinlichkeit, eine falsche Nullhypothese korrekt abzulehnen.

Es wird wie folgt berechnet:

Leistung = 1 – β

Im Allgemeinen möchten Forscher, dass die Aussagekraft eines Tests hoch ist, sodass der Test einen Effekt oder Unterschied erkennen kann, wenn es einen Effekt oder Unterschied gibt.

Aus der obigen Gleichung können wir erkennen, dass der beste Weg, die Aussagekraft eines Tests zu erhöhen, darin besteht, den Beta-Level zu reduzieren. Und der beste Weg, den Beta-Wert zu senken, besteht normalerweise darin, die Stichprobengröße zu erhöhen.

Die folgenden Beispiele zeigen, wie der Beta-Wert eines Hypothesentests berechnet wird, und zeigen, warum eine Erhöhung der Stichprobengröße den Beta-Wert verringern kann.

Beispiel 1: Beta für einen Hypothesentest berechnen

Angenommen, ein Forscher möchte testen, ob das durchschnittliche Gewicht der in einer Fabrik hergestellten Widgets weniger als 500 Unzen beträgt. Wir wissen, dass die Standardabweichung der Gewichte 24 Unzen beträgt, und der Forscher beschließt, eine Zufallsstichprobe von 40 Widgets zu sammeln.

Es wird die folgende Hypothese bei α = 0,05 verwirklichen:

• H ₀ : µ = 500
• _HA : μ < 500

Stellen Sie sich nun vor, dass das durchschnittliche Gewicht der produzierten Widgets tatsächlich 490 Unzen beträgt. Mit anderen Worten: Die Nullhypothese muss abgelehnt werden.

Wir können die folgenden Schritte verwenden, um das Beta-Niveau zu berechnen – die Wahrscheinlichkeit, die Nullhypothese nicht abzulehnen, obwohl sie tatsächlich abgelehnt werden sollte:

Schritt 1: Suchen Sie den Bereich ohne Ablehnung.

Laut dem Rechner für den kritischen Z-Wert beträgt der linke kritische Wert bei α = 0,05 -1,645 .

Schritt 2: Finden Sie die Mindeststichprobe, die wir nicht ablehnen.

Die Teststatistik wird berechnet als z = ( x – μ) / (s/ √n )

Wir können diese Gleichung also nach dem Stichprobenmittelwert lösen:

• x = µ – z*(s/ √n )
• x = 500 – 1,645*(24/ √40 )
• x = 493,758

Schritt 3: Bestimmen Sie die Wahrscheinlichkeit, dass der minimale Stichprobenmittelwert tatsächlich auftritt.

Wir können diese Wahrscheinlichkeit wie folgt berechnen:

• P(Z ≥ (493,758 – 490) / (24/√ 40 ))
• P(Z ≥ 0,99)

Gemäß dem normalen CDF-Rechner beträgt die Wahrscheinlichkeit, dass Z ≥ 0,99 ist, 0,1611 .

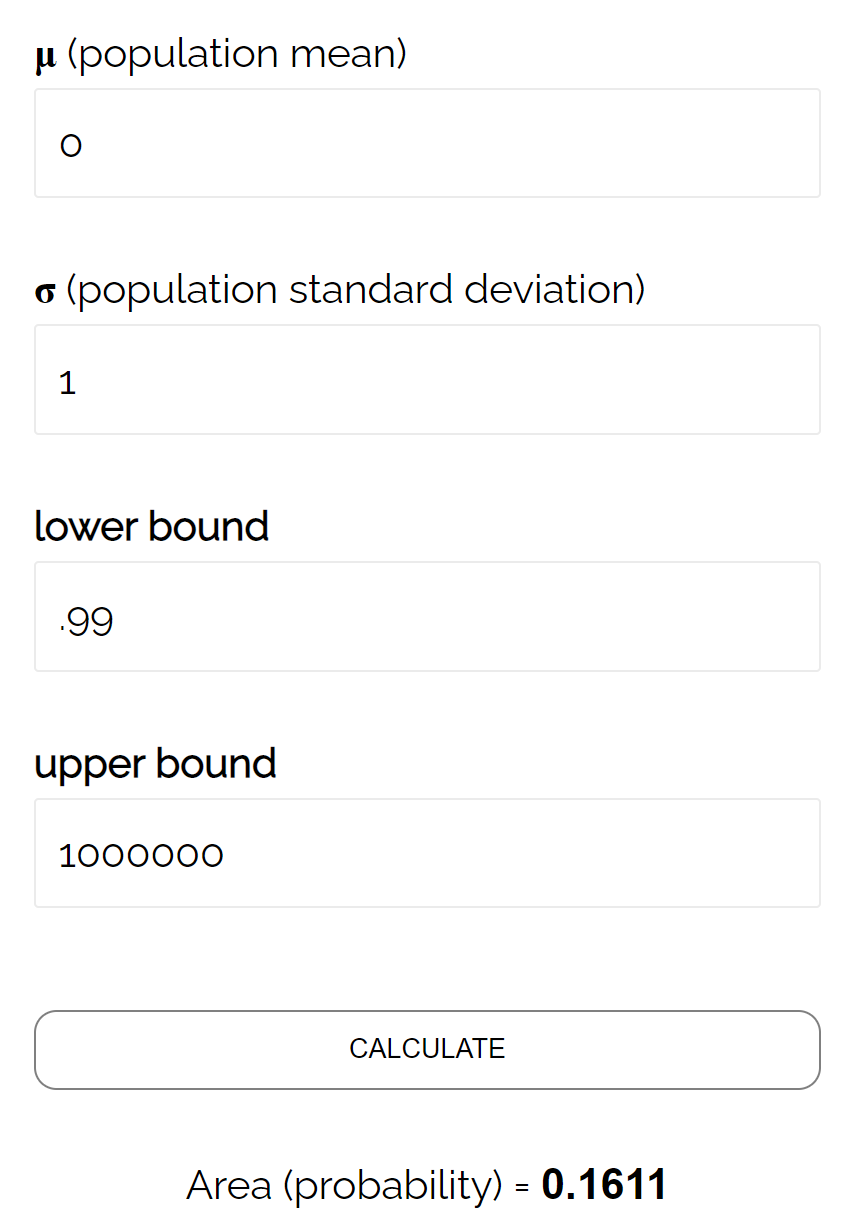
Somit beträgt der Beta-Wert für diesen Test β = 0,1611. Das bedeutet, dass die Wahrscheinlichkeit, den Unterschied nicht zu erkennen, bei 16,11 % liegt, wenn der tatsächliche Durchschnitt 490 Unzen beträgt.

Beispiel 2: Berechnen Sie Beta für einen Test mit einer größeren Stichprobengröße

Angenommen, der Forscher führt genau denselben Hypothesentest durch, verwendet jedoch stattdessen eine Stichprobe von n = 100 Widgets. Wir können dieselben drei Schritte wiederholen, um den Beta-Level für diesen Test zu berechnen:

Schritt 1: Suchen Sie den Bereich ohne Ablehnung.

Laut dem Rechner für den kritischen Z-Wert beträgt der linke kritische Wert bei α = 0,05 -1,645 .

Schritt 2: Finden Sie die Mindeststichprobe, die wir nicht ablehnen.

Die Teststatistik wird berechnet als z = ( x – μ) / (s/ √n )

Wir können diese Gleichung also nach dem Stichprobenmittelwert lösen:

• x = µ – z*(s/ √n )
• x = 500 – 1,645*(24/√ 100 )
• x = 496,05

Schritt 3: Bestimmen Sie die Wahrscheinlichkeit, dass der minimale Stichprobenmittelwert tatsächlich auftritt.

Wir können diese Wahrscheinlichkeit wie folgt berechnen:

• P(Z ≥ (496,05 – 490) / (24/√ 100 ))
• P(Z ≥ 2,52)

Laut dem normalen CDF-Rechner beträgt die Wahrscheinlichkeit, dass Z ≥ 2,52 ist , 0,0059.

Somit beträgt der Beta-Wert für diesen Test β = 0,0059. Das bedeutet, dass die Wahrscheinlichkeit, den Unterschied nicht zu erkennen, nur 0,59 % beträgt, wenn der tatsächliche Durchschnitt 490 Unzen beträgt.

Beachten Sie, dass der Forscher durch einfaches Erhöhen der Stichprobengröße von 40 auf 100 den Beta-Wert von 0,1611 auf 0,0059 senken konnte.

Bonus: Verwenden Sie diesen Typ-II-Fehlerrechner, um den Beta-Level eines Tests automatisch zu berechnen.

Zusätzliche Ressourcen

Einführung in das Testen von Hypothesen
So schreiben Sie eine Nullhypothese (5 Beispiele)
Eine Erklärung der P-Werte und der statistischen Signifikanz