Beta-verteilung
In diesem Artikel wird erklärt, was Beta-Distribution ist und wofür sie verwendet wird. Ebenso können Sie das Beta-Verteilungsdiagramm und die Eigenschaften dieser Art von Wahrscheinlichkeitsverteilung sehen.
Was ist die Beta-Verteilung?
Die Beta-Verteilung ist eine Wahrscheinlichkeitsverteilung, die auf dem Intervall (0,1) definiert und durch zwei positive Parameter parametrisiert ist: α und β. Mit anderen Worten, die Werte der Beta-Verteilung hängen von den Parametern α und β ab.
Daher besteht das Hauptmerkmal der Beta-Verteilung darin, dass ihre Form durch die Parameter α und β gesteuert werden kann. Darüber hinaus wird die Betaverteilung verwendet, um Zufallsvariablen zu definieren, deren Wert zwischen 0 und 1 liegt.
Es gibt mehrere Notationen, die darauf hinweisen, dass eine kontinuierliche Zufallsvariable durch eine Betaverteilung bestimmt wird. Die gebräuchlichsten sind:
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim B(\alpha,\beta)\\[2ex]X\sim Beta(\alpha,\beta)\\[2ex]X\sim \beta_{\alpha,\beta}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-ee1d0d8a1624a017b8ef9ce8a67c694e_l3.png)
In der Statistik hat die Beta-Verteilung sehr unterschiedliche Anwendungen. Beispielsweise wird die Betaverteilung verwendet, um prozentuale Schwankungen in verschiedenen Stichproben zu untersuchen. In ähnlicher Weise wird im Projektmanagement die Betaverteilung zur Durchführung einer Pert-Analyse verwendet.
Beta-Verteilungsdiagramm
Unter Berücksichtigung der Definition der Beta-Verteilung werden unten die Dichtefunktion und die Wahrscheinlichkeitsverteilungsfunktion der Beta-Verteilung dargestellt.
Unten sehen Sie, wie sich der Dichtefunktionsgraph der Beta-Verteilung in Abhängigkeit von den Parametern α und β ändert.
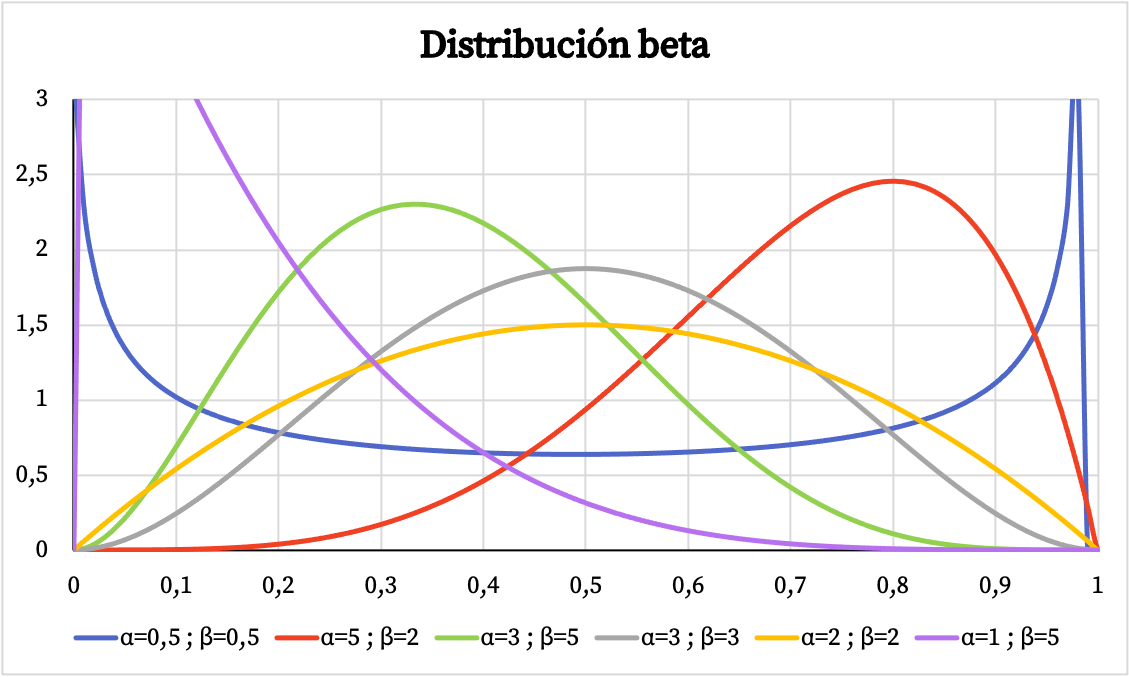
Ebenso sehen Sie unten die grafische Darstellung der kumulativen Wahrscheinlichkeit der Beta-Verteilung basierend auf den Parametern α und β.
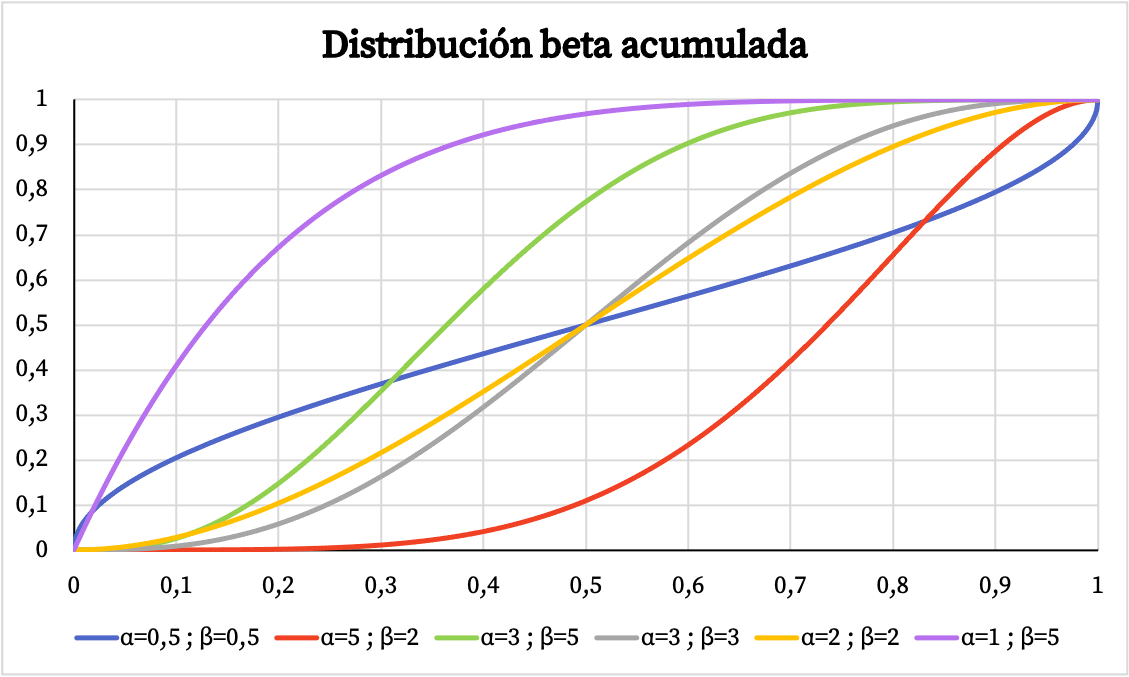
Merkmale der Beta-Verteilung
In diesem Abschnitt werden wir sehen, was die wichtigsten Merkmale der Beta-Verteilung sind.
- Die Parameter α und β der Betaverteilung sind reelle und positive Zahlen.
![\begin{array}{c}\alpha >0\\[2ex] \beta >0\end{array}“ title=“Rendered by QuickLaTeX.com“ height=“54″ width=“44″ style=“vertical-align: 0px;“></p>
</p>
<ul>
<li> Der Bereich der Betaverteilung reicht von 0 bis 1, die beiden Extreme sind nicht enthalten.</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-442bebaba847543d6db71cdf0127a4b0_l3.png)
![]()
- Der Mittelwert der Betaverteilung ist gleich Alpha dividiert durch die Summe Alpha plus Beta.
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim B(\alpha,\beta)\\[2ex] E[X]=\cfrac{\alpha}{\alpha+\beta}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-4530a8b72211111e8bec79b6388e00a7_l3.png)
- Die Varianz der Betaverteilung kann mit der folgenden Formel berechnet werden:
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim B(\alpha,\beta)\\[2ex] Var(X)=\cfrac{\alpha\cdot \beta}{(\alpha+\beta+1)\cdot (\alpha+\beta)^2}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-71c6ef40db833722e63c56cd763d6601_l3.png)
- Für Alpha- und Beta-Werte größer als 1 kann der Beta-Verteilungsmodus leicht mit dem folgenden Ausdruck ermittelt werden:
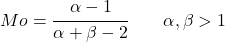
![]()
Dabei ist B(α,β) die Beta-Funktion, die wie folgt definiert ist:
![]()
- Die kumulative Wahrscheinlichkeitsfunktion der Betaverteilung ist:
![]()
Dabei ist B(x;α,β) die unvollständige Betafunktion, definiert als:
![]()
- Wenn X eine durch eine Beta-Verteilung definierte Variable ist, dann ist 1-X eine durch eine Beta-Verteilung definierte Variable, deren Alpha- und Beta-Parameter jeweils die Beta- und Alpha-Parameter der ursprünglichen Beta-Verteilung sind.
![]()
- Wenn die Alpha- und Beta-Parameter der Beta-Verteilung beide gleich 1 sind, entspricht die Verteilung einer gleichmäßigen Verteilung der Parameter 0 und 1.
![]()