Bevölkerung bedeutet

Von Dr. Benjamin Anderson August 3, 2023 Statistiken Keine Kommentare

In diesem Artikel wird erklärt, was Bevölkerung in der Statistik bedeutet. Ebenso erfahren Sie, wie die Formel für den Grundgesamtheitsmittelwert lautet, wie das Konfidenzintervall des Grundgesamtheitsmittelwerts berechnet wird und außerdem, wie groß der Unterschied zwischen dem Grundgesamtheitsmittelwert und dem Mittelwert der Stichprobe ist.

Wie hoch ist der Bevölkerungsdurchschnitt?

Der Populationsmittelwert ist der arithmetische Durchschnitt aller Elemente der statistischen Population. Um den Mittelwert der Grundgesamtheit zu berechnen, müssen daher alle Grundgesamtheitswerte addiert und dann durch die Gesamtzahl der Elemente in der Grundgesamtheit dividiert werden.

Das Symbol für den Bevölkerungsmittelwert ist der griechische Buchstabe μ.

Ebenso kann der Populationsmittelwert auch als der erwartete Wert der Variablen definiert werden, die eine Population darstellt.

So berechnen Sie den Bevölkerungsdurchschnitt

Nachdem wir die Definition des Bevölkerungsmittelwerts kennengelernt haben, sehen wir uns an, wie der Bevölkerungsmittelwert berechnet wird, um seine Bedeutung besser zu verstehen.

Wenn alle Werte in der statistischen Grundgesamtheit bekannt sind, sollte zur Berechnung des Grundgesamtheitsmittels einfach die arithmetische Mittelformel angewendet werden. In diesem Fall müssen wir zur Berechnung des Populationsmittelwerts alle Populationswerte addieren und dann durch die Gesamtzahl der Daten dividieren.

Wenn wir also den Wert aller Elemente der Grundgesamtheit kennen, lautet die Formel zur Berechnung des Mittelwerts der Grundgesamtheit wie folgt:

$\displaystyle\mu=\frac{\displaystyle \sum_{i=1}^N x_i}{N}=\frac{x_1+x_2+\dots +x_N}{N}$

➤ Siehe: Beispiel zur Berechnung des arithmetischen Mittels

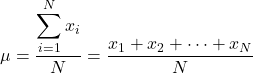
Allerdings sind im Allgemeinen nicht alle Bevölkerungswerte bekannt, daher wird der Wert des Bevölkerungsmittelwerts normalerweise anhand von Intervallen geschätzt .

Konfidenzintervall für den Bevölkerungsmittelwert

In der Praxis ist es unmöglich, alle Individuen einer Population zu untersuchen. Daher wird normalerweise eine Zufallsstichprobe der Population ausgewählt und auf der Grundlage ihrer Werte eine Annäherung an den Wert des Populationsmittelwerts vorgenommen. Genauer gesagt berechnen wir ein Intervall, in dem der Mittelwert der gesamten Grundgesamtheit mit hoher Wahrscheinlichkeit liegt; Dieses Intervall wird als Konfidenzintervall für den Grundgesamtheitsmittelwert bezeichnet.

Das Konfidenzintervall für den Grundgesamtheitsmittelwert wird berechnet, indem der Wert von Z _α/2 , multipliziert mit der Standardabweichung (σ) und durch die Quadratwurzel der Höhe der Stichprobe (n) addiert und vom Stichprobenmittelwert subtrahiert wird. Daher lautet die Formel zur Berechnung des Konfidenzintervalls für den Grundgesamtheitsmittelwert:

$\displaystyle \left(\overline{x}-z_{\alpha/2}\cdot \frac{\sigma}{\sqrt{n}} \ , \ \overline{x}+z_{\alpha/2}\cdot \frac{\sigma}{\sqrt{n}} \right)$

Die obige Formel wird verwendet, wenn die Populationsvarianz bekannt ist. Wenn jedoch die Populationsvarianz unbekannt ist, was am häufigsten der Fall ist, wird das Konfidenzintervall für den Mittelwert anhand der folgenden Formel berechnet:

$\displaystyle \left(\overline{x}-t_{\alpha/2}\cdot \frac{s}{\sqrt{n}} \ , \ \overline{x}+t_{\alpha/2}\cdot \frac{s}{\sqrt{n}} \right)$

Gold:

$\overline{x}$

ist das Beispielmittel.
$t_{\alpha/2}$

ist der Wert der Student-t-Verteilung von n-1 Freiheitsgraden mit der Wahrscheinlichkeit α/2. Bei großen Stichprobengrößen und einem Konfidenzniveau von 95 % liegt er normalerweise nahe bei 1,96 und bei einem Konfidenzniveau von 99 % normalerweise nahe bei 2,576.
$s$

ist die Standardabweichung der Stichprobe.
$n$

ist die Stichprobengröße.

➤ Siehe: Beispiel für die Berechnung des Konfidenzintervalls für den Grundgesamtheitsmittelwert

Populationsmittelwert und Stichprobenmittelwert

Abschließend werden wir zusammenfassend die Unterschiede zwischen dem Populationsmittelwert und dem Stichprobenmittelwert untersuchen, damit diese beiden statistischen Konzepte klarer werden.

Die Differenz zwischen dem Populationsmittelwert und dem Stichprobenmittelwert ist der Wertebereich, über den der Mittelwert berechnet wird. Der Grundgesamtheitsmittelwert ist der Durchschnitt der gesamten statistischen Grundgesamtheit, während der Stichprobenmittelwert der Durchschnitt einer Stichprobe der Grundgesamtheit ist.

Um den Populationsmittelwert vom Stichprobenmittelwert zu unterscheiden, werden sie außerdem durch unterschiedliche Symbole dargestellt. Das Symbol für die Bevölkerung bedeutet:

$\mu$

, hingegen ist das Symbol für den Stichprobenmittelwert

$\overline{x}$

$\begin{array}{c}\mu =\text{Media poblacional}\\[2ex]\overline{x} = \text{Media muestral}\end{array}$

Wenn Sie immer noch Zweifel an den Unterschieden zwischen diesen beiden Arten von Durchschnittswerten haben oder mehr über die Berechnung des Stichprobendurchschnitts erfahren möchten, können Sie den folgenden Artikel lesen:

➤ Siehe: Was ist der Stichprobenmittelwert?

Über den Autor

Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen