So führen sie eine zweifaktorielle anova in excel durch

Mithilfe einer zweifaktoriellen ANOVA („Varianzanalyse“) wird ermittelt, ob ein statistisch signifikanter Unterschied zwischen den Mittelwerten von drei oder mehr unabhängigen Gruppen besteht, die auf zwei Faktoren aufgeteilt wurden.

In diesem Tutorial wird erläutert, wie Sie eine zweifaktorielle ANOVA in Excel durchführen.

Beispiel: Zweifaktorielle ANOVA in Excel

Ein Botaniker möchte wissen, ob das Pflanzenwachstum durch die Sonneneinstrahlung und die Häufigkeit des Gießens beeinflusst wird. Sie pflanzt 40 Samen und lässt sie zwei Monate lang unter unterschiedlichen Bedingungen der Sonneneinstrahlung und Bewässerungshäufigkeit wachsen. Nach zwei Monaten zeichnet sie die Höhe jeder Pflanze auf. Die Ergebnisse sind unten dargestellt:

In der Tabelle oben sehen wir, dass in jeder Kombination von Bedingungen fünf Pflanzen gezüchtet wurden. Beispielsweise wurden fünf Pflanzen mit täglicher Bewässerung und ohne Sonnenlicht gezüchtet und ihre Höhen betrugen nach zwei Monaten 4,8 Zoll, 4,4 Zoll, 3,2 Zoll, 3,9 Zoll und 4,4 Zoll:

Mit den folgenden Schritten können wir eine zweifaktorielle ANOVA für diese Daten durchführen:

Schritt 1: Wählen Sie das Data Analysis Toolpak aus.

Klicken Sie auf der Registerkarte „Daten“ auf „Datenanalyse“ :

Wenn Sie dies nicht als Option sehen, sollten Sie zunächst das kostenlose Data Analysis Toolpak laden .

2. Wählen Sie Anova: zwei Faktoren mit Replikation

Wählen Sie die Option „Anova: Two-Factor With Replication“ aus und klicken Sie dann auf „OK“ .

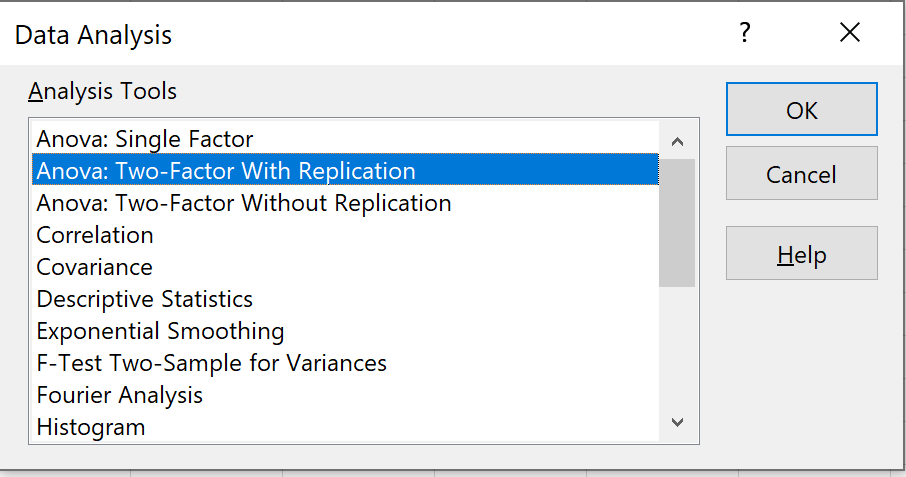
In diesem Zusammenhang bezieht sich „Replikation“ auf mehrere Beobachtungen in jeder Gruppe. Beispielsweise wurden viele Pflanzen ohne Sonneneinstrahlung und ohne tägliches Gießen gezüchtet. Wenn wir stattdessen in jeder Kombination von Bedingungen nur eine Pflanze anbauen würden, würden wir „keine Replikation“ verwenden, aber unsere Stichprobengröße wäre viel kleiner.

3. Geben Sie die erforderlichen Werte ein.

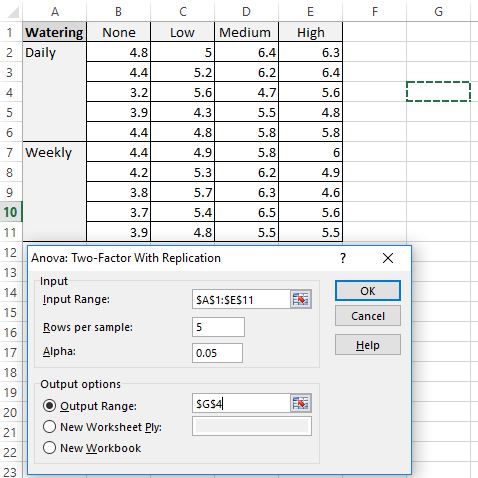
Geben Sie als Nächstes die folgenden Werte ein:

• Eingabebereich: Wählen Sie den Zellbereich aus, in dem sich unsere Daten befinden, einschließlich der Überschriften.
• Zeilen pro Probe: Geben Sie „5“ ein, da jede Probe 5 Pflanzen enthält.
• Alpha: Wählen Sie ein zu verwendendes Signifikanzniveau aus. Wir wählen 0,05.
• Ausgabebereich: Wählen Sie eine Zelle aus, in der die Ausgabe der bidirektionalen ANOVA angezeigt werden soll. Wir wählen Zelle $G$4.

Schritt 4: Interpretieren Sie das Ergebnis.

Sobald wir auf OK klicken, wird das Ergebnis der Zwei-Wege-ANOVA angezeigt:

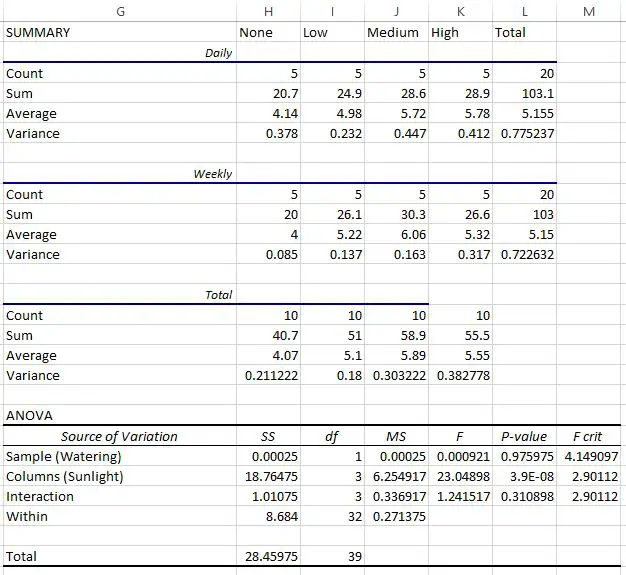
Die ersten drei Tabellen enthalten zusammenfassende Statistiken für jede Gruppe. Zum Beispiel:

• Die durchschnittliche Höhe der täglich bewässerten Pflanzen, jedoch ohne Sonnenlicht, betrug 4,14 Zoll.
• Die durchschnittliche Höhe der Pflanzen, die wöchentlich gegossen wurden und wenig Sonnenlicht erhielten, betrug 5,22 Zoll.
• Die durchschnittliche Höhe aller täglich bewässerten Pflanzen betrug 5,115 Zoll.
• Die durchschnittliche Höhe aller wöchentlich bewässerten Pflanzen betrug 5,15 Zoll.
• Die durchschnittliche Höhe aller Pflanzen bei starker Sonneneinstrahlung betrug 5,55 Zoll.

Und so weiter.

Die letzte Tabelle zeigt das Ergebnis der zweifaktoriellen ANOVA. Wir können Folgendes beobachten:

• Der p-Wert für die Wechselwirkung zwischen Bewässerungshäufigkeit und Sonneneinstrahlung betrug 0,310898 . Dies ist auf dem Alpha-Niveau von 0,05 statistisch nicht signifikant.
• Der p-Wert für die Bewässerungshäufigkeit betrug 0,975975 . Dies ist auf dem Alpha-Niveau von 0,05 statistisch nicht signifikant.
• Der p-Wert für Sonneneinstrahlung betrug 3,9E-8 (0,000000039) . Dies ist statistisch signifikant bei einem Alpha-Wert von 0,05.

Diese Ergebnisse deuten darauf hin, dass die Sonneneinstrahlung der einzige Faktor ist, der einen statistisch signifikanten Einfluss auf die Pflanzenhöhe hat. Und da es keinen Wechselwirkungseffekt gibt, ist der Effekt der Sonneneinstrahlung bei jeder Bewässerungshäufigkeit gleichbleibend. Einfach ausgedrückt: Ob eine Pflanze täglich oder wöchentlich gegossen wird, hat keinen Einfluss darauf, wie sich Sonneneinstrahlung auf eine Pflanze auswirkt.