So verwenden sie die binomialverteilung in google sheets
Die Binomialverteilung in der Statistik beschreibt die Wahrscheinlichkeit, in n Versuchen k Erfolge zu erzielen, wenn die Erfolgswahrscheinlichkeit in einem einzelnen Experiment p beträgt.
Um Binomialverteilungswahrscheinlichkeiten in Google Sheets zu berechnen, können wir die Funktion BINOMVERT verwenden, die die folgende grundlegende Syntax verwendet:
BINOMVERT(k, n, p, kumulativ)
Gold:
- k : Anzahl der Erfolge
- n : Anzahl der Versuche
- p : Erfolgswahrscheinlichkeit bei einem bestimmten Test
- kumulativ : ob eine kumulative Wahrscheinlichkeit berechnet werden soll (Standardwert ist FALSE)
Die folgenden Beispiele zeigen, wie Sie diese Funktion in der Praxis nutzen können.
Beispiel 1: Wahrscheinlichkeit von genau k Erfolgen
Ty macht 60 % seiner Freiwurfversuche. Wenn er 12 Freiwürfe macht, wie groß ist dann die Wahrscheinlichkeit, dass er genau 10 macht?
Um diese Frage zu beantworten, können wir die folgende Formel in Google Sheets verwenden:
= BINOMDIST ( 10,12,0.6 , FALSE ) _ _ _ _
Der folgende Screenshot zeigt, wie diese Formel in der Praxis angewendet wird:
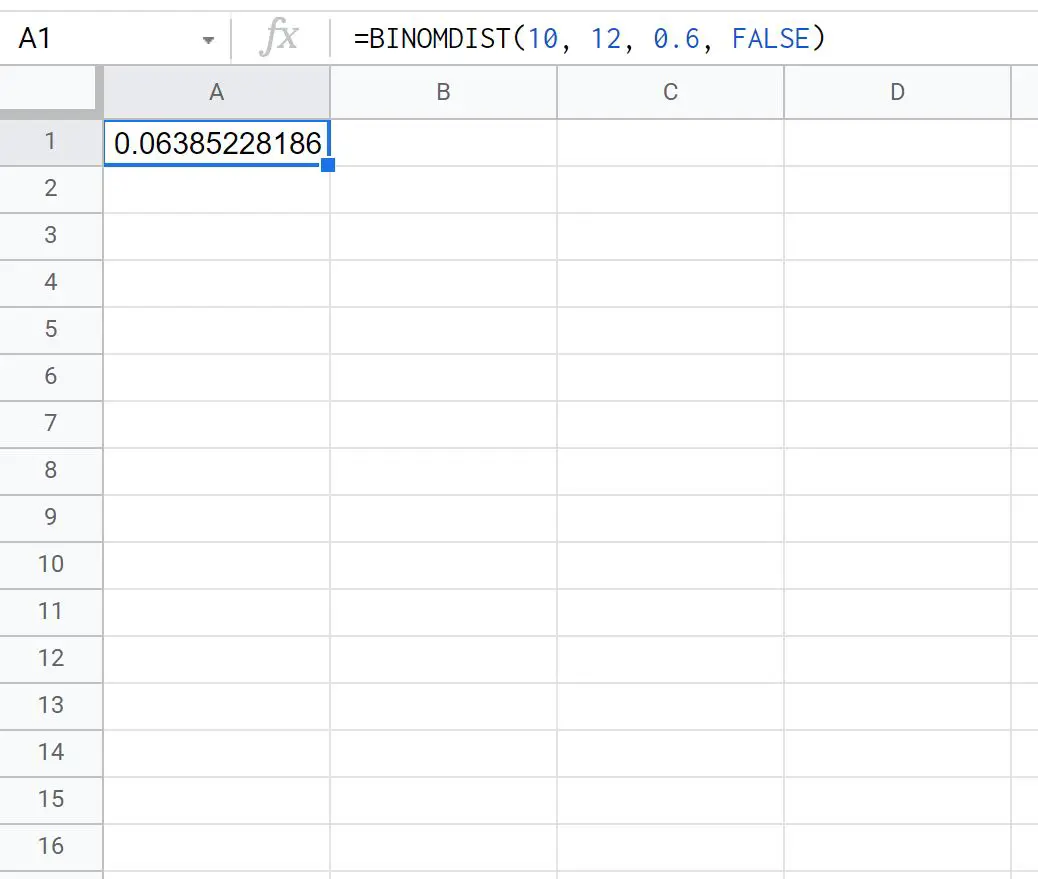
Die Wahrscheinlichkeit, dass Ty genau 10 von 12 Freiwurfversuchen macht, beträgt 0,0639 .
Beispiel 2: Erfolgswahrscheinlichkeit kleiner als k
Ty macht 60 % seiner Freiwurfversuche. Wenn er 12 Freiwürfe macht, wie groß ist dann die Wahrscheinlichkeit, dass er weniger als 10 macht?
Um diese Frage zu beantworten, können wir die folgende Formel in Google Sheets verwenden:
= BINOMDIST ( 9,12,0.6 , TRUE ) _ _ _ _
Der folgende Screenshot zeigt, wie diese Formel in der Praxis angewendet wird:
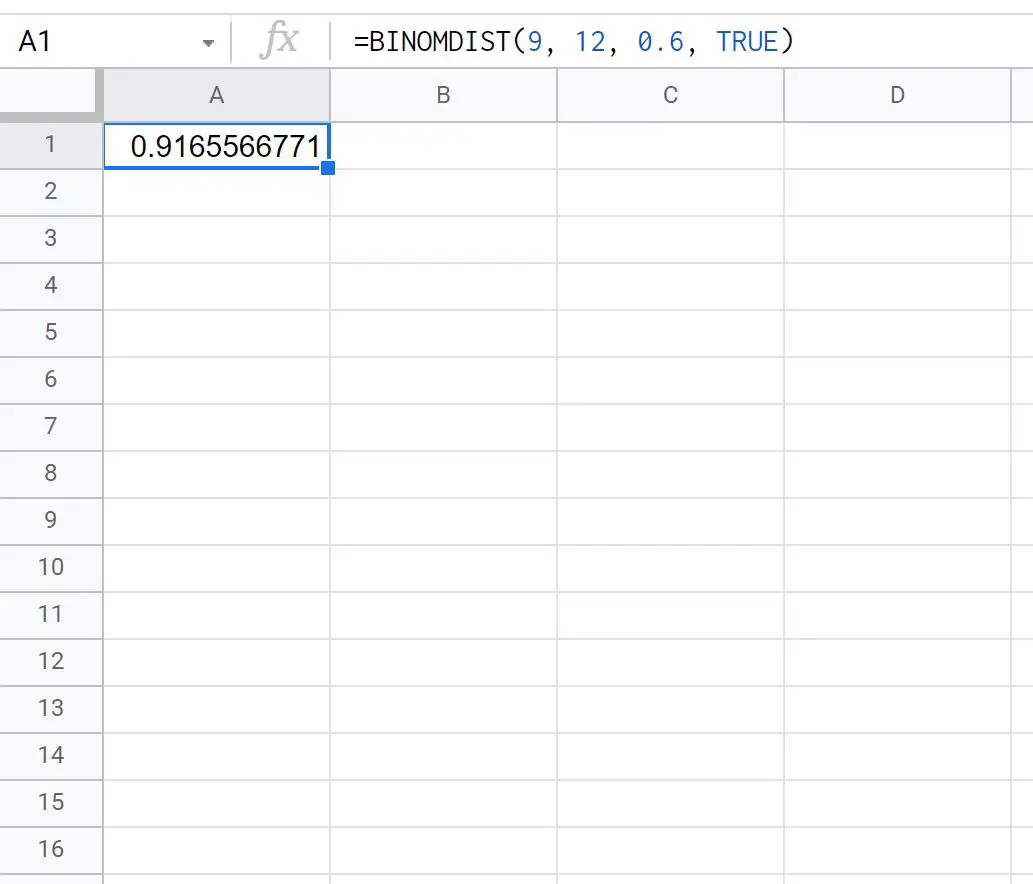
Die Wahrscheinlichkeit, dass Ty weniger als 10 von 12 Freiwurfversuchen macht, beträgt 0,9166 .
Beispiel 3: Wahrscheinlichkeit kleiner oder gleich k Erfolg
Ty macht 60 % seiner Freiwurfversuche. Wenn er 12 Freiwürfe macht, wie hoch ist dann die Wahrscheinlichkeit, dass er weniger als oder gleich 10 macht?
Um diese Frage zu beantworten, können wir die folgende Formel in Google Sheets verwenden:
= BINOMDIST ( 10,12,0.6 , TRUE ) _ _ _ _
Der folgende Screenshot zeigt, wie diese Formel in der Praxis angewendet wird:
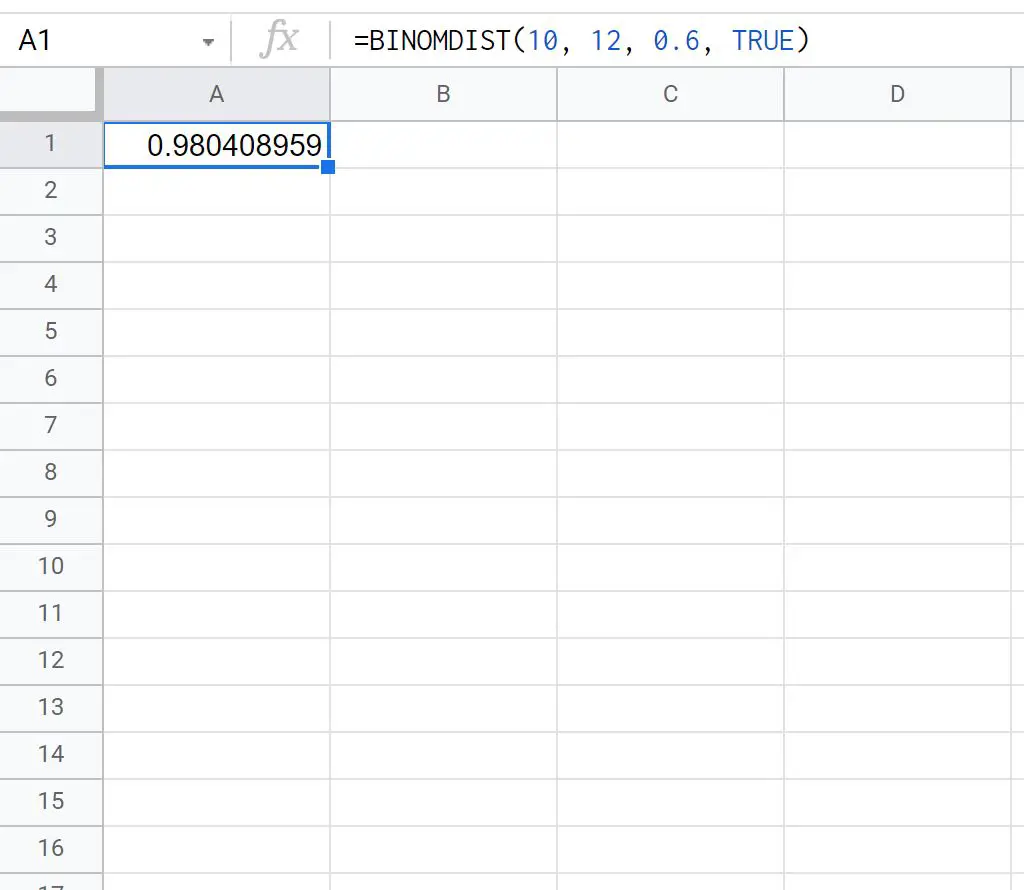
Die Wahrscheinlichkeit, dass Ty weniger als oder gleich 10 von 12 Freiwurfversuchen macht, beträgt 0,9166 .
Beispiel 4: Wahrscheinlichkeit eines größeren Erfolgs
Ty macht 60 % seiner Freiwurfversuche. Wenn er 12 Freiwürfe macht, wie hoch ist dann die Wahrscheinlichkeit, dass er mehr als 10 macht?
Um diese Frage zu beantworten, können wir die folgende Formel in Google Sheets verwenden:
=1- BINOMDIST ( 10 , 12 , 0.6 , TRUE )
Der folgende Screenshot zeigt, wie diese Formel in der Praxis angewendet wird:
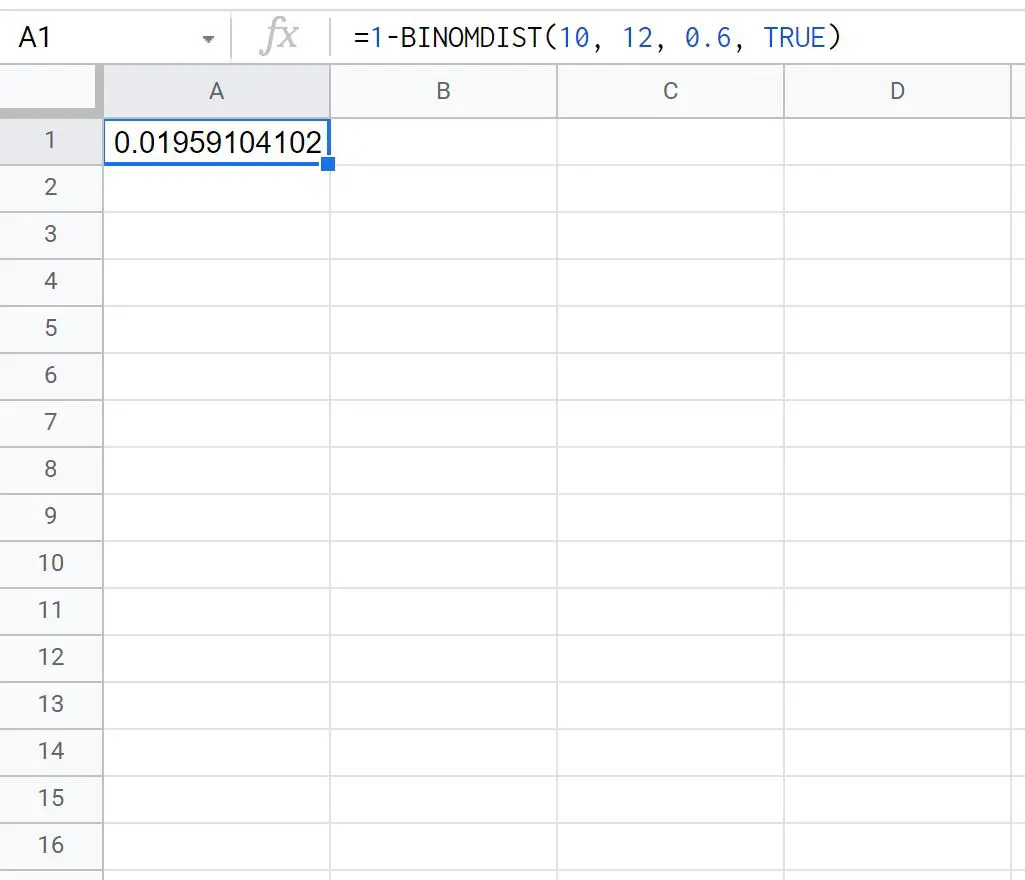
Die Wahrscheinlichkeit, dass Ty mehr als 10 von 12 Freiwurfversuchen macht, beträgt 0,0196 .
Beispiel 5: Erfolgswahrscheinlichkeit größer oder gleich k
Ty macht 60 % seiner Freiwurfversuche. Wenn er 12 Freiwürfe macht, wie groß ist dann die Wahrscheinlichkeit, dass er insgesamt 10 oder mehr macht?
Um diese Frage zu beantworten, können wir die folgende Formel in Google Sheets verwenden:
=1- BINOMDIST ( 9 , 12 , 0.6 , TRUE )
Der folgende Screenshot zeigt, wie diese Formel in der Praxis angewendet wird:
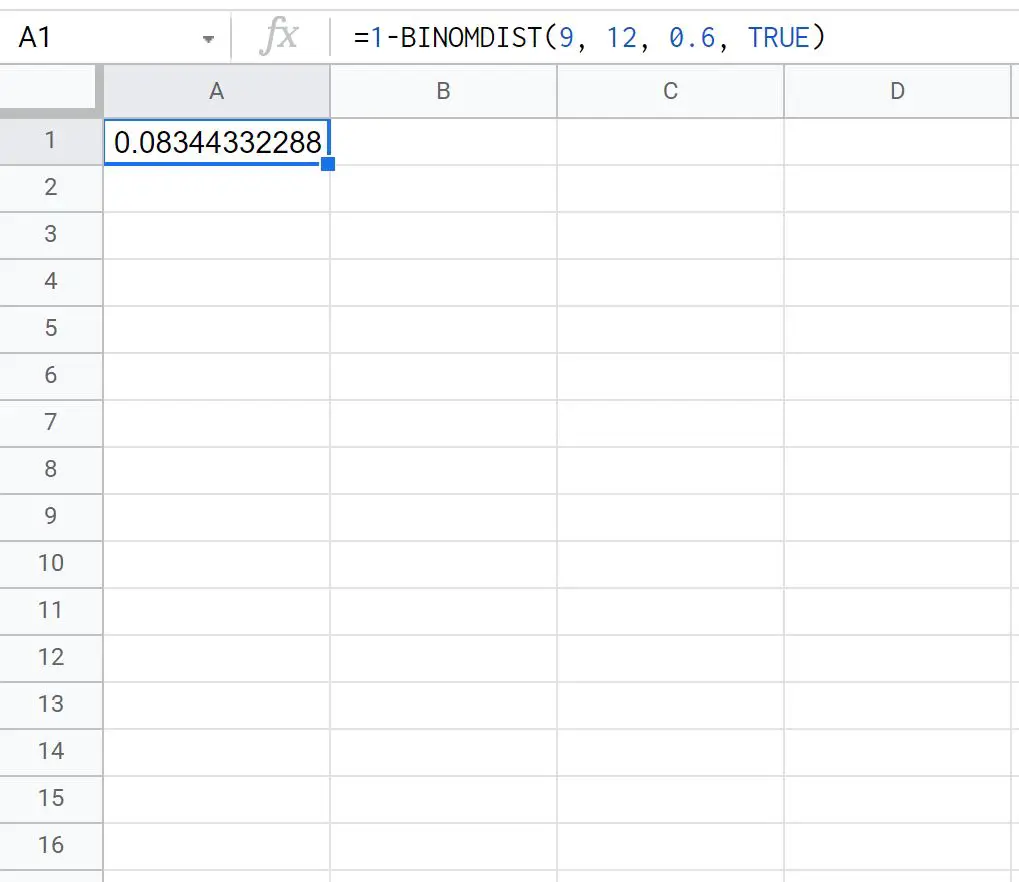
Die Wahrscheinlichkeit, dass Ty mindestens 10 von 12 Freiwurfversuchen macht, beträgt 0,0834 .
Bonus : Sie können den Binomialverteilungsrechner verwenden, um Binomialwahrscheinlichkeiten für alle Werte von n , k und p automatisch zu berechnen.
Zusätzliche Ressourcen
Die folgenden Tutorials bieten zusätzliche Informationen zur Binomialverteilung:
Eine Einführung in die Binomialverteilung
Die drei Hypothesen der Binomialverteilung
5 konkrete Beispiele der Binomialverteilung
Über den Autor
Dr. Benjamin Anderson
Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen