So verwenden sie die binomialverteilung in python

Die Binomialverteilung ist eine der am häufigsten verwendeten Verteilungen in der Statistik. Sie beschreibt die Wahrscheinlichkeit, in n Binomialexperimenten k Erfolge zu erzielen.

Wenn eine Zufallsvariable X einer Binomialverteilung folgt, kann die Erfolgswahrscheinlichkeit von X = k mit der folgenden Formel ermittelt werden:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

Gold:

• n: Anzahl der Versuche
• k: Anzahl der Erfolge
• p: Erfolgswahrscheinlichkeit bei einem bestimmten Versuch
• _n C _k : die Anzahl der Möglichkeiten, in n Versuchen k Erfolge zu erzielen

In diesem Tutorial wird erklärt, wie Sie die Binomialverteilung in Python verwenden.

So generieren Sie eine Binomialverteilung

Mit der Funktion random.binomial der Numpy-Bibliothek können Sie ein Wertearray generieren, das einer Binomialverteilung folgt:

 from numpy import random

#generate an array of 10 values that follows a binomial distribution
random.binomial(n=10, p=.25, size=10)

array([5, 2, 1, 3, 3, 3, 2, 2, 1, 4])

Jede Zahl in der resultierenden Tabelle stellt die Anzahl der „Erfolge“ dar, die im Verlauf von 10 Versuchen erzielt wurden, wobei die Erfolgswahrscheinlichkeit in einem bestimmten Versuch 0,25 betrug.

So berechnen Sie Wahrscheinlichkeiten mithilfe einer Binomialverteilung

Sie können Fragen zur Binomialwahrscheinlichkeit auch mit der Binomfunktion der Scipy-Bibliothek beantworten.

Frage 1: Nathan macht 60 % seiner Freiwurfversuche. Wenn er 12 Freiwürfe macht, wie groß ist dann die Wahrscheinlichkeit, dass er genau 10 macht?

 from scipy.stats import binom

#calculate binomial probability
binom.pmf(k= 10 , n= 12 , p= 0.6 )

0.0639

Die Wahrscheinlichkeit, dass Nathan genau 10 Freiwürfe macht, beträgt 0,0639 .

Frage 2: Marty wirft fünfmal eine faire Münze. Wie groß ist die Wahrscheinlichkeit, dass die Münze zweimal oder weniger „Kopf“ erscheint?

 from scipy.stats import binom

#calculate binomial probability
binom.cdf(k= 2 , n= 5 , p= 0.5 )

0.5

Die Wahrscheinlichkeit, dass die Münze zweimal oder weniger „Kopf“ zeigt, beträgt 0,5 .

Frage 3: Wir wissen, dass 70 % der Menschen ein bestimmtes Gesetz unterstützen. Wenn 10 Personen zufällig ausgewählt werden, wie groß ist die Wahrscheinlichkeit, dass zwischen 4 und 6 von ihnen das Gesetz unterstützen?

 from scipy.stats import binom

#calculate binomial probability
binom.cdf(k= 6 , n= 10 , p= 0.7 ) - binom.cdf(k= 3 , n= 10 , p= 0.7 )

0.3398

Die Wahrscheinlichkeit, dass zwischen 4 und 6 zufällig ausgewählte Personen das Gesetz unterstützen, beträgt 0,3398 .

So visualisieren Sie eine Binomialverteilung

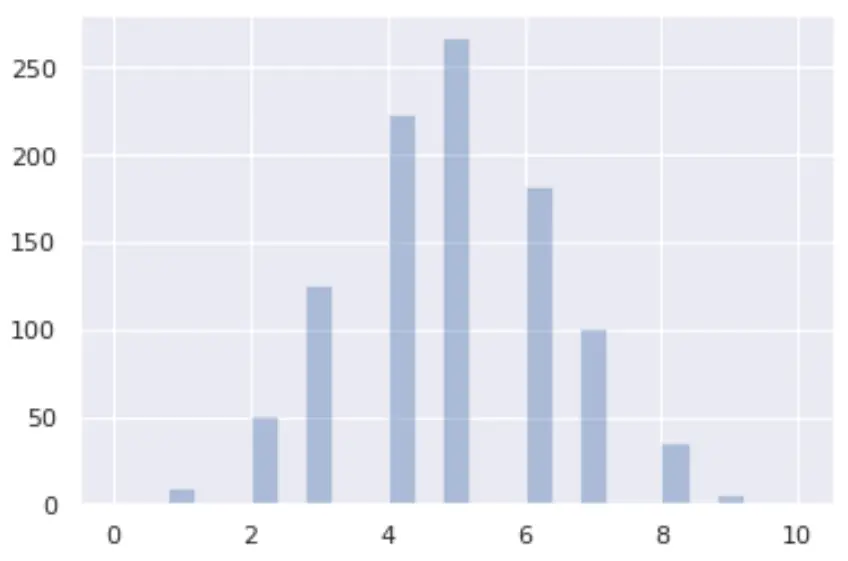
Sie können eine Binomialverteilung in Python mit den Bibliotheken seaborn und matplotlib visualisieren:

 from numpy import random
import matplotlib.pyplot as plt
import seaborn as sns

x = random.binomial(n= 10 , p= 0.5 , size= 1000 )

sns.distplot(x, hist= True , kde= False )

plt.show()

Tee