Die form einer binomialverteilung verstehen

DieBinomialverteilung beschreibt die Wahrscheinlichkeit, in n Binomialexperimenten k Erfolge zu erzielen.

Wenn eine Zufallsvariable X einer Binomialverteilung folgt, kann die Erfolgswahrscheinlichkeit von X = k mit der folgenden Formel ermittelt werden:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

Gold:

• n: Anzahl der Versuche
• k: Anzahl der Erfolge
• p: Erfolgswahrscheinlichkeit bei einem bestimmten Versuch
• _n C _k : die Anzahl der Möglichkeiten, in n Versuchen k Erfolge zu erzielen

Die binomiale Wahrscheinlichkeitsverteilung neigt dazu, glockenförmig zu sein, wenn eine oder mehrere der folgenden beiden Bedingungen eintritt:

1. Die Stichprobengröße (n) ist groß.

2. Die Erfolgswahrscheinlichkeit für einen bestimmten Versuch (p) liegt nahe bei 0,5.

Allerdings neigt die binomiale Wahrscheinlichkeitsverteilung dazu, verzerrt zu sein, wenn keine dieser Bedingungen eintritt. Um dies zu veranschaulichen, betrachten Sie die folgenden Beispiele:

Beispiel 1: Die Stichprobengröße (n) ist groß

Das folgende Diagramm zeigt die Wahrscheinlichkeitsverteilung für n = 200 und p = 0,5 .

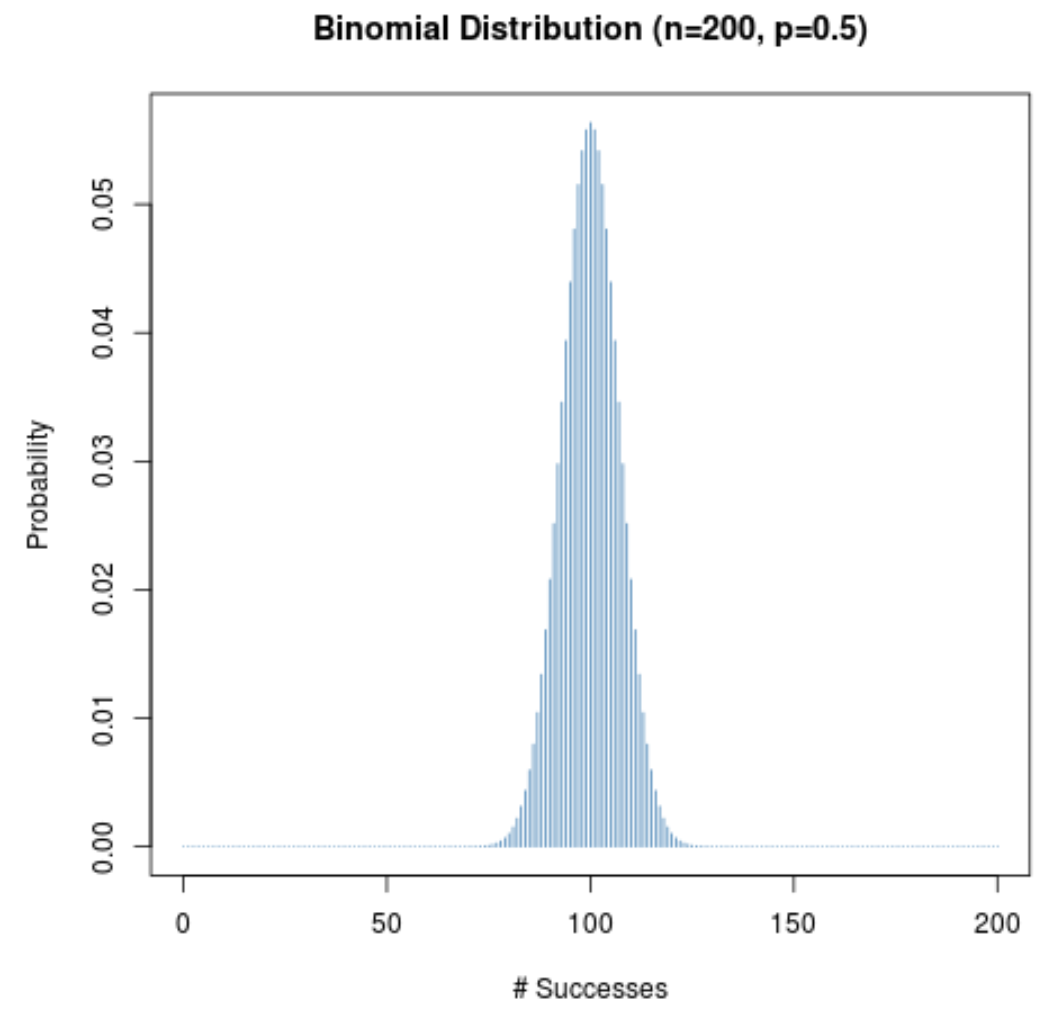
Die x-Achse zeigt die Anzahl der Erfolge über 200 Versuche und die y-Achse zeigt die Wahrscheinlichkeit an, mit der diese Anzahl an Erfolgen auftritt.

Da (1) die Stichprobengröße groß ist und (2) die Erfolgswahrscheinlichkeit für einen bestimmten Versuch nahe bei 0,5 liegt, ist die Wahrscheinlichkeitsverteilung glockenförmig.

Selbst wenn die Erfolgswahrscheinlichkeit für einen bestimmten Versuch (p) nicht nahe bei 0,5 liegt, bleibt die Wahrscheinlichkeitsverteilung glockenförmig, solange die Stichprobengröße (n) groß ist. Um dies zu veranschaulichen, betrachten Sie die folgenden zwei Szenarien, wenn p = 0,2 und p = 0,8.

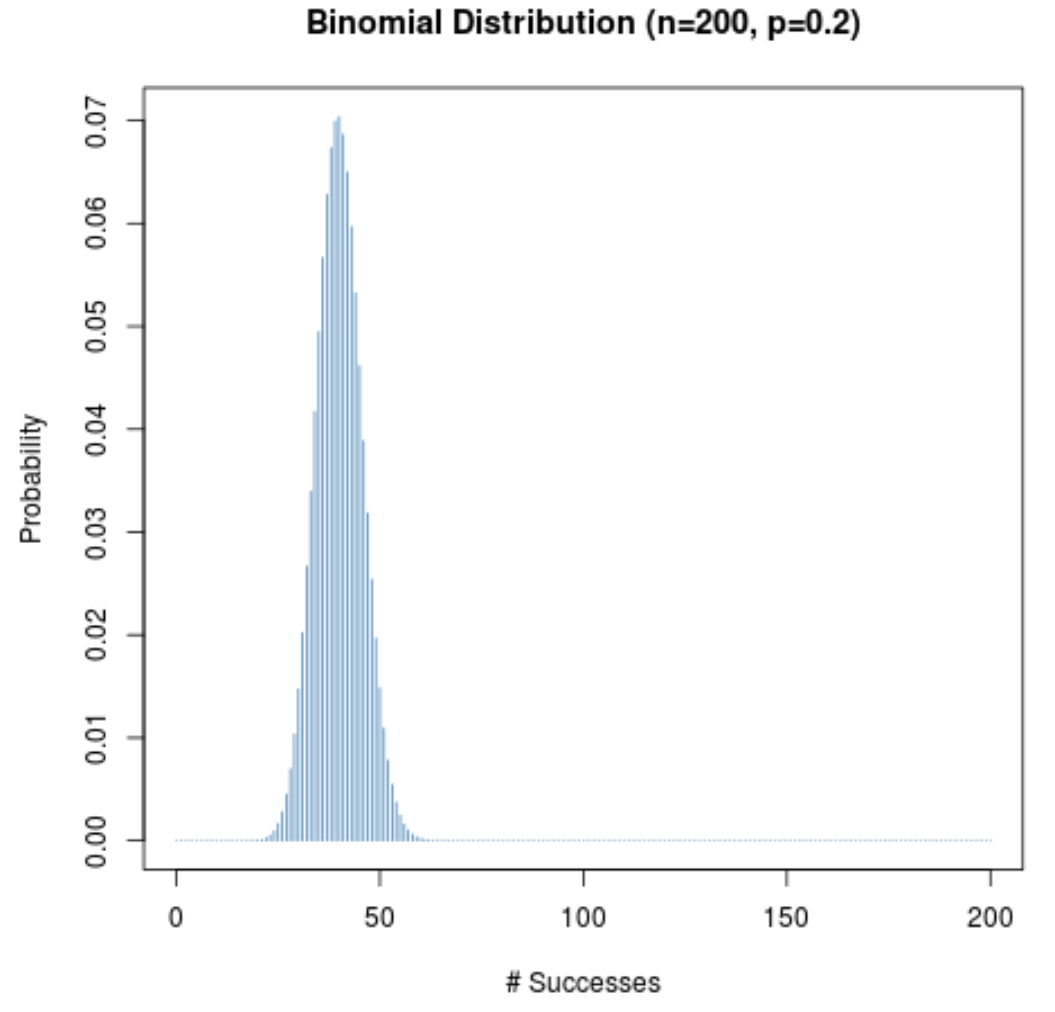
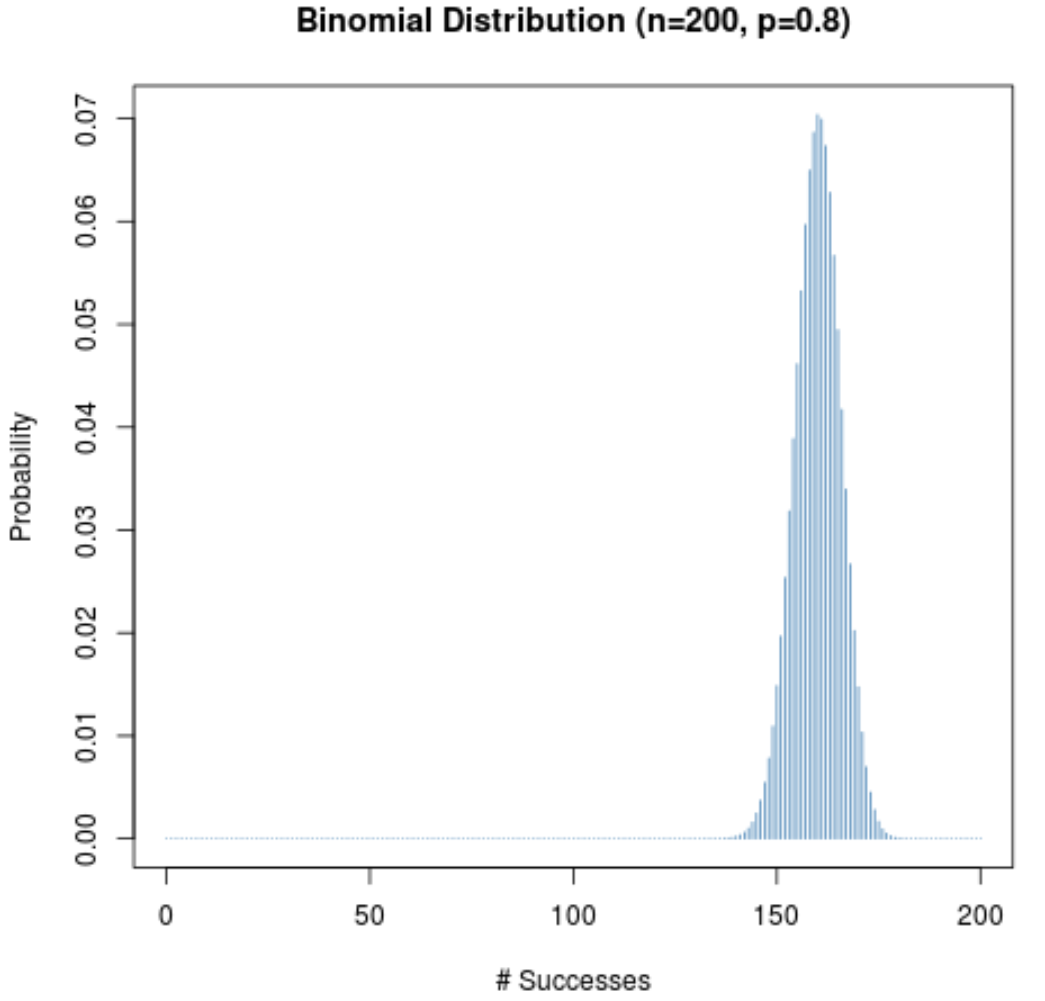
Beachten Sie, dass die Wahrscheinlichkeitsverteilung in beiden Szenarien glockenförmig ist.

Beispiel 2: Die Erfolgswahrscheinlichkeit (p) liegt nahe bei 0,5

Das folgende Diagramm zeigt die Wahrscheinlichkeitsverteilung, wenn n = 10 und p = 0,4 .

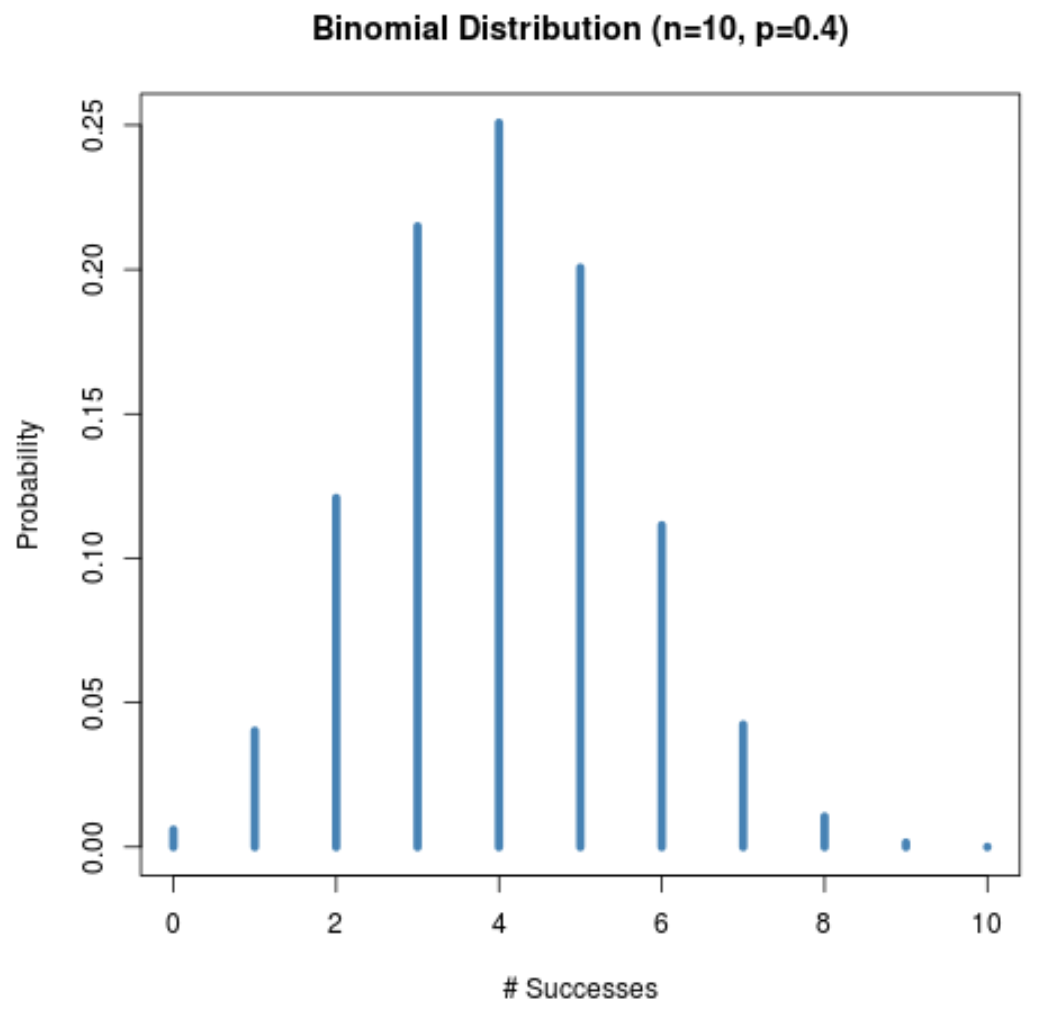
Obwohl die Stichprobengröße (n = 10) klein ist, bleibt die Wahrscheinlichkeitsverteilung glockenförmig, da die Erfolgswahrscheinlichkeit für einen bestimmten Versuch (p = 0,4) nahe bei 0,5 liegt.

Beispiel 3: Schiefe Binomialverteilungen

Wenn weder (1) die Stichprobengröße groß ist noch (2) die Erfolgswahrscheinlichkeit eines bestimmten Versuchs nahe bei 0,5 liegt, ist die binomiale Wahrscheinlichkeitsverteilung nach links oder rechts verzerrt.

Das folgende Diagramm zeigt beispielsweise die Wahrscheinlichkeitsverteilung, wenn n = 20 und p = 0,1 .

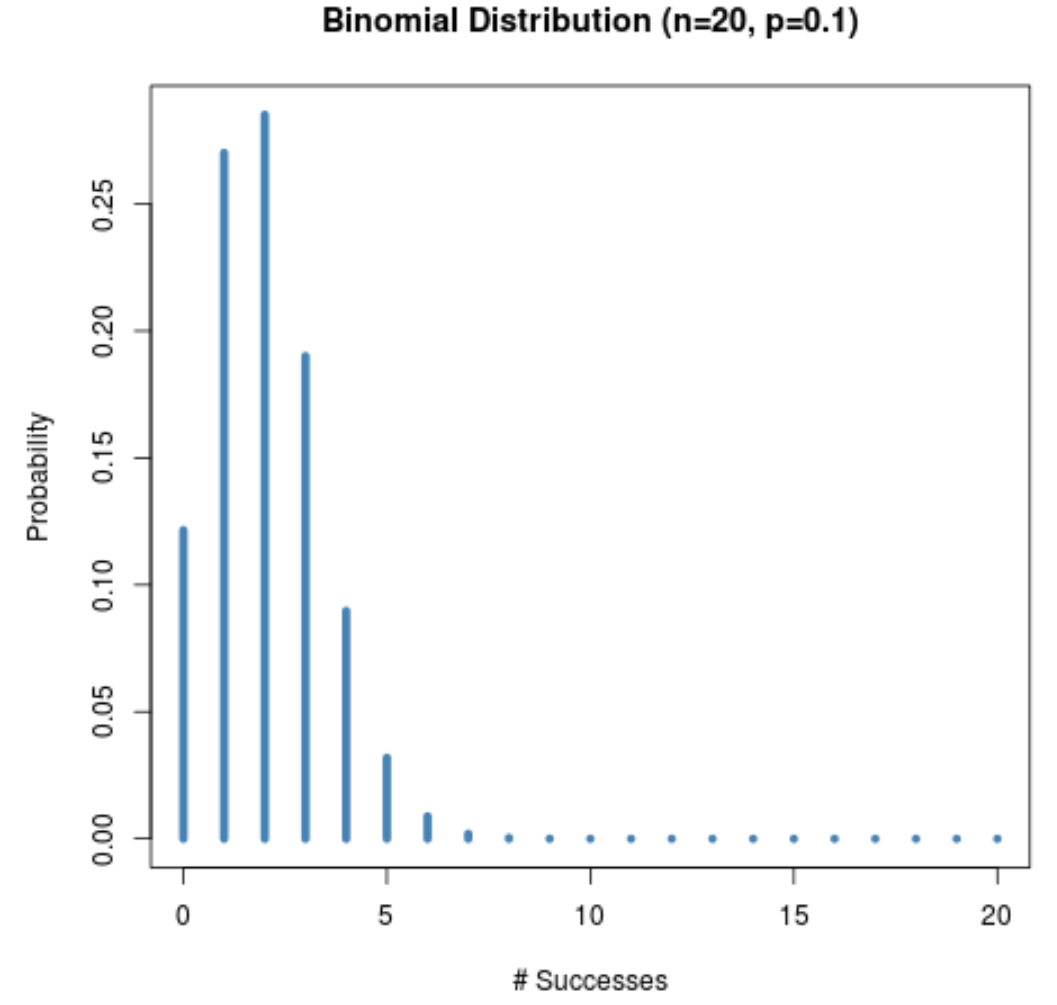
Beachten Sie, dass die Verteilung rechtsschief ist.

Und die folgende Grafik zeigt die Wahrscheinlichkeitsverteilung, wenn n = 20 und p = 0,9 .

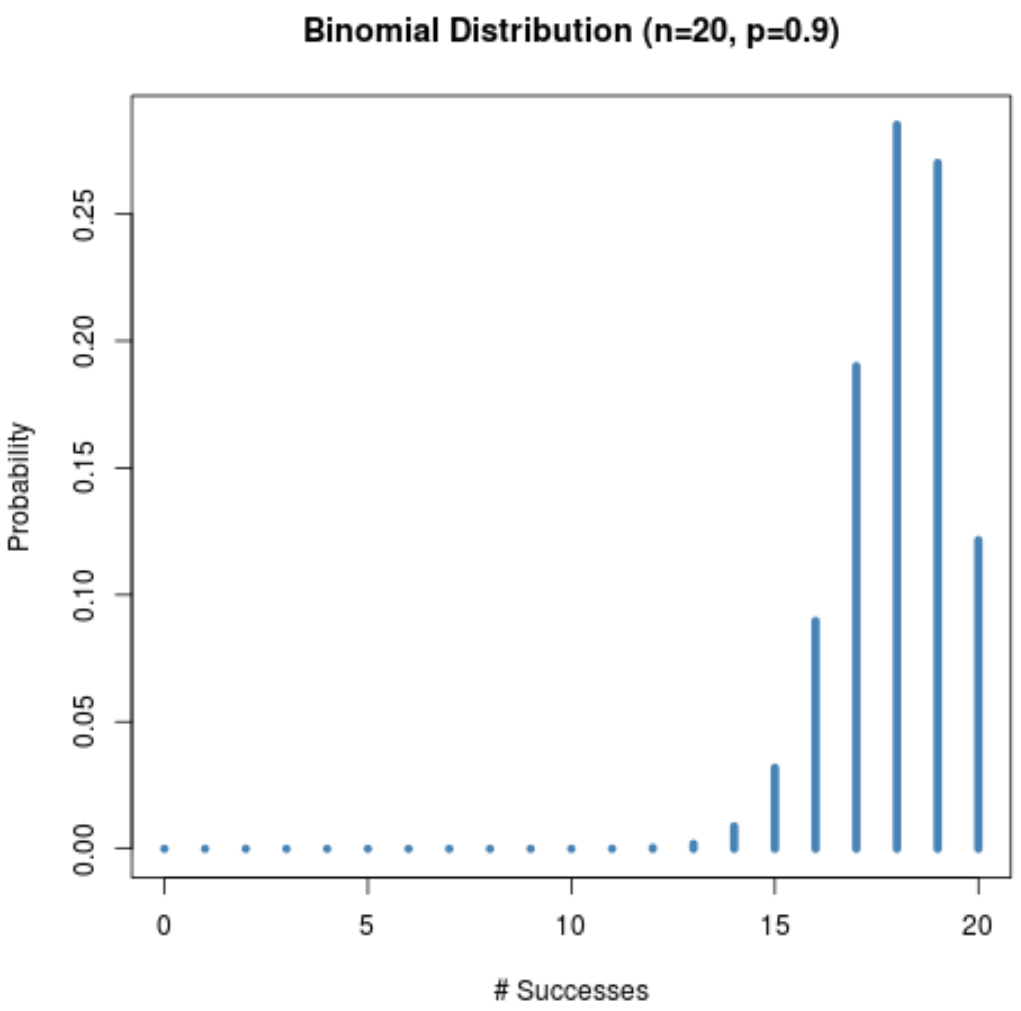
Beachten Sie, dass die Verteilung nach links schief ist.

Endnoten

Jedes der Diagramme in diesem Artikel wurde mit der statistischen Programmiersprache R erstellt. Erfahren Sie in diesem Tutorial , wie Sie Ihre eigenen binomialen Wahrscheinlichkeitsverteilungen in R darstellen.