Binompdf vs. binomcdf: der unterschied (plus beispiele)
Die Binomialverteilung ist eine der am häufigsten verwendeten Verteilungen in allen Statistiken.
Auf einem TI-84-Rechner können Sie zwei Funktionen verwenden, um Wahrscheinlichkeiten im Zusammenhang mit der Binomialverteilung zu ermitteln:
- binompdf(n, p, x) : ermittelt die Wahrscheinlichkeit, dass im Verlauf von n Versuchen genau x Erfolge auftreten, wobei die Erfolgswahrscheinlichkeit bei einem bestimmten Versuch gleich p ist.
- binomcdf(n, p, x) : ermittelt die Wahrscheinlichkeit, dass in n Versuchen x oder weniger Erfolge auftreten, wobei die Erfolgswahrscheinlichkeit bei einem bestimmten Versuch gleich p ist.
Sie können auf jede dieser Funktionen auf einem TI-84-Rechner zugreifen, indem Sie 2nd und dann VARS drücken. Dadurch gelangen Sie zu einem DISTR- Bildschirm, in dem Sie dann binompdf() und binomcdf() verwenden können:
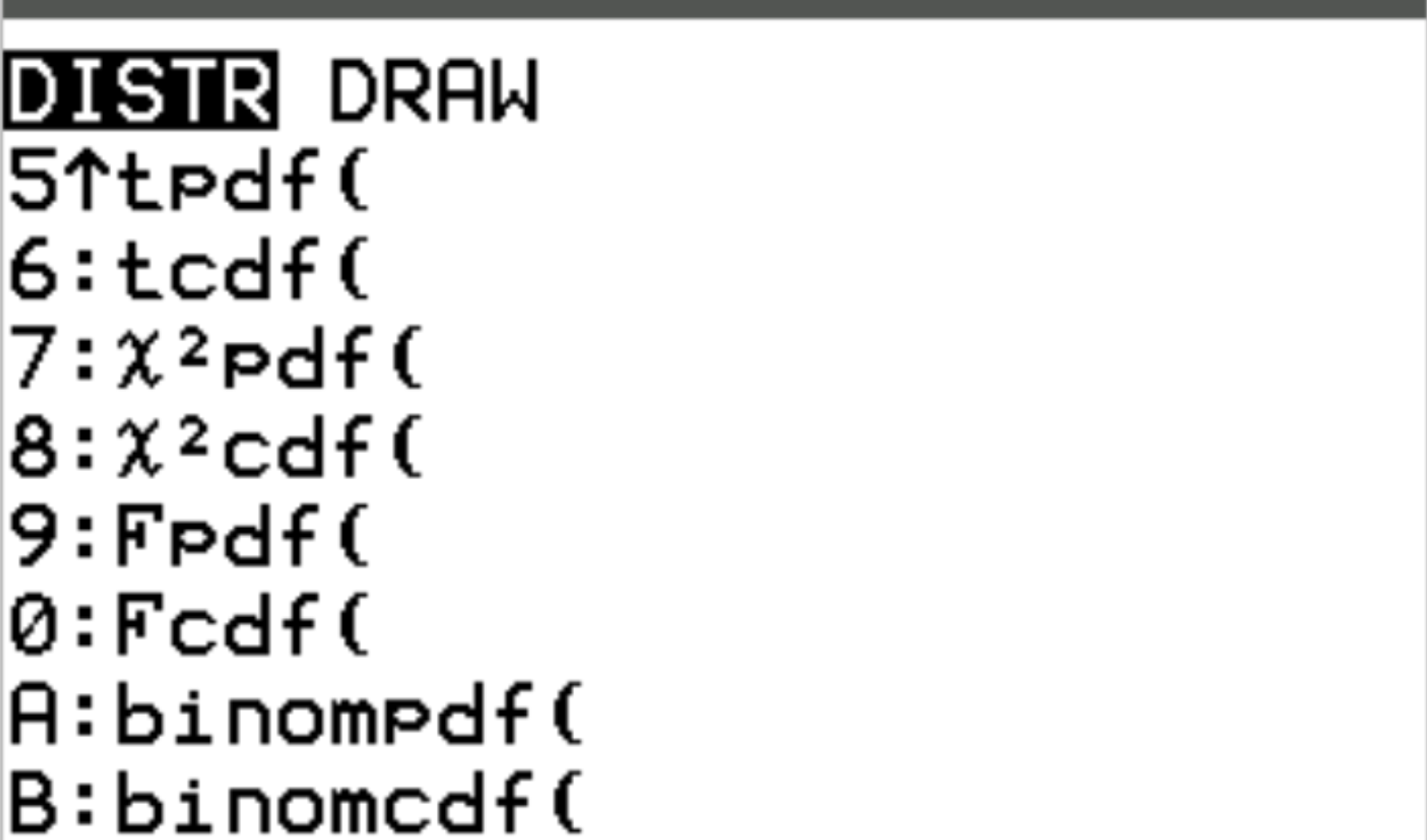
Die folgenden Beispiele zeigen, wie Sie jede dieser Funktionen in der Praxis nutzen können.
Beispiele: Verwendung von Binompdf()
Die folgenden Beispiele zeigen, wie die Funktion binompdf() verwendet wird.
Beispiel 1: Freiwurfversuche
Jessica macht 80 % ihrer Freiwurfversuche. Wenn sie 10 Freiwürfe macht, wie groß ist dann die Wahrscheinlichkeit, dass sie genau 7 macht?
Um diese Frage zu beantworten, können wir die folgende Formel eingeben:
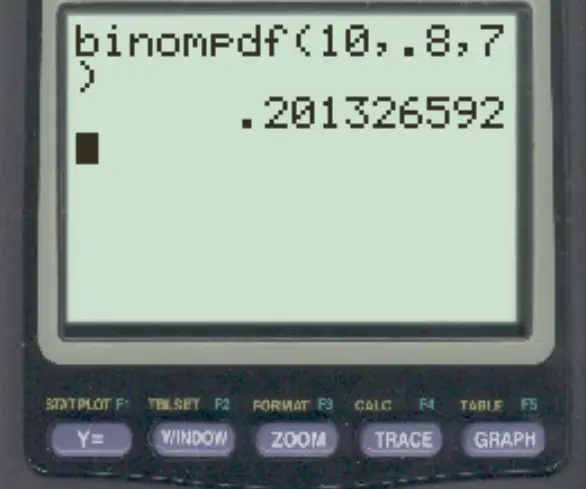
Die Wahrscheinlichkeit, dass sie genau 7 bekommt, beträgt 0,2013 .
Beispiel 2: Betrügerische Transaktionen
Eine Bank weiß, dass 3 % aller Transaktionen betrügerisch sind. Wenn an einem Tag 20 Transaktionen stattfinden, wie groß ist dann die Wahrscheinlichkeit, dass genau 2 betrügerisch sind?
Um diese Frage zu beantworten, können wir die folgende Formel eingeben:
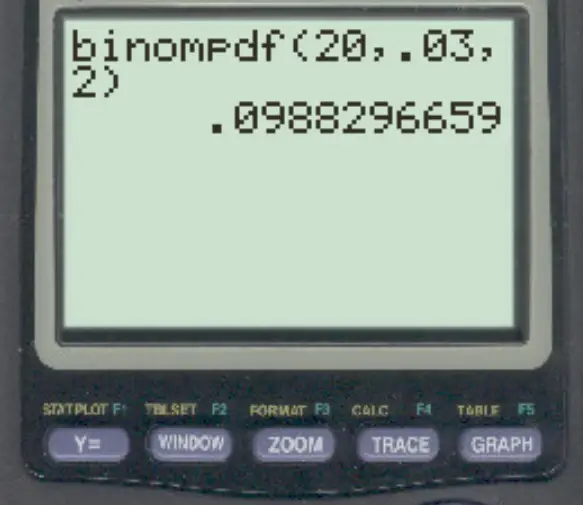
Die Wahrscheinlichkeit, dass genau 2 Transaktionen betrügerisch sind, beträgt 0,0988 .
Beispiele: Verwendung von Binomcdf()
Die folgenden Beispiele zeigen, wie die Funktion binomcdf() verwendet wird.
Beispiel 1: Freiwurfversuche
Jessica macht 50 % ihrer Freiwurfversuche. Wenn sie 10 Freiwürfe macht, wie hoch ist dann die Wahrscheinlichkeit, dass sie 7 oder weniger macht?
Um diese Frage zu beantworten, können wir die folgende Formel eingeben:
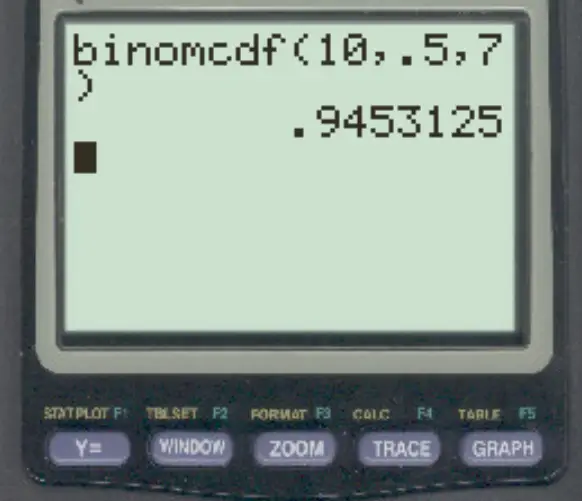
Die Wahrscheinlichkeit, dass sie 7 oder weniger Freiwürfe macht, beträgt 0,9453 .
Beispiel 2: Betrügerische Transaktionen
Eine Bank weiß, dass 3 % aller Transaktionen betrügerisch sind. Wie hoch ist die Wahrscheinlichkeit, dass mehr als zwei Transaktionen betrügerisch sind, wenn an einem Tag 20 Transaktionen stattfinden?
Um diese Frage zu beantworten, können wir die folgende Formel eingeben:
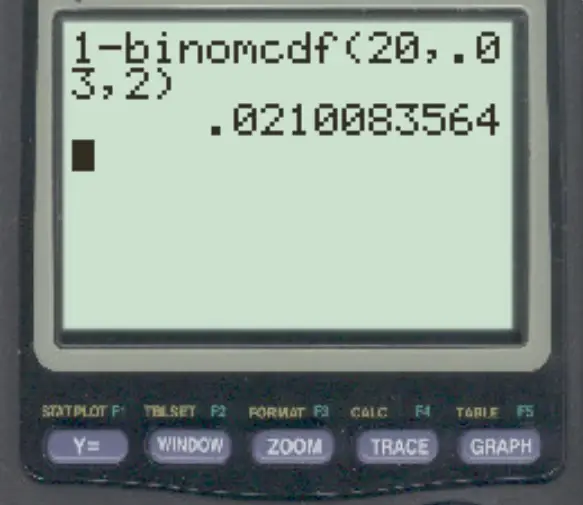
Die Wahrscheinlichkeit, dass mehr als 2 Transaktionen betrügerisch sind, beträgt 0,021 .
Zusätzliche Ressourcen
Binomialverteilungsrechner
So führen Sie einen Binomialtest in Excel durch