So führen sie eine bivariate analyse in python durch: mit beispielen

Der Begriff bivariate Analyse bezieht sich auf die Analyse zweier Variablen. Sie können sich das merken, denn das Präfix „bi“ bedeutet „zwei“.

Das Ziel der bivariaten Analyse besteht darin, die Beziehung zwischen zwei Variablen zu verstehen

Es gibt drei gängige Methoden zur Durchführung einer bivariaten Analyse:

1. Punktwolken

2. Korrelationskoeffizienten

3. Einfache lineare Regression

Das folgende Beispiel zeigt, wie jede dieser Arten der bivariaten Analyse in Python mithilfe des folgenden Pandas-DataFrames durchgeführt wird, der Informationen zu zwei Variablen enthält: (1) Stunden, die mit dem Lernen verbracht wurden, und (2) Prüfungsergebnis von 20 verschiedenen Studenten:

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' hours ': [1, 1, 1, 2, 2, 2, 3, 3, 3, 3,
                             3, 4, 4, 5, 5, 6, 6, 6, 7, 8],
                   ' score ': [75, 66, 68, 74, 78, 72, 85, 82, 90, 82,
                             80, 88, 85, 90, 92, 94, 94, 88, 91, 96]})

#view first five rows of DataFrame
df. head ()

	hours score
0 1 75
1 1 66
2 1 68
3 2 74
4 2 78

1. Punktwolken

Wir können die folgende Syntax verwenden, um ein Streudiagramm der gelernten Stunden im Vergleich zu den Prüfungsergebnissen zu erstellen:

 import matplotlib. pyplot as plt

#create scatterplot of hours vs. score
plt. scatter (df. hours , df. score )
plt. title (' Hours Studied vs. Exam Score ')
plt. xlabel (' Hours Studied ')
plt. ylabel (' Exam Score ')

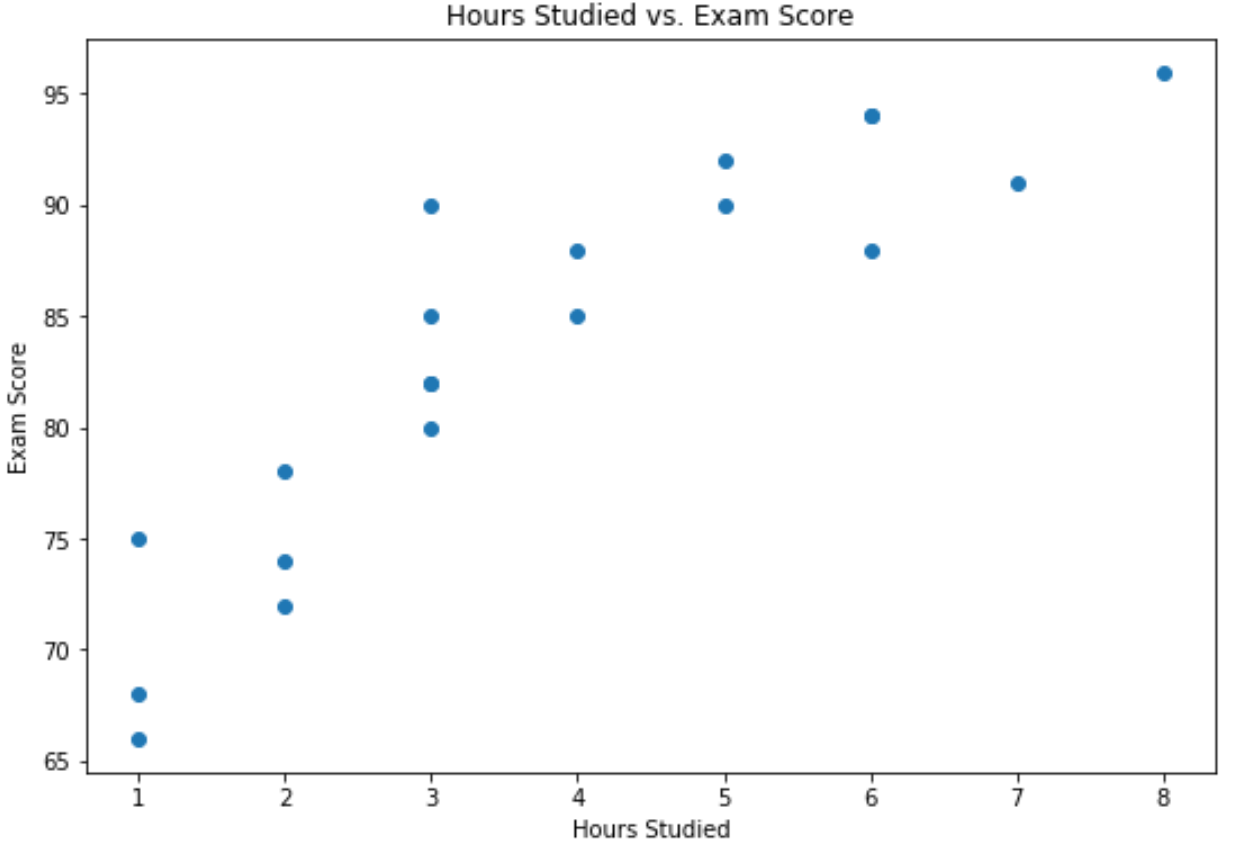
Die x-Achse zeigt die gelernten Stunden und die y-Achse die bei der Prüfung erzielte Note.

Die Grafik zeigt, dass ein positiver Zusammenhang zwischen den beiden Variablen besteht: Mit zunehmender Anzahl der Lernstunden steigen tendenziell auch die Prüfungsergebnisse.

2. Korrelationskoeffizienten

Ein Pearson-Korrelationskoeffizient ist eine Möglichkeit, die lineare Beziehung zwischen zwei Variablen zu quantifizieren.

Wir können die Funktion corr() in Pandas verwenden, um eine Korrelationsmatrix zu erstellen:

 #create correlation matrix
df. corr ()

	hours score
hours 1.000000 0.891306
score 0.891306 1.000000

Der Korrelationskoeffizient beträgt 0,891 . Dies weist auf eine starke positive Korrelation zwischen den gelernten Stunden und der Prüfungsnote hin.

3. Einfache lineare Regression

Die einfache lineare Regression ist eine statistische Methode, mit der wir die Beziehung zwischen zwei Variablen quantifizieren können.

Wir können die Funktion OLS() aus dem statsmodels-Paket verwenden, um schnell ein einfaches lineares Regressionsmodell für die untersuchten Stunden und die erhaltenen Prüfungsergebnisse anzupassen:

 import statsmodels. api as sm

#define response variable
y = df[' score ']

#define explanatory variable
x = df[[' hours ']]

#add constant to predictor variables
x = sm. add_constant (x)

#fit linear regression model
model = sm. OLS (y,x). fit ()

#view model summary
print ( model.summary ())

                            OLS Regression Results                            
==================================================== ============================
Dept. Variable: R-squared score: 0.794
Model: OLS Adj. R-squared: 0.783
Method: Least Squares F-statistic: 69.56
Date: Mon, 22 Nov 2021 Prob (F-statistic): 1.35e-07
Time: 16:15:52 Log-Likelihood: -55,886
No. Observations: 20 AIC: 115.8
Df Residuals: 18 BIC: 117.8
Model: 1                                         
Covariance Type: non-robust                                         
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
const 69.0734 1.965 35.149 0.000 64.945 73.202
hours 3.8471 0.461 8.340 0.000 2.878 4.816
==================================================== ============================
Omnibus: 0.171 Durbin-Watson: 1.404
Prob(Omnibus): 0.918 Jarque-Bera (JB): 0.177
Skew: 0.165 Prob(JB): 0.915
Kurtosis: 2.679 Cond. No. 9.37
==================================================== ============================

Die angepasste Regressionsgleichung lautet:

Prüfungsergebnis = 69,0734 + 3,8471*(Studienstunden)

Dies zeigt uns, dass jede zusätzliche gelernte Stunde mit einer durchschnittlichen Steigerung der Prüfungspunktzahl um 3,8471 verbunden ist.

Wir können die angepasste Regressionsgleichung auch verwenden, um die Punktzahl vorherzusagen, die ein Schüler basierend auf der Gesamtzahl der gelernten Stunden erhalten wird.

Beispielsweise sollte ein Student, der 3 Stunden lernt, eine Punktzahl von 81,6147 erreichen:

• Prüfungsergebnis = 69,0734 + 3,8471*(Studienstunden)
• Prüfungsergebnis = 69,0734 + 3,8471*(3)
• Prüfungsergebnis = 81,6147

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zur bivariaten Analyse:

Eine Einführung in die bivariate Analyse
5 Beispiele für bivariate Daten im wirklichen Leben
Eine Einführung in die einfache lineare Regression
Eine Einführung in den Pearson-Korrelationskoeffizienten