So führen sie eine bivariate analyse in r durch (mit beispielen)

Der Begriff bivariate Analyse bezieht sich auf die Analyse zweier Variablen. Sie können sich das merken, denn das Präfix „bi“ bedeutet „zwei“.

Das Ziel der bivariaten Analyse besteht darin, die Beziehung zwischen zwei Variablen zu verstehen

Es gibt drei gängige Methoden zur Durchführung einer bivariaten Analyse:

1. Punktwolken

2. Korrelationskoeffizienten

3. Einfache lineare Regression

Das folgende Beispiel zeigt, wie jede dieser Arten der bivariaten Analyse unter Verwendung des folgenden Datensatzes durchgeführt wird, der Informationen zu zwei Variablen enthält: (1) Stunden, die mit dem Lernen verbracht wurden, und (2) Testergebnisse, die von 20 verschiedenen Studenten erzielt wurden:

 #create data frame
df <- data. frame (hours=c(1, 1, 1, 2, 2, 2, 3, 3, 3, 3,
                         3, 4, 4, 5, 5, 6, 6, 6, 7, 8),
                 score=c(75, 66, 68, 74, 78, 72, 85, 82, 90, 82,
                         80, 88, 85, 90, 92, 94, 94, 88, 91, 96))

#view first six rows of data frame
head(df)

  hours score
1 1 75
2 1 66
3 1 68
4 2 74
5 2 78
6 2 72

1. Punktwolken

Wir können die folgende Syntax verwenden, um ein Streudiagramm der gelernten Stunden im Vergleich zur Prüfungsnote in R zu erstellen:

 #create scatterplot of hours studied vs. exam score
plot(df$hours, df$score, pch= 16 , col=' steelblue ',
     main=' Hours Studied vs. Exam Score ',
     xlab=' Hours Studied ', ylab=' Exam Score ')

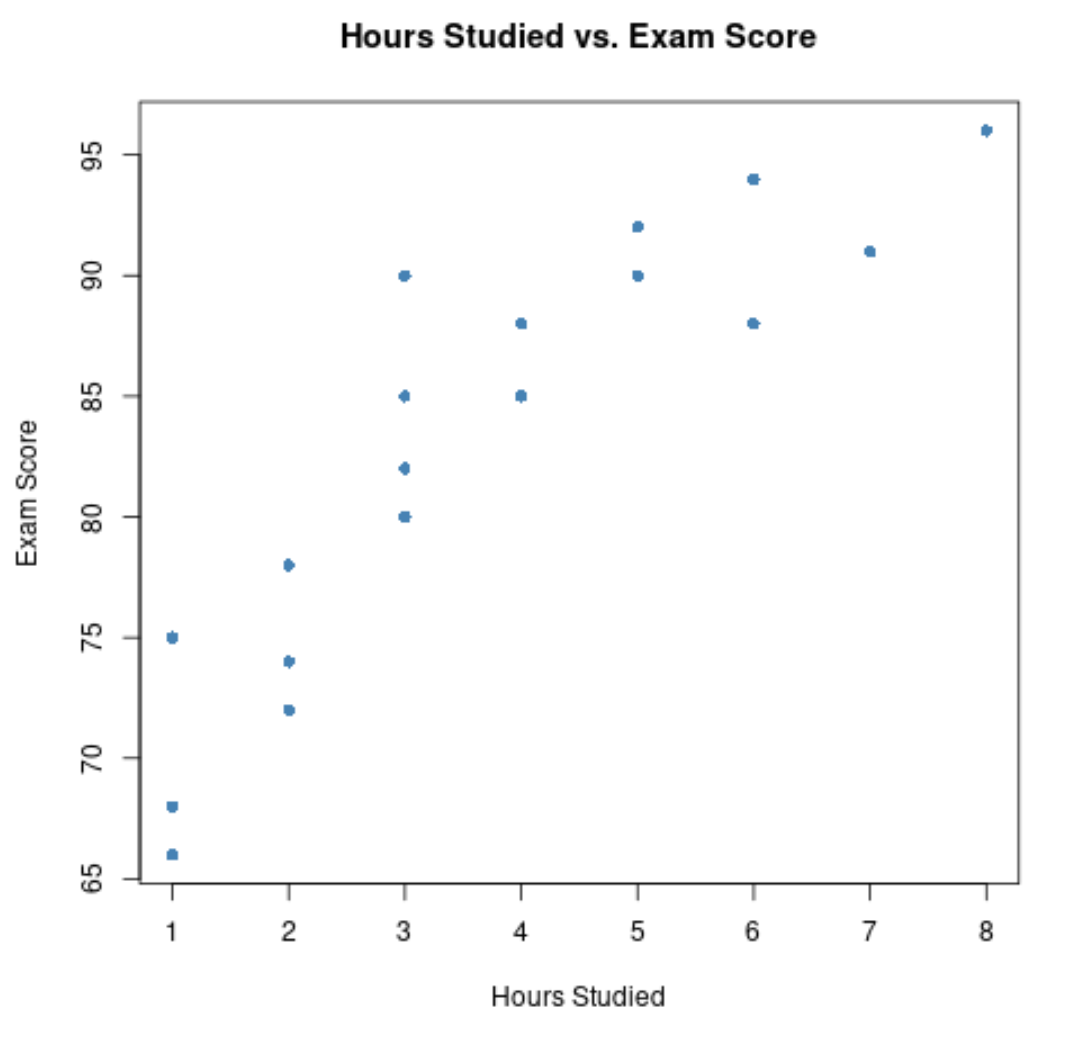
Die x-Achse zeigt die gelernten Stunden und die y-Achse die bei der Prüfung erzielte Note.

Die Grafik zeigt, dass ein positiver Zusammenhang zwischen den beiden Variablen besteht: Mit zunehmender Anzahl der Lernstunden steigen tendenziell auch die Prüfungsergebnisse.

2. Korrelationskoeffizienten

Ein Pearson-Korrelationskoeffizient ist eine Möglichkeit, die lineare Beziehung zwischen zwei Variablen zu quantifizieren.

Wir können die Funktion cor() in R verwenden, um den Pearson-Korrelationskoeffizienten zwischen zwei Variablen zu berechnen:

 #calculate correlation between hours studied and exam score received
cor(df$hours, df$score)

[1] 0.891306

Der Korrelationskoeffizient beträgt 0,891 .

Dieser Wert liegt nahe bei 1, was auf eine starke positive Korrelation zwischen den gelernten Stunden und der Prüfungsnote hinweist.

3. Einfache lineare Regression

Die einfache lineare Regression ist eine statistische Methode, mit der wir die Gleichung der Geraden finden können, die am besten zu einem Datensatz „passt“, um dann die genaue Beziehung zwischen zwei Variablen zu verstehen.

Wir können die Funktion lm() in R verwenden, um ein einfaches lineares Regressionsmodell für die untersuchten Stunden und die erhaltenen Prüfungsergebnisse anzupassen:

 #fit simple linear regression model
fit <- lm(score ~ hours, data=df)

#view summary of model
summary(fit)

Call:
lm(formula = score ~ hours, data = df)

Residuals:
   Min 1Q Median 3Q Max 
-6,920 -3,927 1,309 1,903 9,385 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 69.0734 1.9651 35.15 < 2nd-16 ***
hours 3.8471 0.4613 8.34 1.35e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 4.171 on 18 degrees of freedom
Multiple R-squared: 0.7944, Adjusted R-squared: 0.783 
F-statistic: 69.56 on 1 and 18 DF, p-value: 1.347e-07

Die angepasste Regressionsgleichung lautet:

Prüfungsergebnis = 69,0734 + 3,8471*(Studienstunden)

Dies zeigt uns, dass jede zusätzliche gelernte Stunde mit einer durchschnittlichen Steigerung der Prüfungspunktzahl um 3,8471 verbunden ist.

Wir können die angepasste Regressionsgleichung auch verwenden, um die Punktzahl vorherzusagen, die ein Schüler basierend auf der Gesamtzahl der gelernten Stunden erhalten wird.

Beispielsweise sollte ein Student, der 3 Stunden lernt, eine Punktzahl von 81,6147 erreichen:

• Prüfungsergebnis = 69,0734 + 3,8471*(Studienstunden)
• Prüfungsergebnis = 69,0734 + 3,8471*(3)
• Prüfungsergebnis = 81,6147

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zur bivariaten Analyse:

Eine Einführung in die bivariate Analyse
5 Beispiele für bivariate Daten im wirklichen Leben
Eine Einführung in die einfache lineare Regression