5 beispiele für bivariate daten im wirklichen leben

Unter bivariaten Daten versteht man einen Datensatz, der genau zwei Variablen enthält.

Diese Art von Daten taucht ständig in realen Situationen auf und wir verwenden normalerweise die folgenden Methoden, um diese Art von Daten zu analysieren:

• Punktwolken
• Korrelationskoeffizienten
• Einfache lineare Regression

Die folgenden Beispiele zeigen verschiedene Szenarien, in denen bivariate Daten im wirklichen Leben auftreten.

Beispiel 1: Geschäft

Unternehmen sammeln häufig bivariate Daten über die Gesamtausgaben für Werbung und den Gesamtumsatz.

Beispielsweise könnte ein Unternehmen die folgenden Daten für 12 aufeinanderfolgende Verkaufsquartale sammeln:

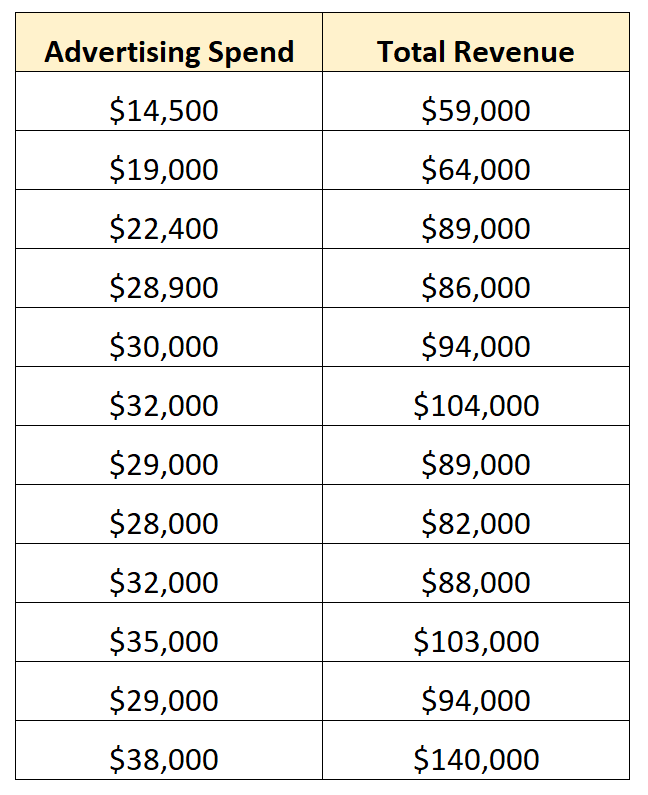
Dies ist ein Beispiel für bivariate Daten, da sie Informationen zu genau zwei Variablen enthalten: Werbeausgaben und Gesamtumsatz.

Das Unternehmen kann beschließen, ein einfaches lineares Regressionsmodell an diesen Datensatz anzupassen und das folgende angepasste Modell zu finden:

Gesamteinnahmen = 14.942,75 + 2,70* (Werbekosten)

Dies zeigt dem Unternehmen, dass sich der Gesamtumsatz für jeden zusätzlichen Dollar, der für Werbung ausgegeben wird, um durchschnittlich 2,70 Dollar erhöht.

Beispiel 2: Medizin

Medizinische Forscher sammeln häufig bivariate Daten, um die Beziehung zwischen gesundheitsbezogenen Variablen besser zu verstehen.

Beispielsweise könnte ein Forscher die folgenden Alters- und verbleibenden Herzfrequenzdaten von 15 Personen sammeln:

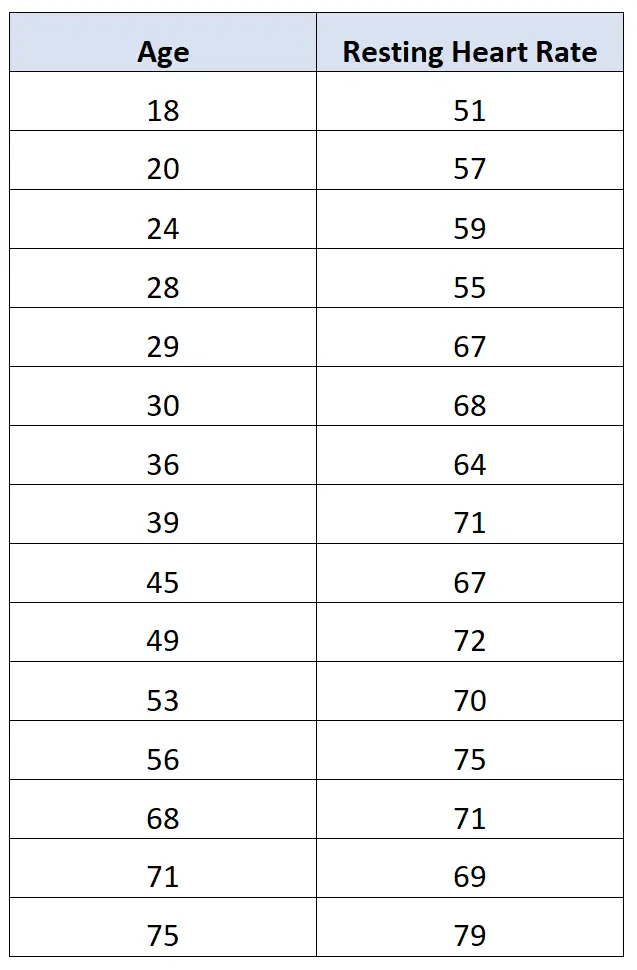
Der Forscher kann dann entscheiden, die Korrelation zwischen den beiden Variablen zu berechnen und einen Wert von 0,812 zu ermitteln.

Dies deutet darauf hin, dass zwischen den beiden Variablen eine starke positive Korrelation besteht. Das heißt, mit zunehmendem Alter steigt auch die verbleibende Herzfrequenz vorhersehbar an.

Verwandt: Was gilt als „starke“ Korrelation?

Beispiel 3: Akademiker

Forscher sammeln häufig bivariate Daten, um zu verstehen, welche Variablen die Leistung von Studenten beeinflussen.

Beispielsweise könnte ein Forscher Daten über die Anzahl der pro Woche gelernten Stunden und den entsprechenden Notendurchschnitt für Schüler einer bestimmten Klasse sammeln:

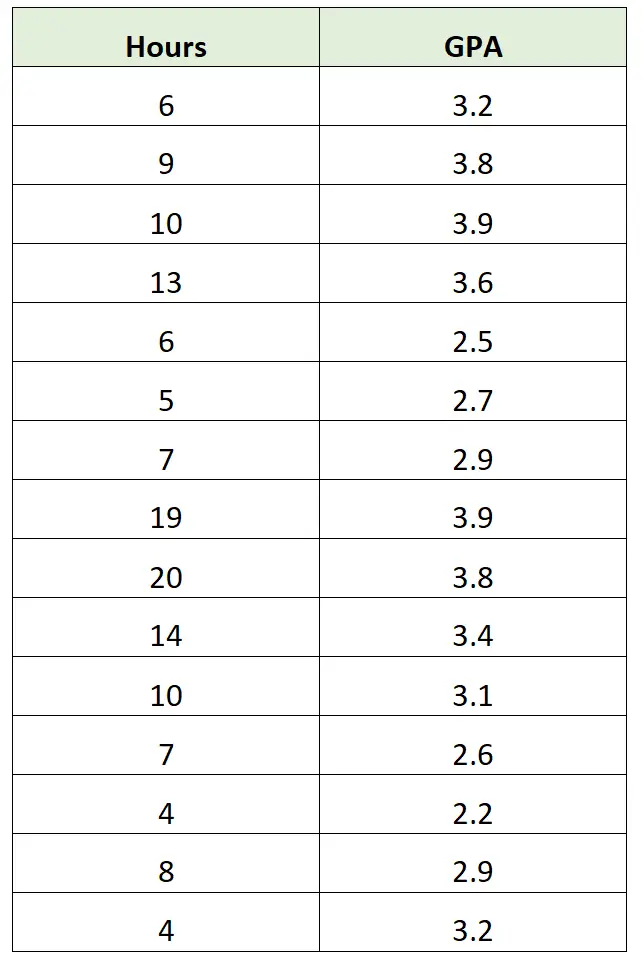
Anschließend kann sie ein einfaches Streudiagramm erstellen, um die Beziehung zwischen diesen beiden Variablen zu visualisieren:

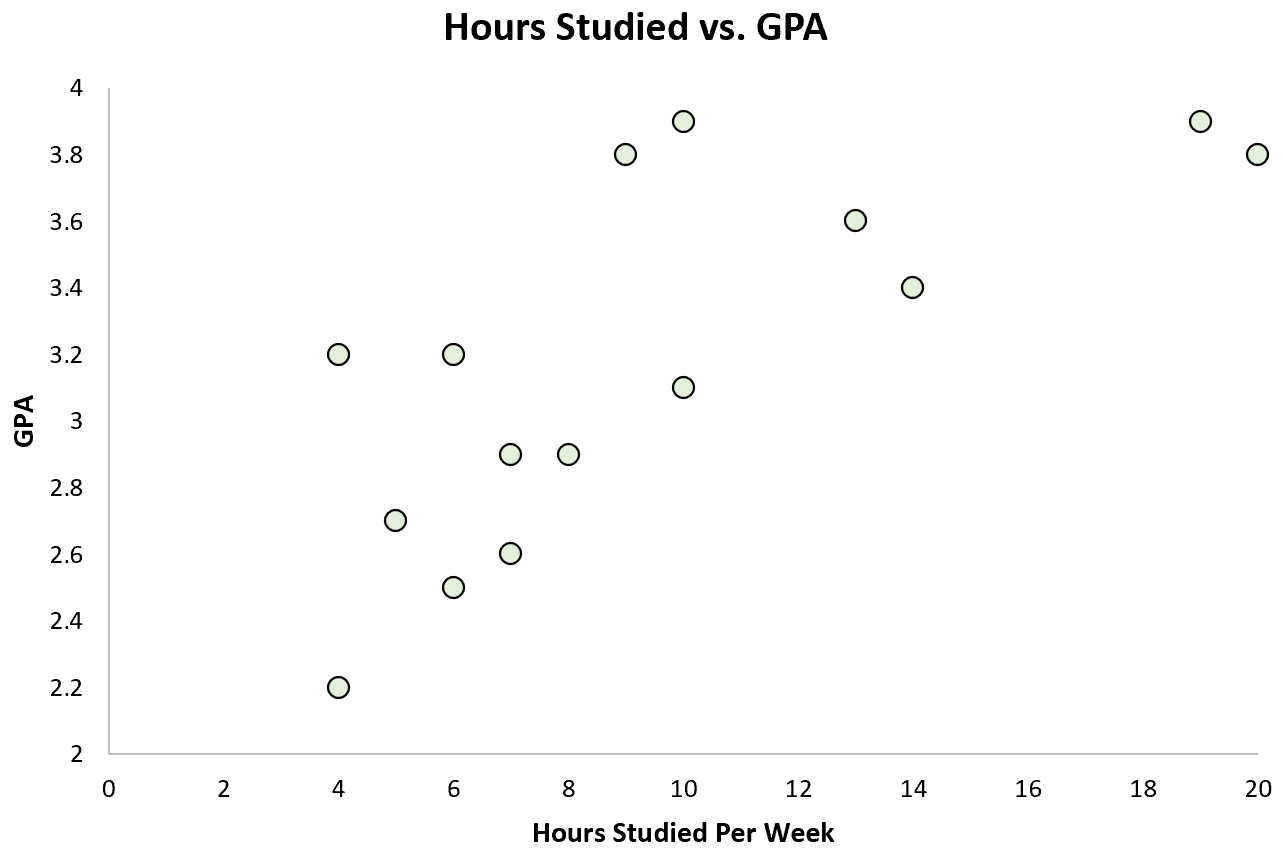
Es besteht eindeutig ein positiver Zusammenhang zwischen den beiden Variablen: Mit zunehmender Anzahl der pro Woche gelernten Stunden steigt tendenziell auch der Notendurchschnitt des Schülers.

Beispiel 4: Wirtschaft

Ökonomen sammeln häufig bivariate Daten, um die Beziehung zwischen zwei sozioökonomischen Variablen zu verstehen.

Beispielsweise könnte ein Wirtschaftswissenschaftler Daten über die Gesamtzahl der Schuljahre und das gesamte Jahreseinkommen von Einzelpersonen in einer bestimmten Stadt sammeln:

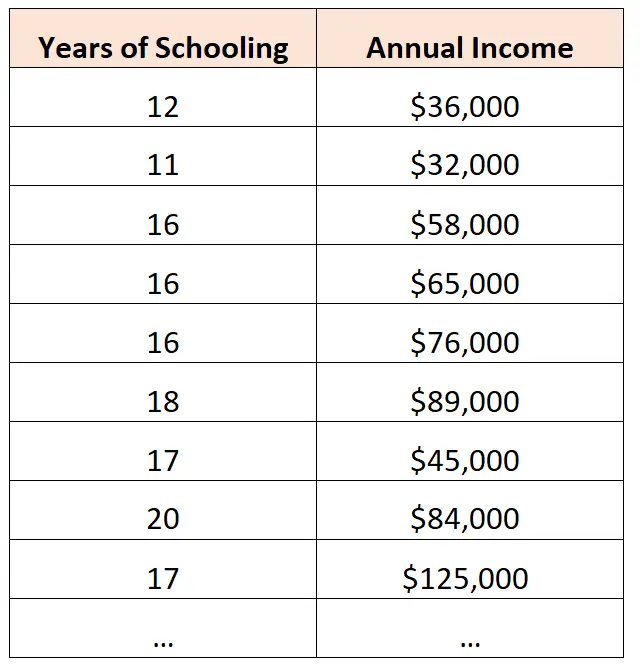
Anschließend kann er entscheiden, das folgende einfache lineare Regressionsmodell anzupassen:

Jahreseinkommen = -45.353 + 7.120*(Schuljahre)

Dem Ökonomen zufolge steigt das Jahreseinkommen mit jedem weiteren Schuljahr um durchschnittlich 7.120 US-Dollar.

Beispiel 5: Biologie

Biologen sammeln häufig bivariate Daten, um zu verstehen, wie zwei Variablen zwischen Pflanzen oder Tieren zusammenhängen.

Ein Biologe könnte beispielsweise Daten zum Gesamtniederschlag und zur Gesamtzahl der Pflanzen in verschiedenen Regionen sammeln:

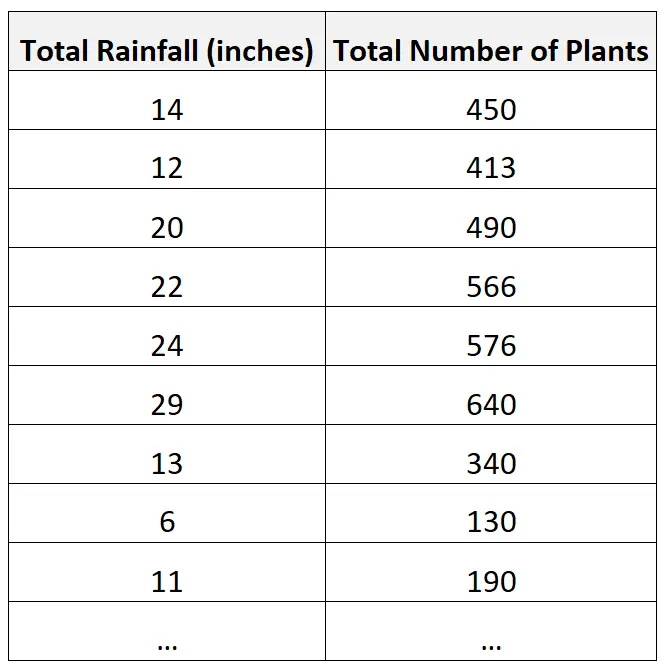
Der Biologe kann dann entscheiden, die Korrelation zwischen den beiden Variablen zu berechnen und einen Wert von 0,926 zu ermitteln.

Dies deutet darauf hin, dass zwischen den beiden Variablen eine starke positive Korrelation besteht.

Das heißt, höhere Niederschläge sind eng mit einer erhöhten Pflanzenzahl in einer Region verbunden.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zu bivariaten Daten und deren Analyse.

Einführung in die bivariate Analyse
Einführung in die univariate Analyse
Einführung in den Pearson-Korrelationskoeffizienten
Einführung in die einfache lineare Regression