So simulieren und zeichnen sie eine bivariate normalverteilung in r

In der Statistik folgen zwei Variablen einer bivariaten Normalverteilung , wenn sie addiert eine Normalverteilung aufweisen.

In diesem Tutorial wird erläutert, wie Sie die folgenden Aufgaben in R ausführen:

• Simulieren Sie eine bivariate Normalverteilung
• Zeichnen Sie eine bivariate Normalverteilung mithilfe eines Konturdiagramms (2D-Diagramm)
• Zeichnen Sie eine bivariate Normalverteilung mithilfe eines Oberflächendiagramms (3D-Diagramm)

Lass uns gehen!

Beispiel 1: Simulieren Sie eine bivariate Normalverteilung in R

Der einfachste Weg, eine bivariate Normalverteilung in R zu simulieren, ist die Verwendung der Funktion mvrnorm() aus dem MASS- Paket.

Der folgende Code zeigt, wie diese Funktion zur Simulation einer bivariaten Normalverteilung in der Praxis verwendet wird:

 library (MASS)

#make this example reproducible
set. seed ( 0 )

#simulate bivariate normal distribution
bivariate_data <- as. data . frame (mvrnorm(n= 100 ,
                                        mu=c(0, 0),
                                        Sigma=matrix(c(5, 3, 4, 4), ncol= 2 )))

#view first six rows of bivariate dataset
head(bivariate_data)

           V1 V2
1 -2.03600343 -2.9623059
2 0.07719131 1.2948982
3 -3.26729701 -1.7928069
4 -2.62985132 -2.3015471
5 -1.75126215 0.3056698
6 3.67698436 2.2020238

Hier ist, was jedes Argument der mvrnorm()- Funktion bewirkt:

• n : Definiert die Stichprobengröße
• mu : Definiert den Durchschnitt jeder Variablen
• Sigma : Definiert die Kovarianzmatrix der beiden Variablen

Das Endergebnis ist ein Datenrahmen mit zwei Variablen, die bei Addition einer Normalverteilung folgen.

Beispiel 2: Zeichnen einer bivariaten Normalverteilung

Der einfachste Weg, eine bivariate Normalverteilung in R darzustellen, ist die Verwendung der Funktionen im mnormt() -Paket.

Beispielsweise können wir die Funktion context() dieses Pakets verwenden, um ein Konturdiagramm zu erstellen, das eine 2D-Visualisierung der bivariaten Normalverteilung bereitstellt:

 library (mnormt)

#make this example reproducible
set. seed ( 0 )

#create bivariate normal distribution
x <- seq(-3, 3, 0.1) 
y <- seq(-3, 3, 0.1)
mu <- c(0, 0)
sigma <- matrix(c(2, -1, -1, 2), nrow= 2 )
f <- function(x, y) dmnorm(cbind(x, y), mu, sigma)
z <- outer(x, y, f)

#create contour plot
contour(x, y, z)

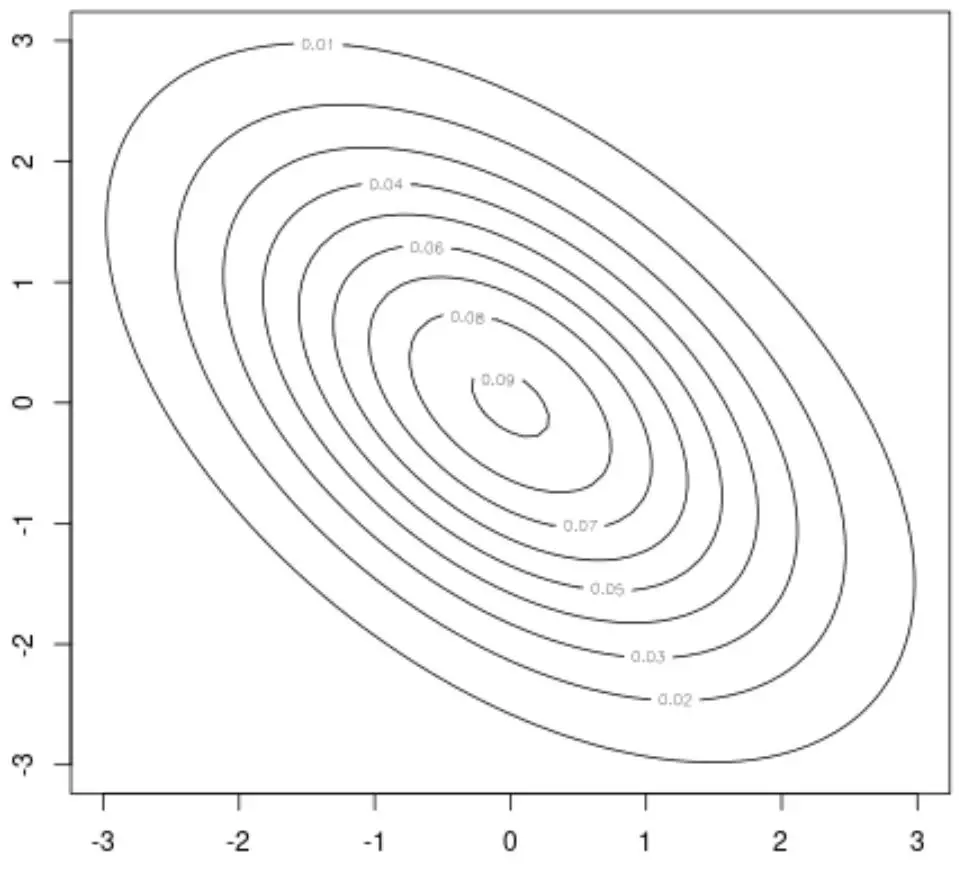
Wir können auch die Funktion persp() verwenden, um ein Oberflächendiagramm zu erstellen, das eine 3D-Visualisierung der bivariaten Normalverteilung bietet:

 library (mnormt)

#make this example reproducible
set. seed ( 0 )

#create bivariate normal distribution
x <- seq(-3, 3, 0.1) 
y <- seq(-3, 3, 0.1)
mu <- c(0, 0)
sigma <- matrix(c(2, -1, -1, 2), nrow= 2 )
f <- function(x, y) dmnorm(cbind(x, y), mu, sigma)
z <- outer(x, y, f)

#create surface plot
persp(x, y, z, theta= -30 , phi= 25 , expand= 0.6 , ticktype=' detailed ')

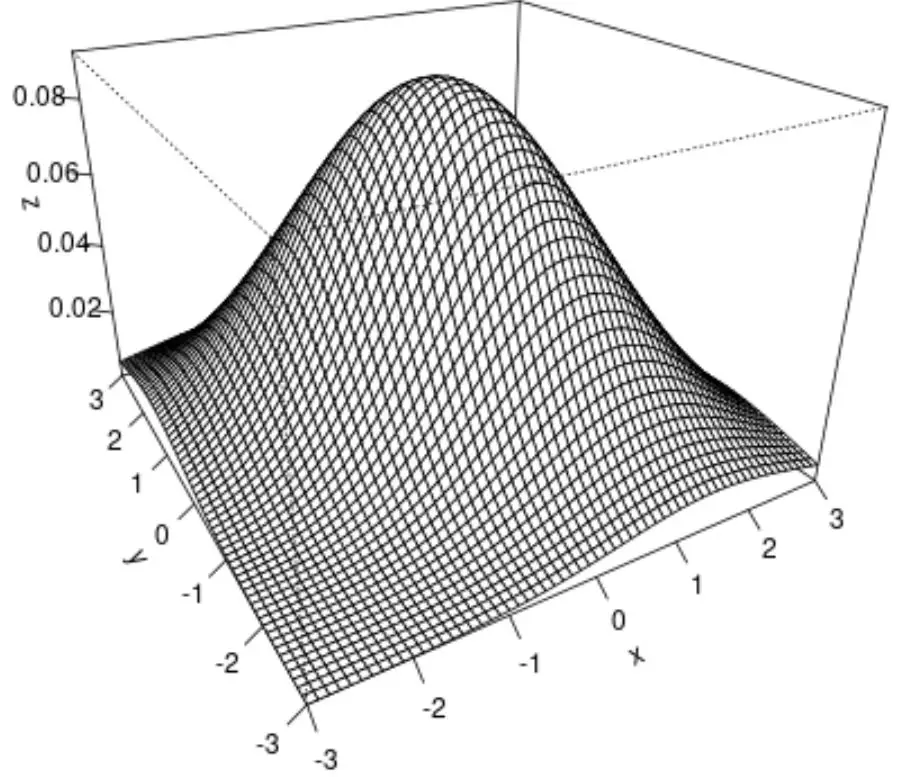
Hier ist, was jedes Argument der persp() -Funktion bewirkt:

• Theta, Phi : Legt die Blickrichtungswinkel fest.
• expand : Steuert die Größe der Z-Achse.
• ticktype : Steuert das Erscheinungsbild von Häkchen auf den Achsen.

Das Endergebnis ist ein 3D-Oberflächendiagramm der bivariaten Normalverteilung.

Zusätzliche Ressourcen

Die folgenden Tutorials erklären, wie man andere Wahrscheinlichkeitsverteilungen in R verwendet:

So verwenden Sie die Normalverteilung in R
Wie man die Binomialverteilung in R verwendet
So verwenden Sie die Poisson-Verteilung in R
Wie man die Multinomialverteilung in R verwendet