So führen sie den white-test in sas durch

Der White-Test wird verwendet, um festzustellen, ob in einem Regressionsmodell Heteroskedastizität vorliegt.

Unter Heteroskedastizität versteht man die ungleichmäßige Streuung der Residuen auf verschiedenen Ebenen einer Antwortvariablen in einem Regressionsmodell, was gegen eine der Schlüsselannahmen der linearen Regression verstößt, dass Residuen auf jeder Ebene der Antwortvariablen gleichmäßig verteilt sind.

In diesem Tutorial wird erläutert, wie Sie den White-Test in SAS durchführen, um festzustellen, ob Heteroskedastizität in einem bestimmten Regressionsmodell ein Problem darstellt.

Beispiel: Weißtest in SAS

Angenommen, wir möchten ein multiples lineares Regressionsmodell anpassen, das die Anzahl der Lernstunden und die Anzahl der abgelegten Übungsprüfungen verwendet, um die Abschlussnote der Schüler vorherzusagen:

Prüfungsergebnis = β ₀ + β ₁ (Stunden) + β ₂ (Vorprüfungen)

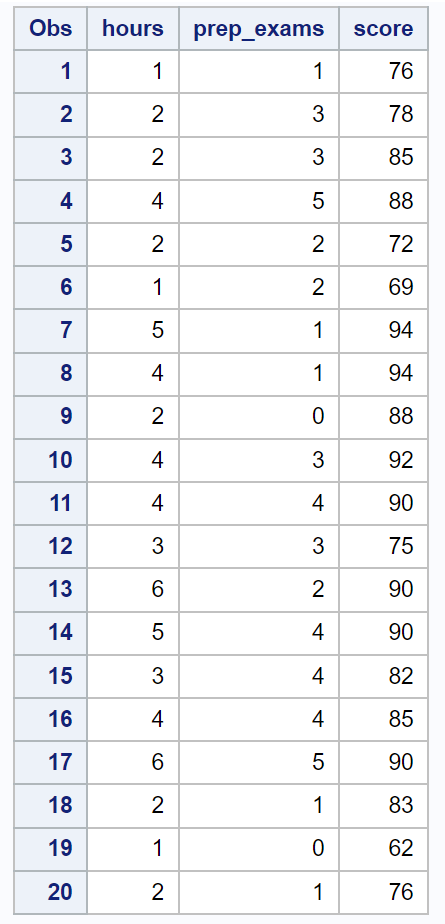
Zuerst verwenden wir den folgenden Code, um einen Datensatz mit diesen Informationen für 20 Schüler zu erstellen:

 /*create dataset*/
data exam_data;
    input hours prep_exams score;
    datalines ;
1 1 76
2 3 78
2 3 85
4 5 88
2 2 72
1 2 69
5 1 94
4 1 94
2 0 88
4 3 92
4 4 90
3 3 75
6 2 90
5 4 90
3 4 82
4 4 85
6 5 90
2 1 83
1 0 62
2 1 76
;
run ;

/*view dataset*/
proc print data =exam_data; 

Als nächstes verwenden wir proc reg, um dieses multiple lineare Regressionsmodell anzupassen, sowie die spec- Option, um den White-Test auf Heteroskedastizität durchzuführen:

 /*fit regression model and perform White's test*/
proc reg data =exam_data;
    model score = hours prep_exams / spec ;
run ;
quit ; 

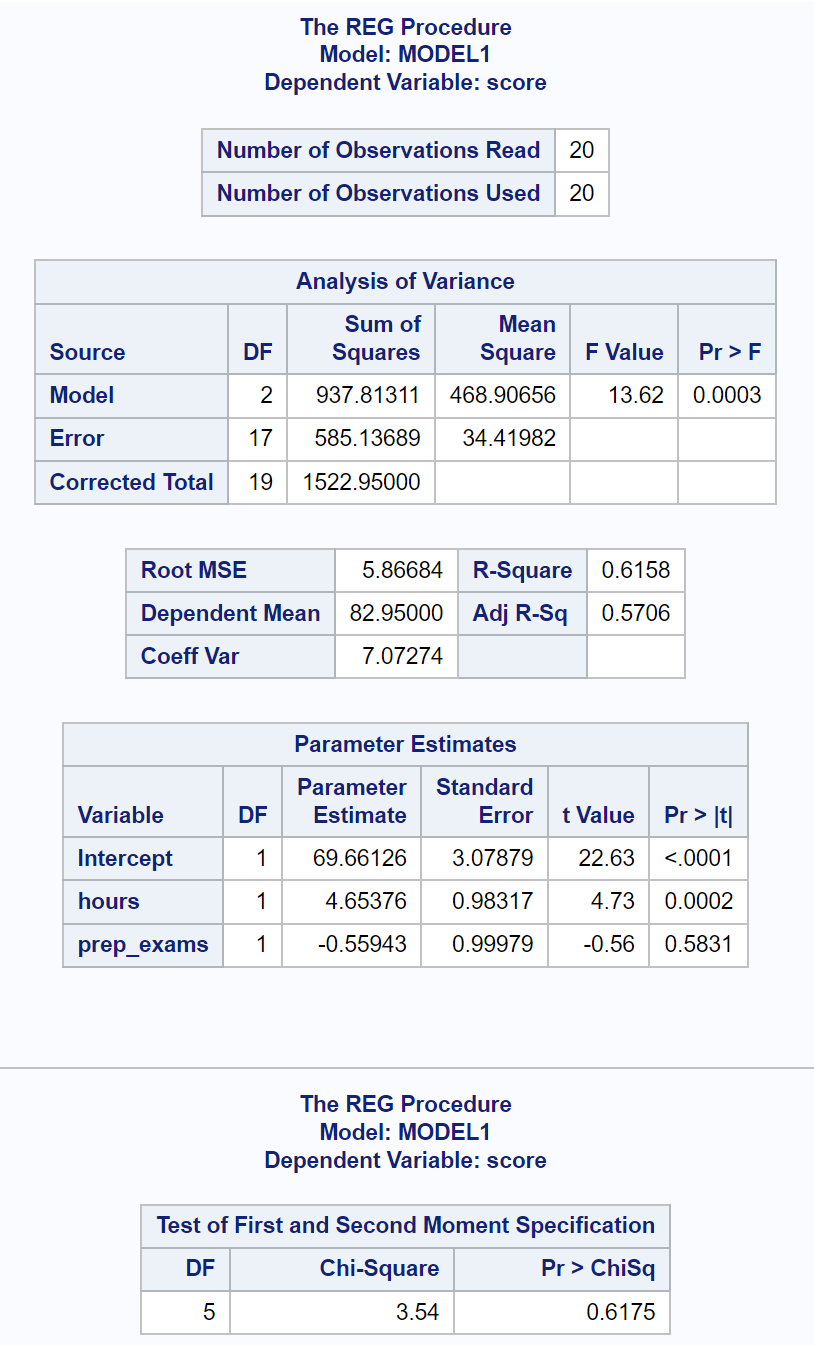
Die letzte Ergebnistabelle zeigt die Ergebnisse des weißen Tests.

Aus dieser Tabelle können wir ersehen, dass die Chi-Quadrat-Teststatistik 3,54 und der entsprechende p-Wert 0,6175 beträgt.

Der White-Test verwendet die folgenden Null- und Alternativhypothesen:

• Null (H ₀ ) : Heteroskedastizität ist nicht vorhanden.
• Alternative ( _HA ): Heteroskedastizität liegt vor.

Da der p-Wert nicht kleiner als 0,05 ist, können wir die Nullhypothese nicht ablehnen.

Dies bedeutet, dass wir nicht über ausreichende Beweise verfügen, um zu behaupten, dass Heteroskedastizität im Regressionsmodell vorhanden ist.

Daher ist es möglich, die Standardfehler der Koeffizientenschätzungen in der Regressionsübersichtstabelle sicher zu interpretieren.

Was macht man als nächstes

Wenn Sie die Nullhypothese des White-Tests nicht ablehnen, liegt keine Heteroskedastizität vor und Sie können mit der Interpretation des Ergebnisses der ursprünglichen Regression fortfahren.

Wenn Sie jedoch die Nullhypothese ablehnen, bedeutet dies, dass in den Daten Heteroskedastizität vorliegt. In diesem Fall sind die in der Regressionsausgabetabelle angezeigten Standardfehler möglicherweise unzuverlässig.

Es gibt mehrere gängige Möglichkeiten, dieses Problem zu lösen, darunter:

1. Transformieren Sie die Antwortvariable. Sie können versuchen, eine Transformation für die Antwortvariable durchzuführen.

Sie können beispielsweise die Protokollantwortvariable anstelle der ursprünglichen Antwortvariablen verwenden.

Im Allgemeinen ist die Protokollierung der Antwortvariablen eine wirksame Methode, um die Heteroskedastizität zu beseitigen.

Eine weitere übliche Transformation besteht darin, die Quadratwurzel der Antwortvariablen zu verwenden.

2. Verwenden Sie eine gewichtete Regression. Diese Art der Regression weist jedem Datenpunkt basierend auf der Varianz seines angepassten Werts eine Gewichtung zu.

Dadurch erhalten Datenpunkte mit höheren Varianzen kleine Gewichtungen, wodurch ihre Restquadrate reduziert werden.

Durch die Verwendung geeigneter Gewichte kann das Problem der Heteroskedastizität beseitigt werden.