Blockierung in statistiken: definition und beispiel

In Experimenten möchten Forscher häufig die Beziehung zwischen einer erklärenden Variablen und einer Antwortvariablen verstehen.

Leider treten in experimentellen Studien häufig störende Variablen auf, bei denen es sich um Variablen handelt, die die Beziehung zwischen der erklärenden Variablen und der Antwortvariablen beeinflussen, für Forscher jedoch nicht von Interesse sind.

Angenommen, Forscher möchten die Wirkung einer neuen Diät auf die Gewichtsabnahme verstehen. Die erklärende Variable ist die neue Ernährung und die Antwortvariable ist der Grad des Gewichtsverlusts.

Eine Störungsvariable, die zu Abweichungen führen kann, ist jedoch das Geschlecht . Es ist wahrscheinlich, dass das Geschlecht einer Person Einfluss darauf hat, wie viel Gewicht sie verliert, unabhängig davon, ob die neue Diät funktioniert oder nicht.

Blockierungsübersicht

Eine gängige Methode zur Kontrolle der Wirkung von Störvariablen ist die Blockierung , bei der Personen in einem Experiment auf der Grundlage des Werts einer Störvariablen aufgeteilt werden.

In unserem vorherigen Beispiel würden wir Personen in einen der folgenden zwei Blöcke einordnen:

• Männlich
• Weiblich

Dann würden wir innerhalb jedes Blocks Einzelpersonen nach dem Zufallsprinzip einer von zwei Behandlungen zuordnen:

• Eine neue Diät
• Eine Standarddiät

Auf diese Weise wäre die Variation innerhalb jedes Blocks viel geringer als die Variation zwischen allen Individuen und wir könnten besser verstehen, wie sich die neue Diät auf die Gewichtsabnahme auswirkt und gleichzeitig das Geschlecht kontrolliert.

Um dies zu veranschaulichen, betrachten Sie die folgende Tabelle, die den Gesamtgewichtsverlust von 16 an der Studie teilnehmenden Personen zeigt:

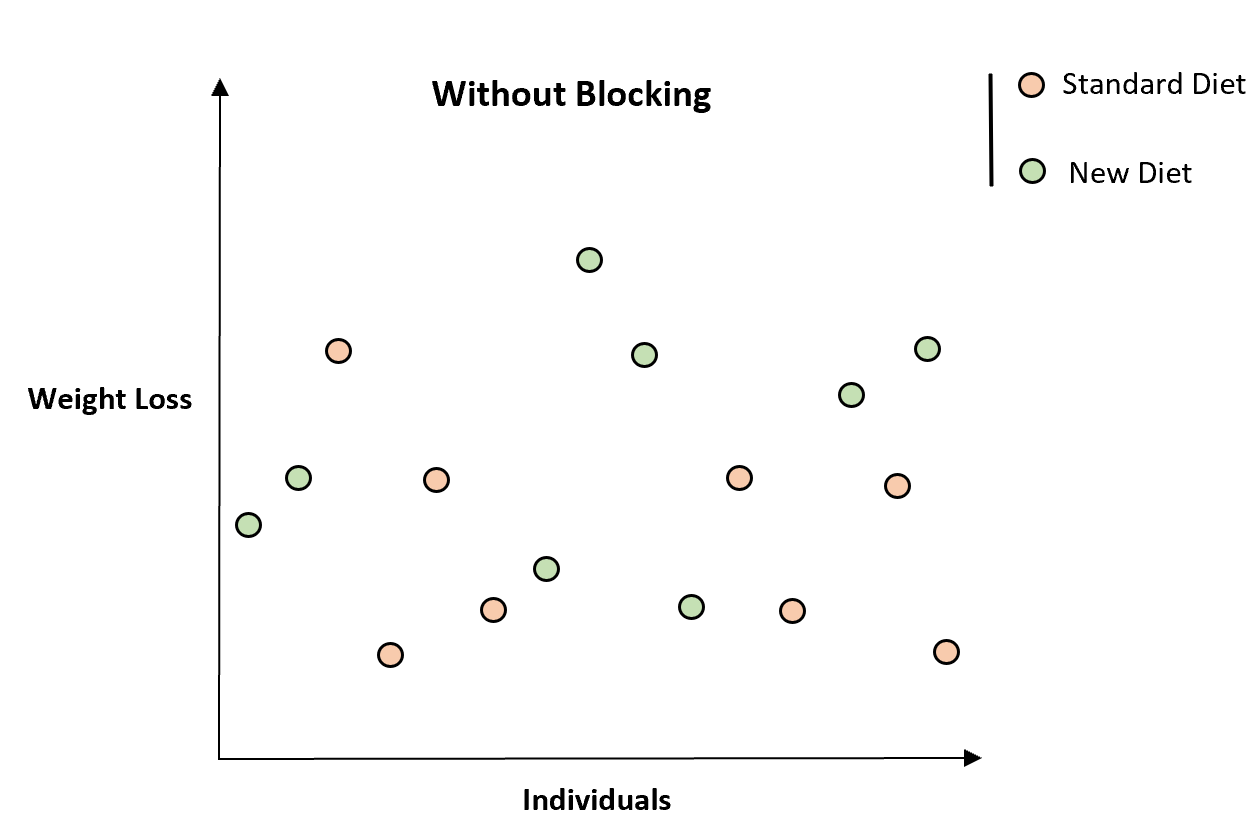
Auf den ersten Blick sieht es nicht so aus, als ob die neue Diät mit einer erhöhten Gewichtsabnahme einhergeht.

Wenn wir die Personen jedoch nach Geschlecht in zwei Blöcke einteilen, wird deutlich, dass die neue Ernährung offenbar mit einem erhöhten Gewichtsverlust verbunden ist:

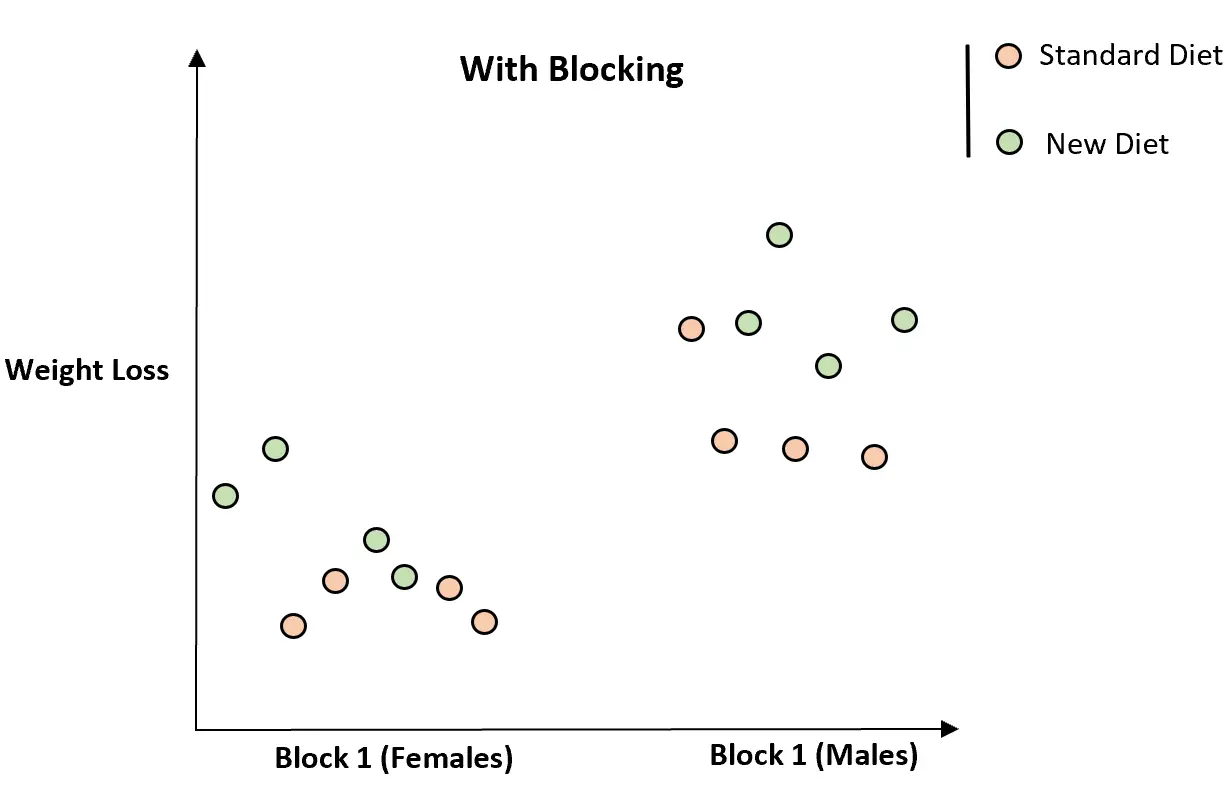
Durch die Einteilung einzelner Personen in Blöcke wurde der Zusammenhang zwischen der neuen Ernährung und dem Gewichtsverlust klarer, da wir die störende Variable des Geschlechts kontrollieren konnten.

Weitere Blockierungsbeispiele

Das Geschlecht ist eine häufige Störvariable, die in Experimenten als Blockierungsfaktor verwendet wird, da Männer und Frauen tendenziell unterschiedlich auf eine Vielzahl von Behandlungen reagieren.

Zu den weiteren häufigen Störgrößen, die als Blockierungsfaktoren verwendet werden können, gehören jedoch:

• Altersspanne
• Einkommensgruppe
• Bildungsgrad
• Umfang der Bewegung
• Region

Abhängig von der Art des Experiments ist es auch möglich, mehrere Blockierungsfaktoren gleichzeitig zu verwenden. In der Praxis werden jedoch meist nur ein oder zwei verwendet, da mehr Blockierungsfaktoren größere Stichprobengrößen erfordern, um aussagekräftige Ergebnisse zu erhalten.

Schädliche Variablen und versteckte Variablen

Im vorherigen Beispiel war das Geschlecht eine bekannte Störungsvariable, von der Forscher annahmen, dass sie den Gewichtsverlust beeinflusste. Allerdings gibt es in Experimenten häufig auchversteckte Variablen , also Variablen, die ebenfalls die Beziehung zwischen einer erklärenden Variablen und einer Antwortvariablen beeinflussen, die aber entweder unbekannt sind oder einfach nicht in die Studie einbezogen werden, weil es schwierig ist, Daten über sie zu sammeln.

Nehmen wir zum Beispiel an, dass jeder Mensch über eine gewisse angeborene Disziplin verfügt, auf die er sich verlassen kann, um mehr Gewicht zu verlieren. Da Disziplin schwer zu messen ist, wird sie nicht als blockierender Faktor in die Studie einbezogen, aber eine Möglichkeit, sie zu kontrollieren, ist die Verwendung von Randomisierung .

Durch die zufällige Zuweisung von Personen zur neuen Diät oder zur Standarddiät können Forscher die Chance maximieren, dass das Gesamtniveau der Disziplin der Personen in den beiden Gruppen ungefähr gleich ist.

Daher ist es in jedem Blockierungsexperiment auch wichtig, Einzelpersonen nach dem Zufallsprinzip Behandlungen zuzuordnen, um die Auswirkungen potenzieller versteckter Variablen zu kontrollieren.

Zusätzliche Ressourcen

Erklärende Variablen und Antwortvariablen
Versteckte Variablen
Passendes Paar-Design
Gestaltung geteilter Grundstücke