So führen sie eine bonferroni-korrektur in excel durch

Eine Bonferroni-Korrektur bezieht sich auf den Prozess der Anpassung des Alpha-Werts (α) für eine Familie statistischer Tests, um die Wahrscheinlichkeit eines Typ-I-Fehlers zu kontrollieren.

Die Formel für eine Bonferroni-Korrektur lautet wie folgt:

α _neu = α _original / n

Gold:

• _{ursprüngliches} α: Das ursprüngliche α-Niveau
• n: Die Gesamtzahl der durchgeführten Vergleiche oder Tests

Wenn wir beispielsweise drei statistische Tests gleichzeitig ausführen und für jeden Test α = 0,05 verwenden möchten, sagt uns die Bonferroni-Korrektur, dass wir α _new = 0,01667 verwenden sollten.

_neues α = _{ursprüngliches} α / n = 0,05 / 3 = 0,01667

Daher sollten wir die Nullhypothese jedes einzelnen Tests nur dann ablehnen, wenn der p-Wert des Tests kleiner als 0,01667 ist.

Diese Art der Korrektur wird häufig in Post-hoc-Tests im Anschluss an eine ANOVA durchgeführt, wenn wir mehrere Gruppenmittelwerte gleichzeitig vergleichen möchten.

Das folgende Schritt-für-Schritt-Beispiel zeigt, wie Sie eine Bonferroni-Korrektur nach einer einfaktoriellen ANOVA in Excel durchführen.

Schritt 1: Erstellen Sie die Daten

Erstellen wir zunächst einen gefälschten Datensatz, der die Ergebnisse von Studenten zeigt, die eine von drei verschiedenen Lerntechniken zur Vorbereitung auf die Prüfung verwendet haben:

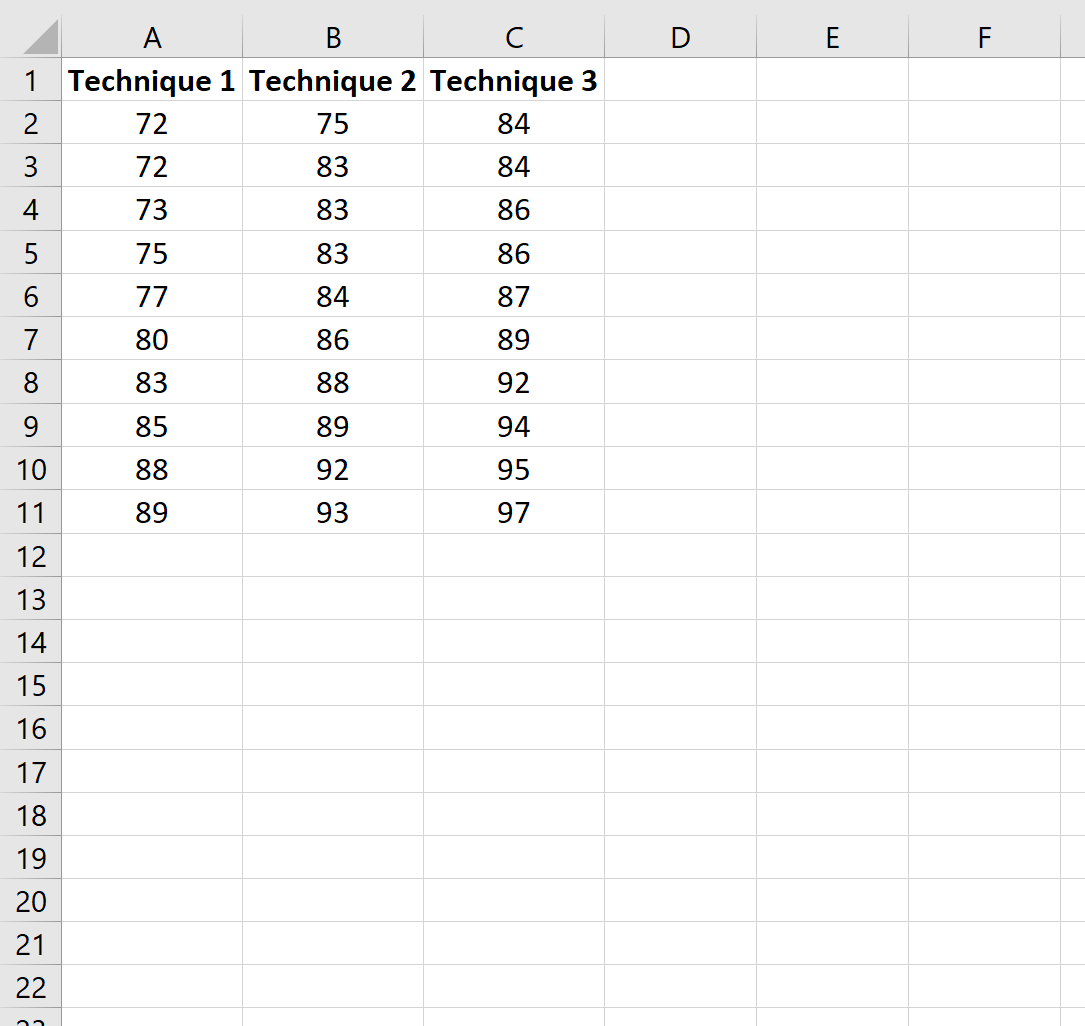
Schritt 2: Führen Sie eine einfaktorielle ANOVA durch

Als Nächstes führen wir eine einfache ANOVA durch, um festzustellen, ob die durchschnittlichen Prüfungsergebnisse in den drei Gruppen gleich sind.

Markieren Sie zunächst alle Daten, einschließlich der Spaltenüberschriften:

Klicken Sie anschließend im oberen Menüband auf die Registerkarte „Daten“ und dann auf „Datenanalyse“ :

Wenn diese Option nicht verfügbar ist, müssen Sie zuerst Analysis ToolPak laden .

Klicken Sie im angezeigten Fenster auf Anova: Single Factor und dann auf OK .

Vervollständigen Sie die folgenden Informationen und klicken Sie dann auf OK :

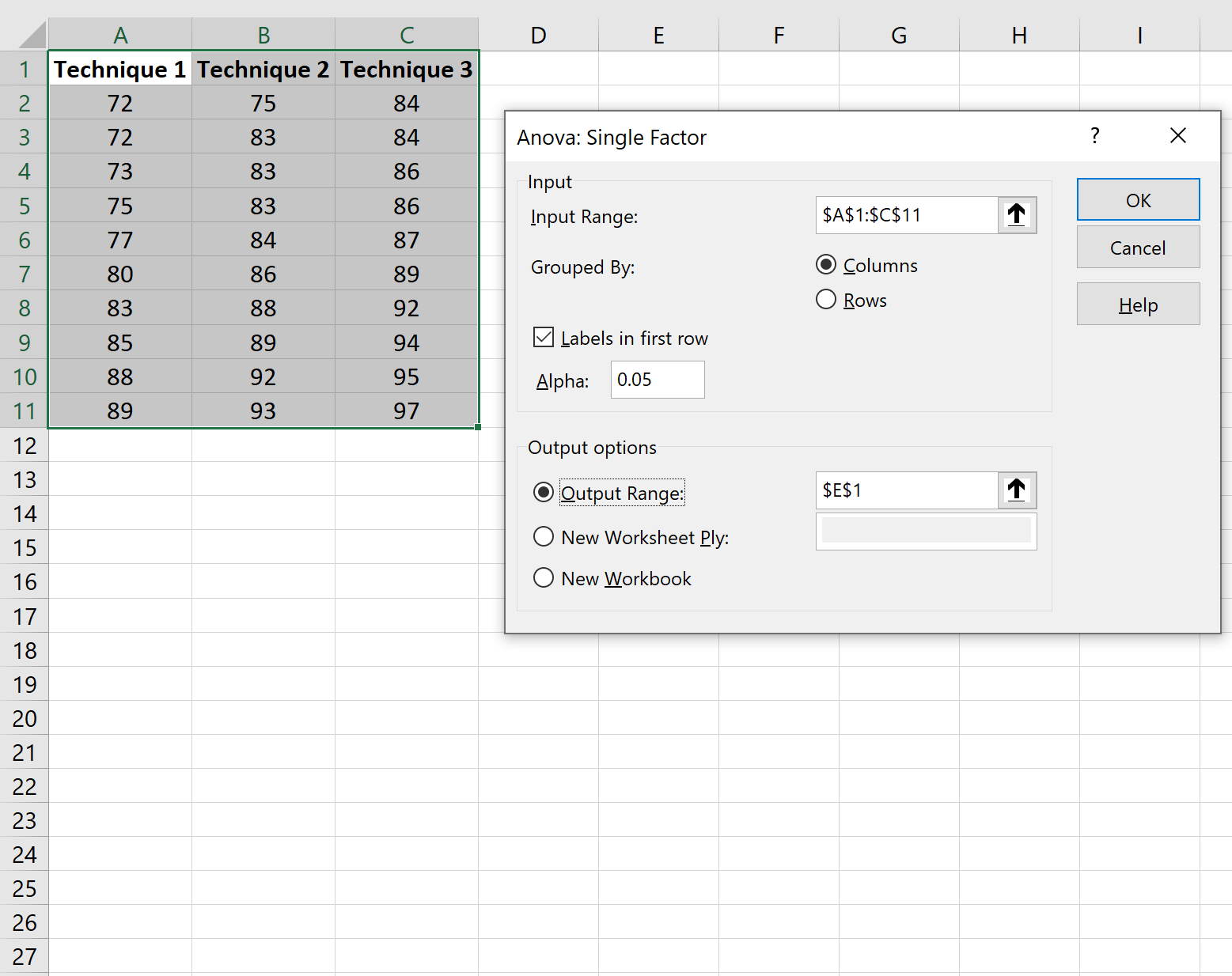
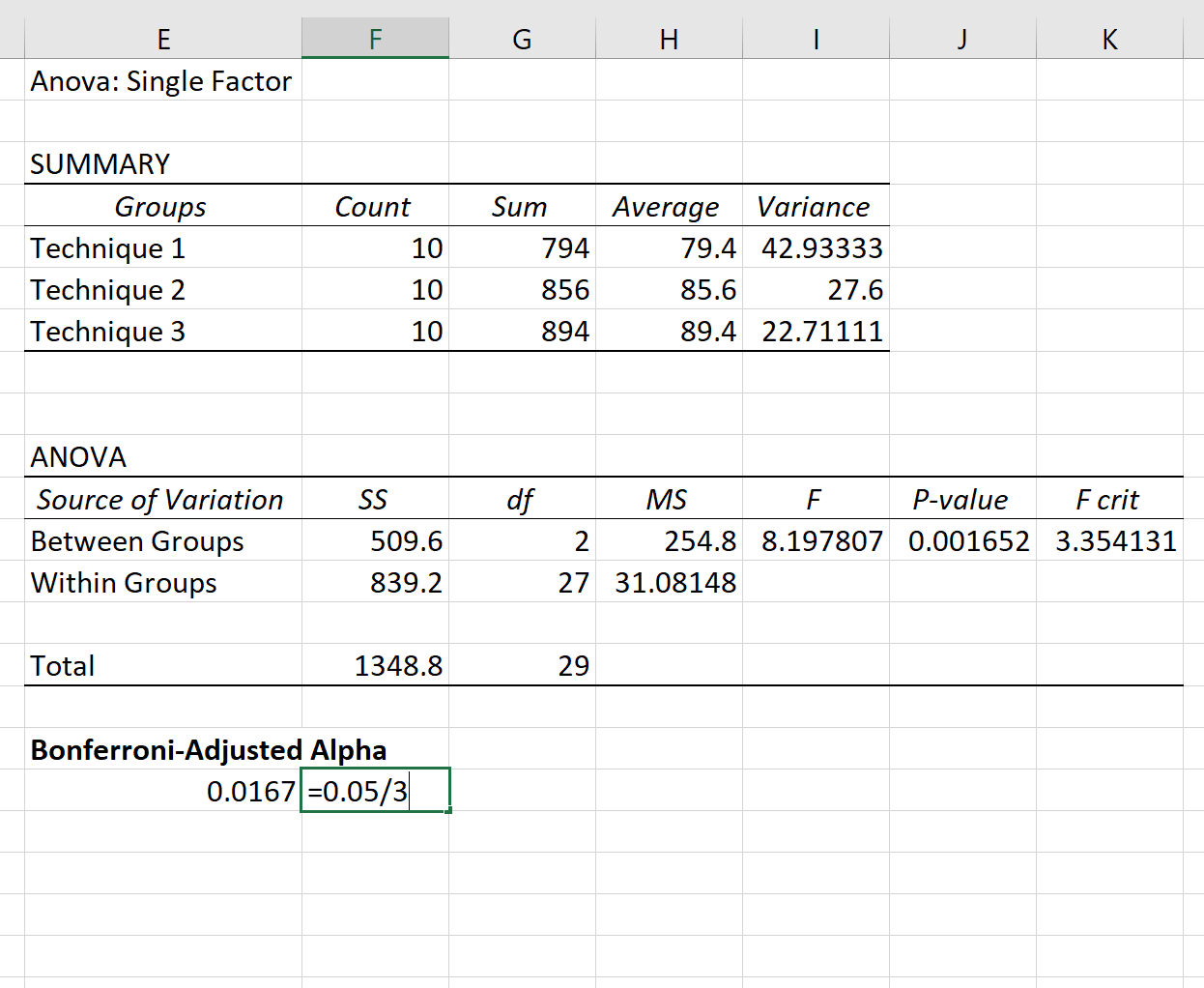
Die Ergebnisse der einfaktoriellen ANOVA werden automatisch angezeigt:

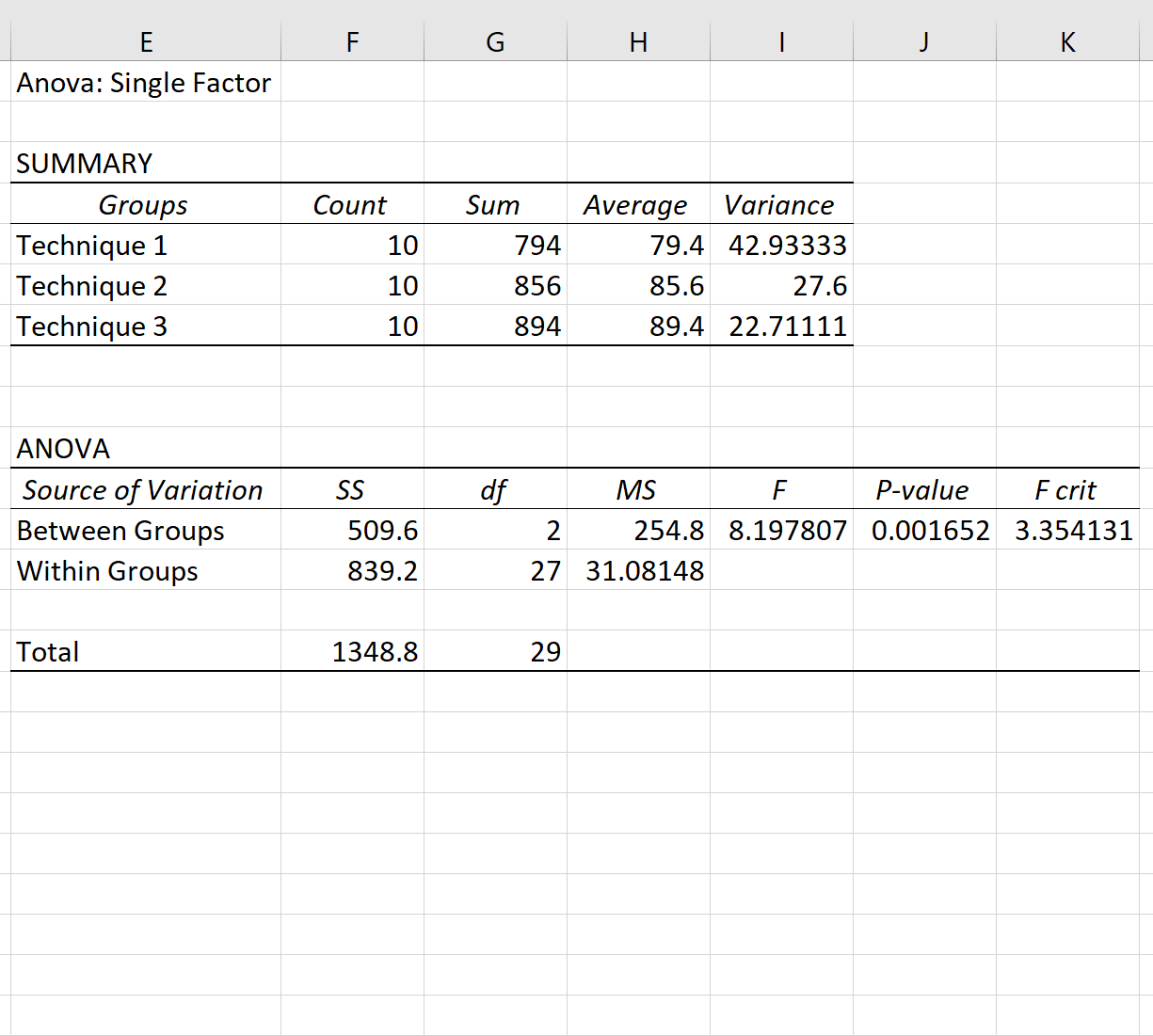
Denken Sie daran, dass eine einfaktorielle ANOVA die folgenden Null- und Alternativhypothesen hat:

• H ₀ (Nullhypothese): Alle Gruppenmittelwerte sind gleich.
• H _A (Alternativhypothese): Mindestens ein Gruppenmittelwert ist unterschiedlich   ausruhen.

Da der p-Wert in der ANOVA-Tabelle (0,001652) kleiner als 0,05 ist, haben wir genügend Beweise, um die Nullhypothese abzulehnen. Mit anderen Worten: Die durchschnittlichen Prüfungsergebnisse der drei Gruppen sind nicht gleich.

Dann können wir mithilfe einer Bonferroni-Korrektur mehrere Vergleiche zwischen den drei Gruppen anstellen, um genau zu sehen, welche Gruppenmittelwerte unterschiedlich sind.

Schritt 3: Führen Sie mehrere Vergleiche mithilfe einer Bonferroni-Korrektur durch

Mithilfe einer Bonferroni-Korrektur können wir den angepassten Alpha-Wert wie folgt berechnen:

α _neu = α _original / n

In unserem Beispiel führen wir die folgenden drei Vergleiche durch:

• Technik 1 versus Technik 2
• Technik 1 versus Technik 3
• Technik 2 versus Technik 3

Da wir für jeden Test α = .05 verwenden möchten, sagt uns die Bonferroni-Korrektur, dass wir α _new = .0167 verwenden sollten.

Als nächstes verwenden wir einen T-Test, um die Mittelwerte zwischen den einzelnen Gruppen zu vergleichen. In Excel können Sie die folgende Syntax verwenden:

=TTEST(Tabelle1, Tabelle2, Warteschlangen=2, Typ=2)

Gold:

• Array1: das erste Datenarray
• Array2: das zweite Datenarray
• tails: Die Anzahl der Tails im Test. Wir verwenden „2“, um einen zweiseitigen Test anzuzeigen.
• Typ: Der Typ des durchzuführenden T-Tests. Wir verwenden „2“, um einen T-Test mit gleichen Varianzen anzuzeigen.

Der folgende Screenshot zeigt, wie die einzelnen T-Tests durchgeführt werden:

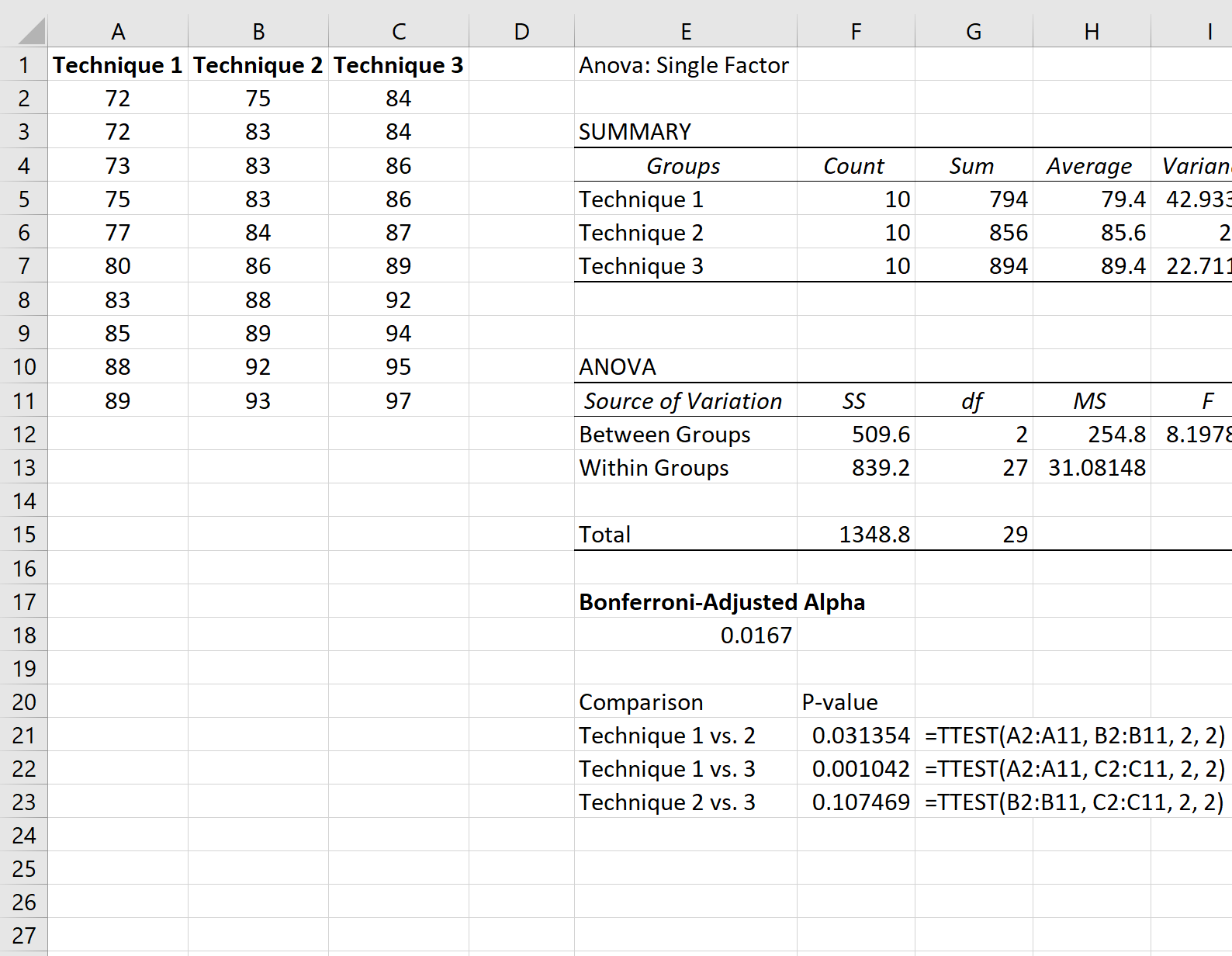
Der einzige p-Wert unterhalb des Bonferroni-bereinigten Alpha-Werts stammt aus dem Vergleich zwischen Technik 1 und Technik 2, der einen p-Wert von 0,001042 hatte.

Daraus würden wir schließen, dass nur der statistisch signifikante Unterschied in den durchschnittlichen Prüfungsergebnissen zwischen Technik 1 und Technik 2 bestand.

Zusätzliche Ressourcen

Wie hoch ist die Fehlerquote pro Familie?
Die Bonferroni-Korrektur: Definition und Beispiel
Bonferroni-Korrekturrechner