So führen sie eine bonferroni-korrektur in r durch

Eine einfaktorielle ANOVA wird verwendet, um zu bestimmen, ob ein statistisch signifikanter Unterschied zwischen den Mittelwerten von drei oder mehr unabhängigen Gruppen besteht.

Wenn der Gesamt -p-Wert der ANOVA-Tabelle unter einem bestimmten Signifikanzniveau liegt, verfügen wir über ausreichende Beweise dafür, dass sich mindestens einer der Gruppenmittelwerte von den anderen unterscheidet.

Dies sagt uns jedoch nicht, welche Gruppen sich voneinander unterscheiden. Dies zeigt uns einfach, dass nicht alle Gruppendurchschnitte gleich sind.

Um genau zu wissen, welche Gruppen sich voneinander unterscheiden, müssen wir paarweise t-Tests zwischen jeder Gruppe durchführen und dabei die Familienfehlerrate kontrollieren.

Eine der gebräuchlichsten Methoden, dies zu erreichen, ist die Verwendung der Bonferroni-Korrektur bei der Berechnung der p-Werte für jeden der paarweisen t-Tests.

In diesem Tutorial wird erklärt, wie die Bonferroni-Korrektur in R durchgeführt wird.

Beispiel: Bonferroni-Korrektur in R

Angenommen, ein Lehrer möchte wissen, ob drei verschiedene Lerntechniken zu unterschiedlichen Testergebnissen bei den Schülern führen.

Um dies zu testen, weist sie nach dem Zufallsprinzip 10 Studenten zu, jede Lerntechnik anzuwenden. Nachdem jeder Schüler eine Woche lang die ihm zugewiesene Lerntechnik angewendet hat, legt er die gleiche Prüfung ab.

Wir können die folgenden Schritte in R verwenden, um eine einfaktorielle ANOVA anzupassen und die Bonferroni-Korrektur verwenden, um die paarweisen Unterschiede zwischen den Prüfungsergebnissen jeder Gruppe zu berechnen.

Schritt 1: Erstellen Sie den Datensatz.

Der folgende Code zeigt, wie man einen Datensatz erstellt, der die Prüfungsergebnisse aller 30 Studenten enthält:

 #create data frame
data <- data.frame(technique = rep (c("tech1", "tech2", "tech3"), each = 10 ),
                   score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89,
                             81, 82, 83, 83, 83, 84, 87, 90, 92, 93,
                             77, 78, 79, 88, 89, 90, 91, 95, 95, 98))

#view first six rows of data frame
head(data)

  technical score
1 tech1 76
2 tech1 77
3 tech1 77
4 tech1 81
5 tech1 82
6 tech1 82

Schritt 2: Prüfungsergebnisse für jede Gruppe anzeigen.

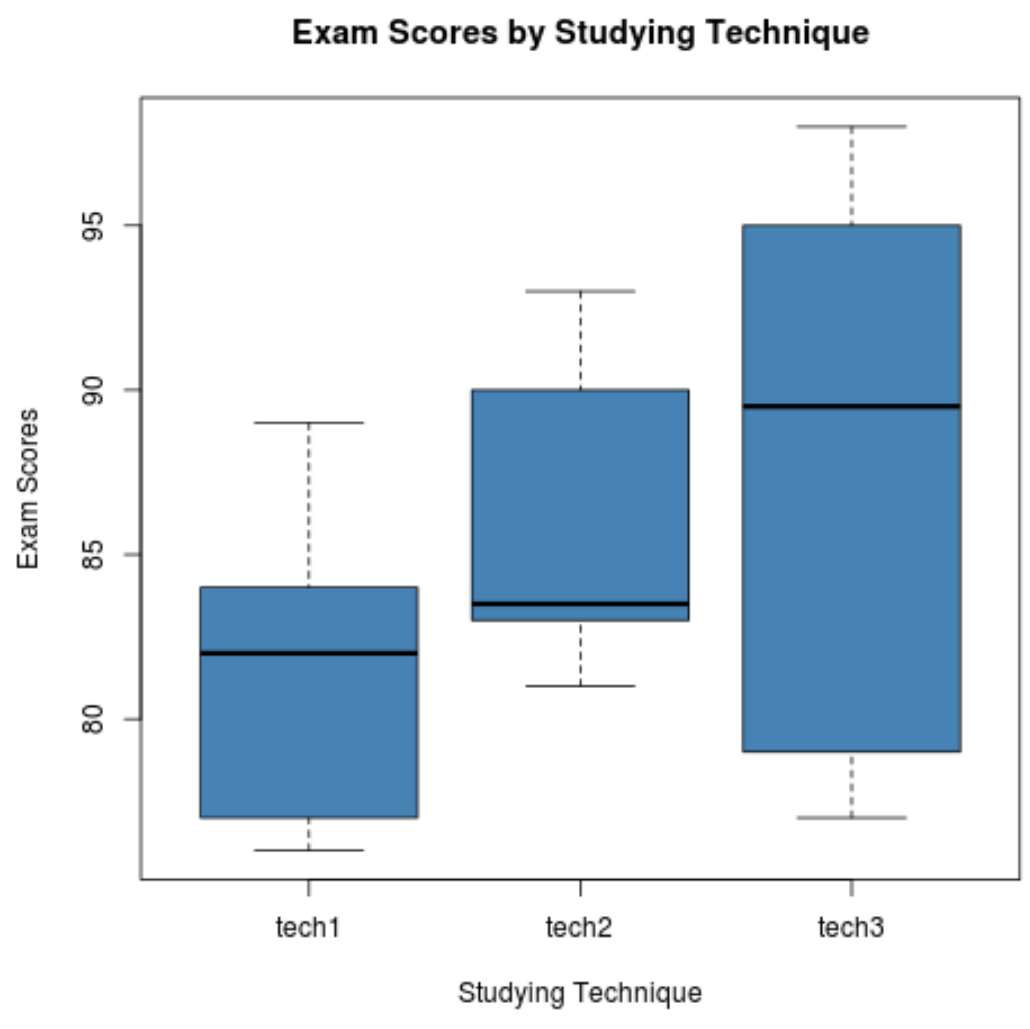
Der folgende Code zeigt, wie Boxplots erstellt werden, um die Verteilung der Prüfungsergebnisse für jede Gruppe zu visualisieren:

 boxplot(score ~ technique,
        data = data,
        main = "Exam Scores by Studying Technique",
        xlab = "Studying Technique",
        ylab = "Exam Scores",
        col = "steelblue",
        border = "black")

Schritt 3: Führen Sie eine einfaktorielle ANOVA durch.

Der folgende Code zeigt, wie eine einfaktorielle ANOVA durchgeführt wird, um Unterschiede zwischen den durchschnittlichen Prüfungsergebnissen in jeder Gruppe zu testen:

 #fit the one-way ANOVA model
model <- aov(score ~ technique, data = data)

#view model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)  
technical 2 211.5 105.73 3.415 0.0476 *
Residuals 27 836.0 30.96                 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Da der Gesamt-p-Wert ( 0,0476 ) kleiner als 0,05 ist, weist dies darauf hin, dass nicht jede Gruppe die gleiche durchschnittliche Prüfungspunktzahl aufweist.

Als nächstes führen wir paarweise T-Tests mit der Bonferroni-Korrektur für p-Werte durch, um paarweise Unterschiede zwischen den Prüfungsergebnissen jeder Gruppe zu berechnen.

Schritt 4: Führen Sie paarweise T-Tests durch.

Um paarweise t-Tests mit Bonferroni-Korrektur in R durchzuführen, können wir die Funktion pairwise.t.test() verwenden, die die folgende Syntax verwendet:

pairwise.t.test(x, g, p.adjust.method=“bonferroni“)

Gold:

• x: ein numerischer Vektor von Antwortwerten
• g: Ein Vektor, der die Namen von Gruppen angibt (z. B. Lerntechnik)

Der folgende Code zeigt, wie diese Funktion für unser Beispiel verwendet wird:

 #perform pairwise t-tests with Bonferroni's correction
pairwise.t.test(data$score, data$technique, p.adjust.method=" bonferroni ")

	Pairwise comparisons using t tests with pooled SD 

data: data$score and data$technique 

      tech1 tech2
tech2 0.309 -    
tech3 0.048 1.000

P value adjustment method: bonferroni

Das Ergebnis lässt sich wie folgt interpretieren:

• Der angepasste p-Wert für die mittlere Differenz der Prüfungsergebnisse zwischen Technik 1 und Technik 2 beträgt 0,309 .
• Der angepasste p-Wert für die mittlere Differenz der Prüfungsergebnisse zwischen Technik 1 und Technik 3 beträgt 0,048 .
• Der angepasste p-Wert für die mittlere Differenz der Prüfungsergebnisse zwischen Technik 2 und Technik 3 beträgt 1000 .

Anhand der Ergebnisse können wir erkennen, dass der einzige signifikante Unterschied zwischen Technik 1 und Technik 3 besteht.

Zusätzliche Ressourcen

Eine Einführung in die einfaktorielle ANOVA
So führen Sie eine einfaktorielle ANOVA in R durch
So führen Sie den Tukey-Test in R durch
So führen Sie den Dunnett-Test in R durch