Bootstrapping in r (mit beispielen)

Bootstrapping ist eine Methode, mit der der Standardfehler jeder Statistik geschätzt und einKonfidenzintervall für die Statistik erstellt werden kann.

Der grundlegende Prozess für das Bootstrapping ist wie folgt:

• Nehmen Sie k Replikatproben mit Ersetzung aus einem bestimmten Datensatz.
• Berechnen Sie für jede Stichprobe die interessierende Statistik.
• Dies ergibt k verschiedene Schätzungen für eine bestimmte Statistik, die Sie dann verwenden können, um den Standardfehler der Statistik zu berechnen und ein Konfidenzintervall für die Statistik zu erstellen.

Wir können in R mit den folgenden Funktionen aus der Bootstrap-Bibliothek booten:

1. Bootstrap-Beispiele generieren.

boot(Daten, Statistiken, R, …)

Gold:

• Daten: ein Vektor, eine Matrix oder ein Datenblock
• Statistik: eine Funktion, die die zu initiierende(n) Statistik(en) erstellt
• A: Anzahl der Bootstrap-Wiederholungen

2. Generieren Sie ein Bootstrap-Konfidenzintervall.

boot.ci(Boot-Objekt, Konfiguration, Typ)

Gold:

• Bootobject: Ein von der Funktion boot() zurückgegebenes Objekt
• conf: Das zu berechnende Konfidenzintervall. Der Standardwert ist 0,95
• Typ: Typ des zu berechnenden Konfidenzintervalls. Zu den Optionen gehören „Standard“, „Basic“, „Stud“, „Perc“, „Bca“ und „All“ – die Standardeinstellung ist „All“.

Die folgenden Beispiele zeigen, wie Sie diese Funktionen in der Praxis nutzen können.

Beispiel 1: Bootstrap einer einzelnen Statistik

Der folgende Code zeigt, wie der Standardfehler für dasR-Quadrat eines einfachen linearen Regressionsmodells berechnet wird:

 set.seed(0)
library (boot)

#define function to calculate R-squared
rsq_function <- function (formula, data, indices) {
  d <- data[indices,] #allows boot to select sample
  fit <- lm(formula, data=d) #fit regression model
  return (summary(fit)$r.square) #return R-squared of model
}
#perform bootstrapping with 2000 replications
reps <- boot(data=mtcars, statistic=rsq_function, R=2000, formula=mpg~disp)

#view results of boostrapping
reps

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = mtcars, statistic = rsq_function, R = 2000, formula = mpg ~ 
    available)


Bootstrap Statistics:
     original bias std. error
t1* 0.7183433 0.002164339 0.06513426

Aus den Ergebnissen können wir sehen:

• Das geschätzte R-Quadrat für dieses Regressionsmodell beträgt 0,7183433 .
• Der Standardfehler für diese Schätzung beträgt 0,06513426 .

Wir können die Verteilung der Bootstrapping-Beispiele auch schnell visualisieren:

 plot(reps)

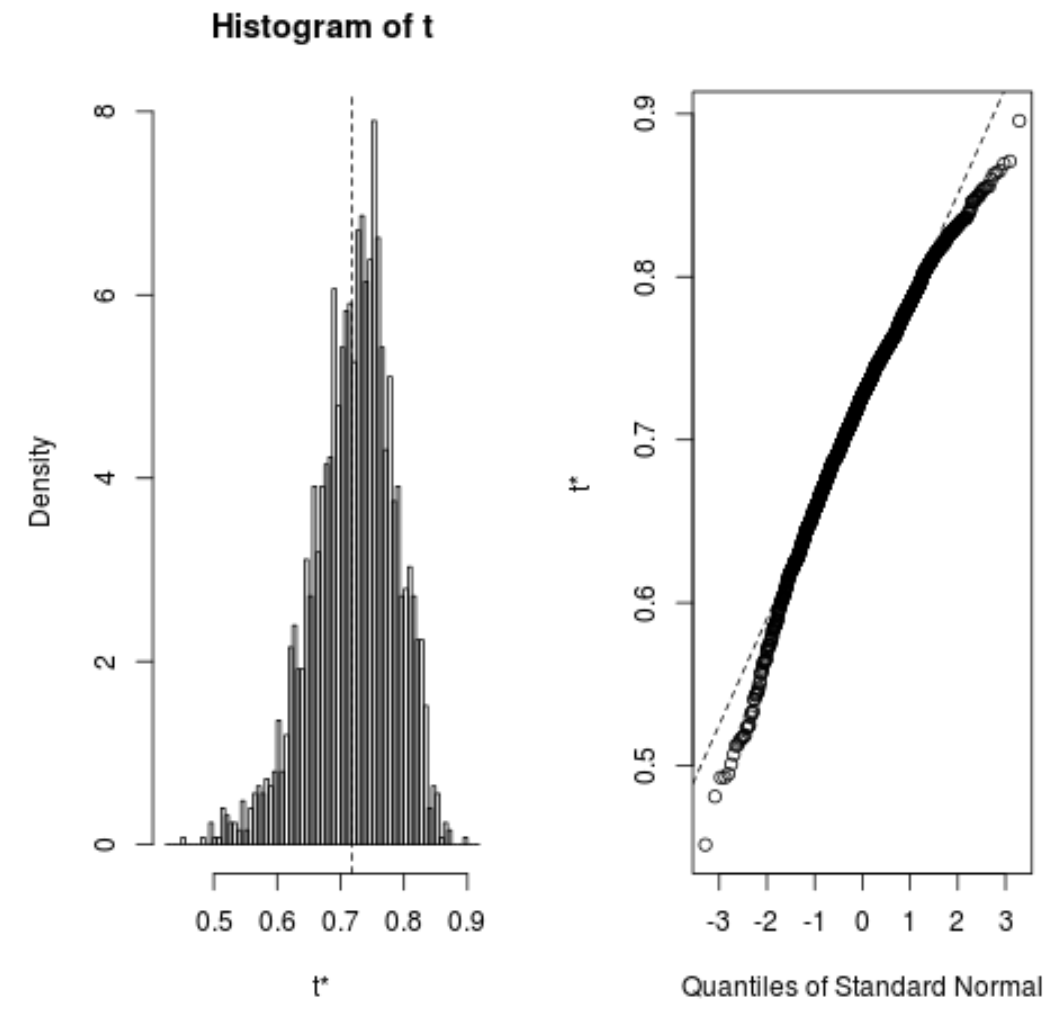
Wir können auch den folgenden Code verwenden, um das 95 %-Konfidenzintervall für das geschätzte R-Quadrat des Modells zu berechnen:

 #calculate adjusted bootstrap percentile (BCa) interval
boot.ci(reps, type=" bca ")

CALL: 
boot.ci(boot.out = reps, type = "bca")

Intervals: 
Level BCa          
95% (0.5350, 0.8188)  
Calculations and Intervals on Original Scale

Aus dem Ergebnis können wir ersehen, dass das Bootstrapping-Konfidenzintervall von 95 % für die wahren R-Quadrat-Werte (0,5350, 0,8188) beträgt.

Beispiel 2: Bootstrap mehrerer Statistiken

Der folgende Code zeigt, wie der Standardfehler für jeden Koeffizienten in einem multiplen linearen Regressionsmodell berechnet wird:

 set.seed(0)
library (boot)

#define function to calculate fitted regression coefficients
coef_function <- function (formula, data, indices) {
  d <- data[indices,] #allows boot to select sample
  fit <- lm(formula, data=d) #fit regression model
  return (coef(fit)) #return coefficient estimates of model
}

#perform bootstrapping with 2000 replications
reps <- boot(data=mtcars, statistic=coef_function, R=2000, formula=mpg~disp)

#view results of boostrapping
reps

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = mtcars, statistic = coef_function, R = 2000, formula = mpg ~ 
    available)


Bootstrap Statistics:
       original bias std. error
t1* 29.59985476 -5.058601e-02 1.49354577
t2* -0.04121512 6.549384e-05 0.00527082

Aus den Ergebnissen können wir sehen:

• Der geschätzte Koeffizient für den Modellabschnitt beträgt 29,59985476 und der Standardfehler dieser Schätzung beträgt 1,49354577 .
• Der geschätzte Koeffizient für die Prädiktorvariable disp im Modell beträgt -0,04121512 und der Standardfehler dieser Schätzung beträgt 0,00527082 .

Wir können die Verteilung der Bootstrapping-Beispiele auch schnell visualisieren:

 plot(reps, index=1) #intercept of model
plot(reps, index=2) #disp predictor variable

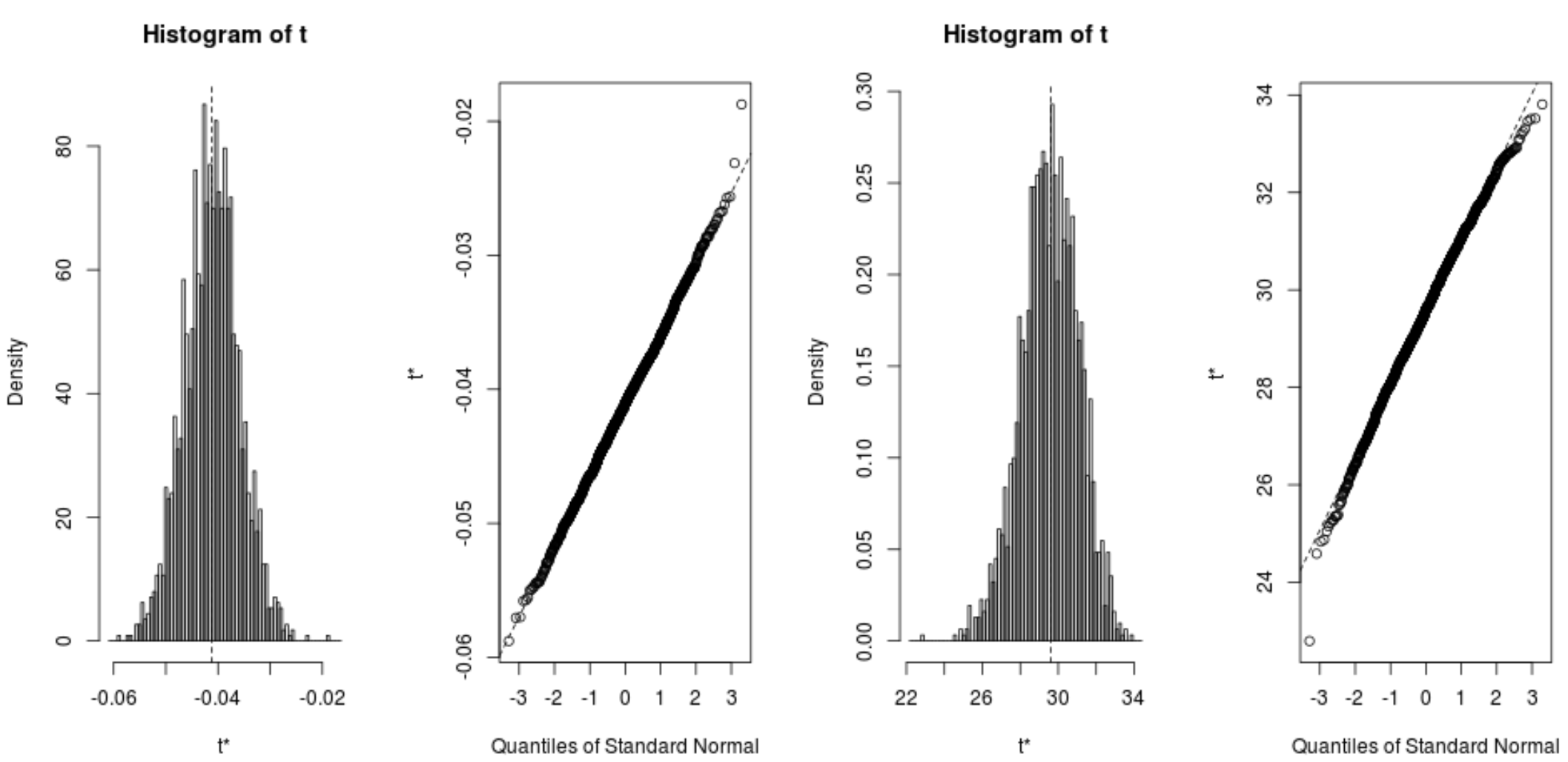
Wir können auch den folgenden Code verwenden, um die 95 %-Konfidenzintervalle für jeden Koeffizienten zu berechnen:

 #calculate adjusted bootstrap percentile (BCa) intervals
boot.ci(reps, type=" bca ", index=1) #intercept of model
boot.ci(reps, type=" bca ", index=2) #disp predictor variable

CALL: 
boot.ci(boot.out = reps, type = "bca", index = 1)

Intervals: 
Level BCa          
95% (26.78, 32.66)  
Calculations and Intervals on Original Scale
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 2000 bootstrap replicates

CALL: 
boot.ci(boot.out = reps, type = "bca", index = 2)

Intervals: 
Level BCa          
95% (-0.0520, -0.0312)  
Calculations and Intervals on Original Scale

Aus den Ergebnissen können wir ersehen, dass die Bootstrapping-95-%-Konfidenzintervalle für die Modellkoeffizienten wie folgt lauten:

• IC zum Abfangen: (26,78, 32,66)
• CI für Disp : (-.0520, -.0312)

Zusätzliche Ressourcen

So führen Sie eine einfache lineare Regression in R durch
So führen Sie eine multiple lineare Regression in R durch
Einführung in Konfidenzintervalle