So führen sie eine box-cox-transformation in r durch (mit beispielen)

Eine Box-Cox-Transformation ist eine häufig verwendete Methode zur Transformation eines nicht normalverteilten Datensatzes in einennormalverteilteren Satz.

Die Grundidee dieser Methode besteht darin, mithilfe der folgenden Formel einen Wert für λ zu finden, sodass die transformierten Daten möglichst nahe an der Normalverteilung liegen:

• y(λ) = (y ^λ – 1) / λ wenn y ≠ 0
• y(λ) = log(y) wenn y = 0

Wir können eine Box-Cox-Transformation in R mit der Funktion boxcox() aus der MASS()- Bibliothek durchführen. Das folgende Beispiel zeigt, wie Sie diese Funktion in der Praxis nutzen können.

Eine schöne Zusammenfassung der Entwicklung der Box-Cox-Transformation finden Sie in diesem Artikel der University of Connecticut.

Beispiel: Box-Cox-Transformation in R

Der folgende Code zeigt, wie Sie ein lineares Regressionsmodell an einen Datensatz anpassen und dann mit der Funktion boxcox() ein optimales Lambda finden, um die Antwortvariable zu transformieren und ein neues Modell anzupassen.

 library (MASS)

#create data
y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8)
x=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8)

#fit linear regression model
model <- lm(y~x)

#find optimal lambda for Box-Cox transformation 
bc <- boxcox(y ~ x)
(lambda <- bc$x[which.max(bc$y)])

[1] -0.4242424

#fit new linear regression model using the Box-Cox transformation
new_model <- lm(((y^lambda-1)/lambda) ~ x)

Das optimale Lambda lag bei -0,4242424 . Daher ersetzte das neue Regressionsmodell die ursprüngliche Antwortvariable y durch die Variable y = (y ^-0,4242424 – 1) / -0,4242424.

Der folgende Code zeigt, wie zwei QQ-Diagramme in R erstellt werden, um die Unterschiede in den Residuen zwischen den beiden Regressionsmodellen zu visualisieren:

 #define plotting area
op <- par(pty = "s", mfrow = c(1, 2))

#QQ plot for original model
qqnorm(model$residuals)
qqline(model$residuals)

#QQ plot for Box-Cox transformed model
qqnorm(new_model$residuals)
qqline(new_model$residuals)

#display both QQ plots
by(op)

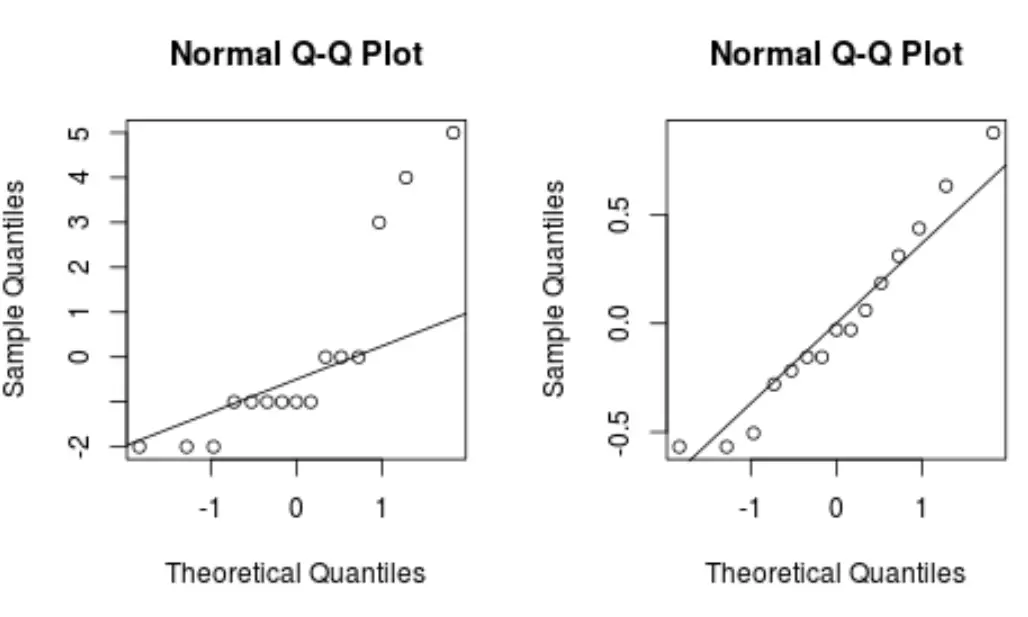
Wenn die Datenpunkte in einem QQ-Diagramm entlang einer geraden diagonalen Linie liegen, folgt der Datensatz im Allgemeinen wahrscheinlich einer Normalverteilung.

Beachten Sie, dass das Box-Cox-transformierte Modell ein QQ-Diagramm mit einer viel geraderen Linie als das ursprüngliche Regressionsmodell erzeugt.

Dies weist darauf hin, dass die Residuen des Box-Cox-transformierten Modells viel normaler verteilt sind, was eine der Annahmen der linearen Regression erfüllt.

Zusätzliche Ressourcen

So transformieren Sie Daten in R (Log, Quadratwurzel, Kubikwurzel)
So erstellen und interpretieren Sie ein QQ-Diagramm in R
So führen Sie einen Shapiro-Wilk-Test auf Normalität in R durch