So führen sie eine box-cox-transformation in python durch

Eine Box-Cox-Transformation ist eine häufig verwendete Methode zur Transformation eines nicht normalverteilten Datensatzes in einennormalverteilteren Satz.

Die Grundidee dieser Methode besteht darin, mithilfe der folgenden Formel einen Wert für λ zu finden, sodass die transformierten Daten möglichst nahe an der Normalverteilung liegen:

• y(λ) = (y ^λ – 1) / λ wenn y ≠ 0
• y(λ) = log(y) wenn y = 0

Mit der Funktion scipy.stats.boxcox() können wir eine Box-Cox-Transformation in Python durchführen.

Das folgende Beispiel zeigt, wie Sie diese Funktion in der Praxis nutzen können.

Beispiel: Box-Cox-Transformation in Python

Angenommen, wir generieren eine zufällige Menge von 1000 Werten aus einer Exponentialverteilung :

 #load necessary packages
import numpy as np 
from scipy. stats import boxcox 
import seaborn as sns 

#make this example reproducible
n.p. random . seeds (0)

#generate dataset
data = np. random . exponential (size= 1000 )

#plot the distribution of data values
sns. distplot (data, hist= False , kde= True ) 

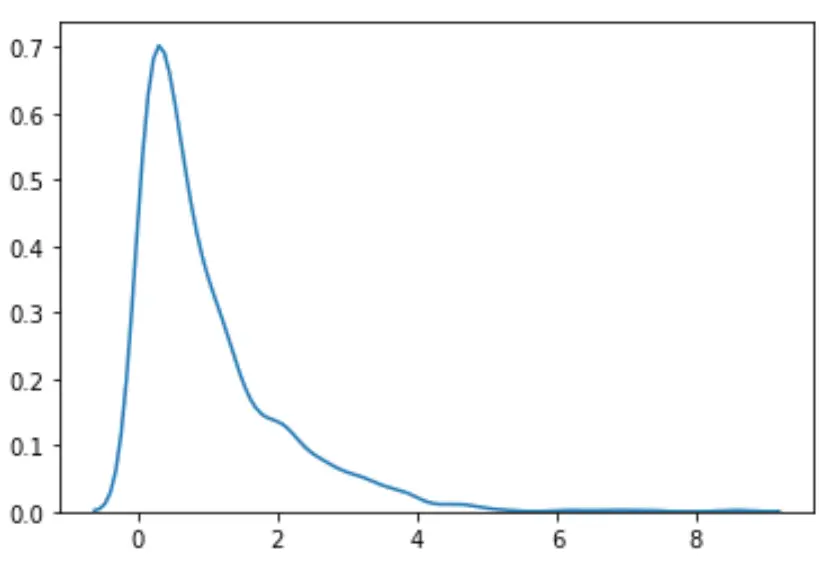
Wir können sehen, dass die Verteilung nicht normal erscheint.

Wir können die Funktion boxcox() verwenden, um einen optimalen Lambdawert zu finden, der eine normalere Verteilung erzeugt:

 #perform Box-Cox transformation on original data
transformed_data, best_lambda = boxcox(data) 

#plot the distribution of the transformed data values
sns. distplot (transformed_data, hist= False , kde= True ) 

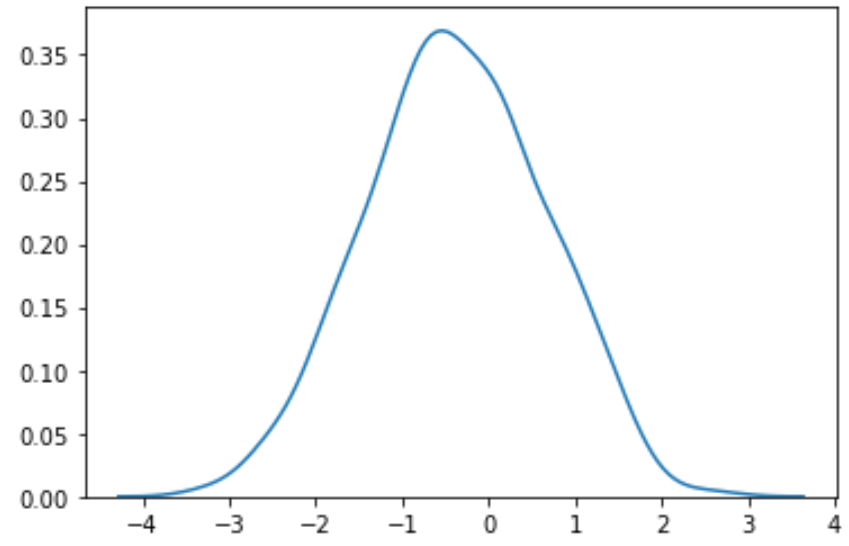
Wir können sehen, dass die transformierten Daten einer viel normaleren Verteilung folgen.

Wir können auch den genauen Lambda-Wert ermitteln, der zur Durchführung der Box-Cox-Transformation verwendet wird:

 #display optimal lambda value
print (best_lambda)

0.2420131978174143

Der optimale Lambda-Wert lag bei etwa 0,242 .

Daher wurde jeder Datenwert mithilfe der folgenden Gleichung transformiert:

Neu = (alt ^0,242 – 1) / 0,242

Wir können dies bestätigen, indem wir die Werte der Originaldaten im Vergleich zu den transformierten Daten betrachten:

 #view first five values of original dataset
data[0:5]

array([0.79587451, 1.25593076, 0.92322315, 0.78720115, 0.55104849])

#view first five values of transformed dataset
transformed_data[0:5]

array([-0.22212062, 0.23427768, -0.07911706, -0.23247555, -0.55495228])

Der erste Wert im Originaldatensatz war 0,79587 . Daher haben wir die folgende Formel angewendet, um diesen Wert umzuwandeln:

Neu = (.79587 ^0,242 – 1) / 0,242 = -0,222

Wir können bestätigen, dass der erste Wert im transformierten Datensatz tatsächlich -0,222 ist.

Zusätzliche Ressourcen

So erstellen und interpretieren Sie ein QQ-Diagramm in Python
So führen Sie einen Shapiro-Wilk-Normalitätstest in Python durch