Box- und whisker-plot
In diesem Artikel wird erklärt, was ein Boxplot, auch Boxplot (oder Boxplot) genannt, ist. Sie erfahren, wie diese Art von statistischen Diagrammen erstellt werden, und erfahren eine gelöste Übung zu einem Box-and-Whisker-Diagramm und seiner Interpretation.
Was ist ein Box-and-Whisker-Plot?
Der Boxplot , auch Boxplot oder Boxplot genannt, ist ein Diagramm, das einen Satz statistischer Daten mithilfe von Quartilen visuell darstellt.
Das Hauptmerkmal des Box- und Whisker-Diagramms besteht darin, dass Sie die Streuung einer Datenreihe schnell visualisieren können, da es die Quartile, den Median, die Extremwerte und die Ausreißer der Daten anzeigt.
Somit besteht diese Art von Diagramm aus einem rechteckigen Kasten und einigen Linien (oder Whiskern), aus denen die folgenden Werte hervorgehen:
- Die Grenzen der Box geben das erste und dritte Quartil (Q 1 und Q 3 ) an. Und die vertikale Linie innerhalb der Box ist der Median (entspricht dem zweiten Quartil Q2 ).
- Die Grenzen der Whisker (oder Arme) sind die Extremwerte , also der Minimalwert und der Maximalwert der Datenreihe.
- Bei den Punkten außerhalb der Whiskers handelt es sich um Ausreißer , also Daten, die wahrscheinlich falsch gemessen wurden und daher in der statistischen Untersuchung nicht berücksichtigt werden sollten.
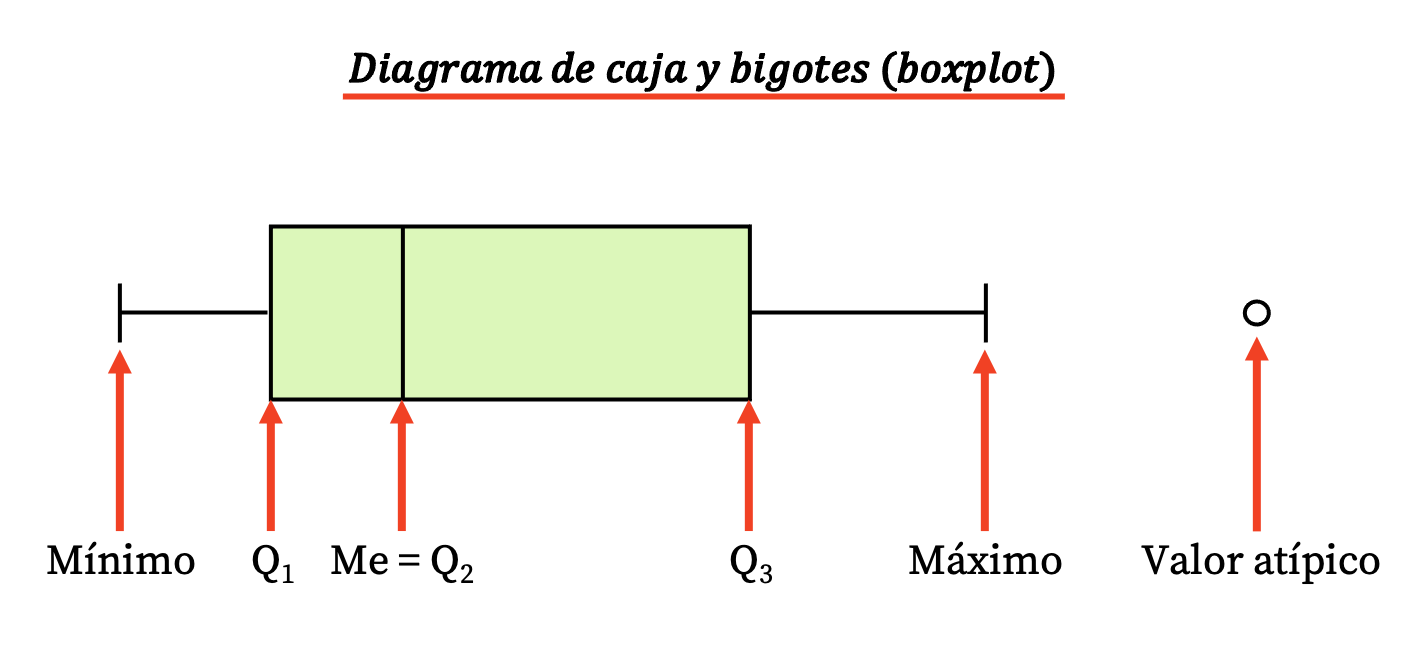
Beachten Sie, dass der Unterschied zwischen dem dritten und dem ersten Quartil der Interquartilbereich (oder Interquartilbereich) ist, ein weiteres Maß für die statistische Streuung.
Box- und Whisker-Plots sind sehr nützlich für den Vergleich numerischer Variablen. Es eignet sich jedoch nicht zur Darstellung kategorialer Variablen.
So erstellen Sie ein Box- und Whisker-Diagramm
Um einen Box-and-Whisker-Plot (oder Boxplot) aus einer Datenreihe zu erstellen, müssen die folgenden Schritte ausgeführt werden:
- Sortieren Sie die statistischen Datenbeispiele.
- Berechnen Sie die Quartile (Q 1 , Q 2 und Q 3 ) und stellen Sie sie als Kästchen im Diagramm dar. Das erste und dritte Quartil entsprechen den Grenzen des Kästchens. Um den Median (das zweite Quartil) darzustellen, müssen Sie eine Linie innerhalb des Kästchens zeichnen, wo sich sein Wert befindet.
- Berechnen Sie den Interquartilbereich, der dem dritten Quartil minus dem ersten Quartil entspricht.
- Berechnen Sie die zulässigen Werte LI und LS, deren Formeln lauten:
- Identifizieren Sie Stichprobenausreißer, bei denen es sich um Werte handelt, die kleiner als LI oder größer als LS sind. Stellen Sie diese Werte außerhalb des Whisker-Bereichs mit Punkten dar.
- Identifizieren und stellen Sie die Extremwerte dar, bei denen es sich um den kleinsten und den größten Wert im von LI und LS gebildeten Intervall handelt. Diese Werte stellen das Ende der beiden Whiskers im Diagramm dar.
![]()
![]()
![]()
Beispiel für ein Box- und Whisker-Diagramm
In Anbetracht der Definition und Theorie des Box- und Whisker-Plots (oder Boxplots) finden Sie unten ein konkretes Beispiel, um das Konzept besser zu verstehen und zu sehen, wie diese Art von statistischem Plot ausgeführt wird.
- Zeichnen Sie ein Boxplot des folgenden statistischen Datensatzes.

In diesem Fall sind die Daten bereits vom kleinsten zum größten sortiert, sodass keine Änderungen erforderlich sind. Andernfalls sollten wir zuerst die Beispieldaten sortieren.
Zweitens extrahieren wir die Quartile der Stichprobe:
![]()
![]()
![]()
Nachdem wir die drei Quartile berechnet haben, ermitteln wir den Interquartilbereich, indem wir Quartil 3 minus Quartil 1 subtrahieren:
![]()
Wir berechnen nun die LI- und LS-Grenzwerte, das sind die Werte, ab denen Daten als atypisch gelten. Dazu müssen Sie die folgenden Formeln verwenden:
![]()
![]()
In diesem Fall haben wir also zwei Ausreißer, denn 3,02 ist kleiner als 3,16 und 5,71 ist größer als 5,56.
![]()
Schließlich müssen noch die Extremwerte identifiziert werden, die das Minimum und Maximum aller Daten im Intervall [LI,LS] darstellen. Daher beträgt in unserem Beispiel der Minimalwert 3,70 und der Maximalwert 4,81.
![]()
![]()
Nachdem wir also alle Werte der Box und des Whisker-Plots identifiziert haben, müssen wir nur noch die grafische Darstellung erstellen:
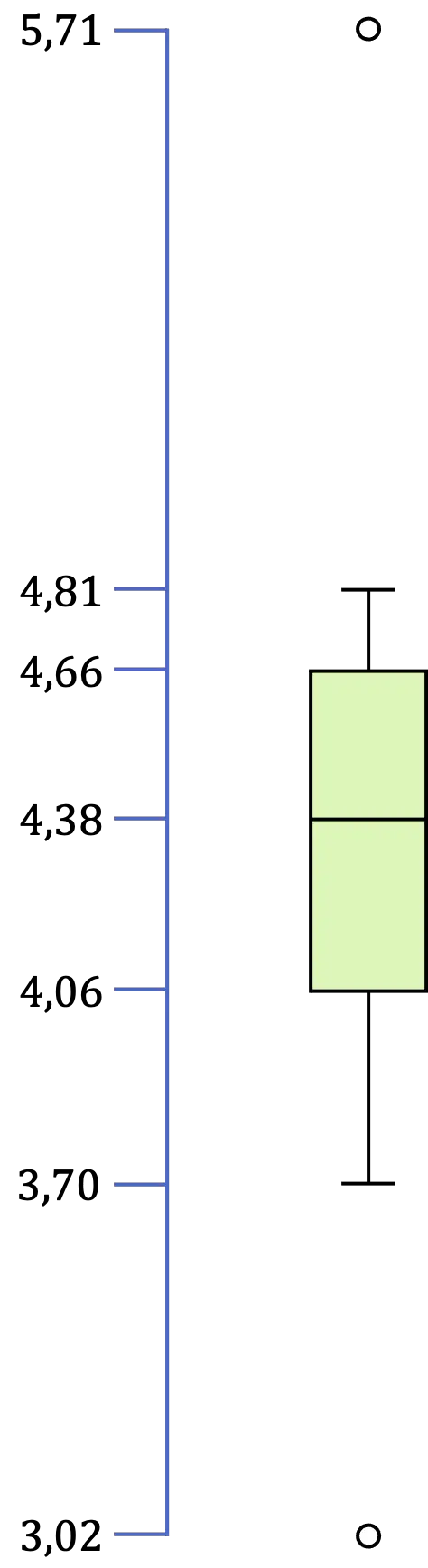
Wofür wird ein Box-and-Whisker-Diagramm verwendet?
Lassen Sie uns abschließend sehen, wozu es dient und wie der Box- und Whisker-Plot (oder Boxplot) zu interpretieren ist.
Offensichtlich ist das Box-and-Whisker-Diagramm sehr nützlich, um schnell die Quartile, den Interquartilbereich, den Median, die Extremwerte und Ausreißer einer Datenreihe zu ermitteln, da alle diese statistischen Maße mit einem einfachen Blick identifiziert werden können.
Darüber hinaus wird das Box-and-Whisker-Plot zur Analyse der Symmetrie der statistischen Stichprobe verwendet, da es den gesamten Datensatz visuell darstellt. Wenn der Median nicht in der Mitte der Box liegt, bedeutet dies, dass die Stichprobe nicht symmetrisch ist.
In ähnlicher Weise werden Boxplots an der Börse häufig verwendet, um die Schwankungen des Aktienkurses über einen bestimmten Zeitraum darzustellen, da sie es ermöglichen, den Maximalwert, den Minimalwert und die Zwischenwerte in einem kurzen Zeitraum zu sehen. Zeit und treffen so schnellere Entscheidungen.